
Digital Signature Algorithm
Encyclopedia
The Digital Signature Algorithm (DSA) is a United States Federal Government
standard
or FIPS
for digital signature
s. It was proposed by the National Institute of Standards and Technology
(NIST) in August 1991 for use in their Digital Signature Standard (DSS), specified in FIPS
186, adopted in 1993. A minor revision was issued in 1996 as FIPS 186-1. The standard was expanded further in 2000 as FIPS 186-2 and again in 2009 as FIPS 186-3.
DSA is covered by , filed July 26, 1991, and attributed to David W. Kravitz, a former NSA
employee. This patent was given to "The United States of America as represented by the Secretary of Commerce, Washington, D.C." and the NIST has made this patent available worldwide royalty
-free. Dr. Claus P. Schnorr
claims that his (expired) covered DSA; this claim is disputed. DSA is a variant of the ElGamal Signature Scheme
.
The algorithm parameters (p, q, g) may be shared between different users of the system.
There exist efficient algorithms for computing the modular exponentiation
s h(p–1)/q mod p and gx mod p, such as exponentiation by squaring
.
The first two steps amount to creating a new per-user key. The modular exponentiation here is the most computationally expensive part of the signing operation, and it may be computed before the message hash is known.
The modular inverse k−1 mod q is the second most expensive part, and it may also be computed before the message hash is known. It may be computed using the extended Euclidean algorithm
or using Fermat's little theorem
as kq−2 mod q.
DSA is similar to the ElGamal signature scheme
.
First, if g = h(p − 1)/q mod p it follows that
gq ≡ hp − 1 ≡ 1 (mod p) by
Fermat's little theorem
. Since g > 1 and q is prime, g must have order q.
The signer computes

Thus

Since g has order q (mod p) we have

Finally, the correctness of DSA follows from
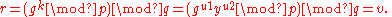
Federal government of the United States
The federal government of the United States is the national government of the constitutional republic of fifty states that is the United States of America. The federal government comprises three distinct branches of government: a legislative, an executive and a judiciary. These branches and...
standard
Federal Information Processing Standard
A Federal Information Processing Standard is a publicly announced standardization developed by the United States federal government for use in computer systems by all non-military government agencies and by government contractors, when properly invoked and tailored on a contract...
or FIPS
Federal Information Processing Standard
A Federal Information Processing Standard is a publicly announced standardization developed by the United States federal government for use in computer systems by all non-military government agencies and by government contractors, when properly invoked and tailored on a contract...
for digital signature
Digital signature
A digital signature or digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, and that it was not altered in transit...
s. It was proposed by the National Institute of Standards and Technology
National Institute of Standards and Technology
The National Institute of Standards and Technology , known between 1901 and 1988 as the National Bureau of Standards , is a measurement standards laboratory, otherwise known as a National Metrological Institute , which is a non-regulatory agency of the United States Department of Commerce...
(NIST) in August 1991 for use in their Digital Signature Standard (DSS), specified in FIPS
Federal Information Processing Standard
A Federal Information Processing Standard is a publicly announced standardization developed by the United States federal government for use in computer systems by all non-military government agencies and by government contractors, when properly invoked and tailored on a contract...
186, adopted in 1993. A minor revision was issued in 1996 as FIPS 186-1. The standard was expanded further in 2000 as FIPS 186-2 and again in 2009 as FIPS 186-3.
DSA is covered by , filed July 26, 1991, and attributed to David W. Kravitz, a former NSA
National Security Agency
The National Security Agency/Central Security Service is a cryptologic intelligence agency of the United States Department of Defense responsible for the collection and analysis of foreign communications and foreign signals intelligence, as well as protecting U.S...
employee. This patent was given to "The United States of America as represented by the Secretary of Commerce, Washington, D.C." and the NIST has made this patent available worldwide royalty
Royalties
Royalties are usage-based payments made by one party to another for the right to ongoing use of an asset, sometimes an intellectual property...
-free. Dr. Claus P. Schnorr
Claus P. Schnorr
Claus-Peter Schnorr is a distinguished German mathematician and cryptographer. He received his Ph.D. from the University of Saarbrücken in 1966, and his habilitation in 1970. Schnorr's contributions to cryptography include his study of Schnorr groups, which are used in the digital signature...
claims that his (expired) covered DSA; this claim is disputed. DSA is a variant of the ElGamal Signature Scheme
ElGamal signature scheme
The ElGamal signature scheme is a digital signature scheme which is based on the difficulty of computing discrete logarithms. It was described by Taher ElGamal in 1984....
.
Key generation
Key generation has two phases. The first phase is a choice of algorithm parameters which may be shared between different users of the system, while the second phase computes public and private keys for a single user.Parameter generation
- Choose an approved cryptographic hash functionCryptographic hash functionA cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
H. In the original DSS, H was always SHA-1, but the stronger SHA-2SHA-2In cryptography, SHA-2 is a set of cryptographic hash functions designed by the National Security Agency and published in 2001 by the NIST as a U.S. Federal Information Processing Standard. SHA stands for Secure Hash Algorithm. SHA-2 includes a significant number of changes from its predecessor,...
hash functions are approved for use in the current DSS. The hash output may be truncated to the size of a key pair. - Decide on a key length L and N. This is the primary measure of the cryptographic strength of the key. The original DSS constrained L to be a multiple of 64 between 512 and 1024 (inclusive). NIST 800-57 recommends lengths of 2048 (or 3072) for keys with security lifetimes extending beyond 2010 (or 2030), using correspondingly longer N. FIPS 186-3 specifies L and N length pairs of (1024,160), (2048,224), (2048,256), and (3072,256).
- Choose an N-bit prime q. N must be less than or equal to the hash output length.
- Choose an L-bit prime modulus p such that p–1 is a multiple of q.
- Choose g, a number whose multiplicative order modulo p is q. This may be done by setting g = h(p–1)/q mod p for some arbitrary h (1 < h < p−1), and trying again with a different h if the result comes out as 1. Most choices of h will lead to a usable g; commonly h=2 is used.
The algorithm parameters (p, q, g) may be shared between different users of the system.
Per-user keys
Given a set of parameters, the second phase computes private and public keys for a single user:- Choose x by some random method, where 0 < x < q.
- Calculate y = gx mod p.
- Public key is (p, q, g, y). Private key is x.
There exist efficient algorithms for computing the modular exponentiation
Modular exponentiation
Modular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography....
s h(p–1)/q mod p and gx mod p, such as exponentiation by squaring
Exponentiation by squaring
Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
.
Signing
Let H be the hashing function and m the message:- Generate a random per-message value k where 0 < k < q
- Calculate r = (gk mod p) mod q
- In the unlikely case that r = 0, start again with a different random k
- Calculate s = (k−1(H(m) + x·r)) mod q
- In the unlikely case that s = 0, start again with a different random k
- The signature is (r, s)
The first two steps amount to creating a new per-user key. The modular exponentiation here is the most computationally expensive part of the signing operation, and it may be computed before the message hash is known.
The modular inverse k−1 mod q is the second most expensive part, and it may also be computed before the message hash is known. It may be computed using the extended Euclidean algorithm
Extended Euclidean algorithm
The extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the greatest common divisor of integers a and b, as the Euclidean algorithm does, it also finds integers x and y that satisfy Bézout's identityThe extended Euclidean algorithm is particularly useful when a...
or using Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
as kq−2 mod q.
Verifying
- Reject the signature if 0 < r < q or 0 < s < q is not satisfied.
- Calculate w = s−1 mod q
- Calculate u1 = H(m)·w mod q
- Calculate u2 = r·w mod q
- Calculate v = ((gu1·yu2) mod p) mod q
- The signature is valid if v = r
DSA is similar to the ElGamal signature scheme
ElGamal signature scheme
The ElGamal signature scheme is a digital signature scheme which is based on the difficulty of computing discrete logarithms. It was described by Taher ElGamal in 1984....
.
Correctness of the algorithm
The signature scheme is correct in the sense that the verifier will always accept genuine signatures. This can be shown as follows:First, if g = h(p − 1)/q mod p it follows that
gq ≡ hp − 1 ≡ 1 (mod p) by
Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
. Since g > 1 and q is prime, g must have order q.
The signer computes

Thus

Since g has order q (mod p) we have

Finally, the correctness of DSA follows from
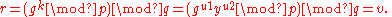
Sensitivity
With DSA, the entropy, secrecy and uniqueness of the random signature value k is critical. It is so critical that violating any one of those three requirements can reveal your entire private key to an attacker. Using the same value twice (even while keeping k secret), using a predictable value, or leaking even a few bits of k in each of several signatures, is enough to break DSA.External links
- FIPS-186, the first version of the official DSA specification.
- FIPS-186, change notice No.1, the first change notice to the first version of the specification.
- FIPS-186-1, the first revision to the official DSA specification.
- FIPS-186-3, the third and current revision to the official DSA specification.
- FIPS-186-3 Approval, Approval announcement of the third revision to the official DSA specification.
- Recommendation for Key Management -- Part 1: general, NIST Special Publication 800-57, p. 62–63

