Index calculus algorithm
Encyclopedia
In group theory
, the index calculus algorithm is a probabilistic algorithm
for computing discrete logarithm
s.
It relies on finding a relatively small factor base
, for which most elements of the group can be expressed as products of elements in the factor base. Suitable techniques are known for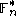
, the multiplicative group of a finite field
of order n. When n = 2m, the index-calculus algorithm is the best solution known for computing discrete logarithms. For n prime, a modification based on the general number field sieve
provides better asymptotic performance.
problem asks us to find an x such that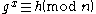
, where g, h, and the modulus n are given.
The algorithm (described in detail below) applies to the group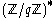
where q is prime. It requires a factor base as input. This factor base is usually chosen to be the number −1 and the first r primes starting with 2. From the point of view of efficiency, we want this factor base to be small, but in order to solve the discrete log for a large group we require the factor base to be (relatively) large. In practical implementations of the algorithm, those conflicting objectives are compromised one way or another.
It is noteworthy that the lack of the notion of prime elements in the group of points on elliptic curves, makes it impossible to find an efficient factor base to run index calculus in these groups. Therefore this algorithm is incapable of solving discrete logarithms efficiently in elliptic curve groups.
The algorithm is performed in three stages. The first two stages depend only on the generator g and prime modulus q, and find the discrete logarithms of a factor base of r small primes. The third stage finds the discrete log of the desired number h in terms of the discrete logs of the factor base.
The first stage consists of searching for a set of r linearly independent relations between the factor base and power of the generator
g. Each relation contributes one equation to a system of linear equations in r unknowns, namely the discrete logarithms of the r primes in the factor base. This stage is embarrassingly parallel
and easy to divide among many computers.
The second stage solves the system of linear equations to compute the discrete logs of the factor base. Although a minor computation compared to the other stages, a system of hundreds of thousands or millions of equations is a significant computation requiring large amounts of memory, and it is not embarrassingly parallel, so a supercomputer
is typically used.
The third stage searches for a power s of the generator g which, when multiplied by the argument h, may be factored in terms of the factor base gsh = (−1)f0 2f1 3f2···prfr.
Finally, in an operation too simple to really be called a fourth stage, the results of the second and third stages can be rearranged by simple algebraic manipulation to work out the desired discrete logarithm x = f0logg(−1) + f1logg2 + f2logg3 + ··· + frloggpr − s.
The first and third stages are both embarrassingly parallel, and in fact the third stage does not depend on the results of the first two stages, so it may be done in parallel with them.
The choice of the factor base size r is critical, and the details are too intricate to explain here. The larger the factor base, the easier it is to find relations in stage 1, and the easier it is to complete stage 3, but the more relations you need before you can proceed to stage 2, and the more difficult stage 2 is. The relative availability of computers suitable for the different types of computation required for stages 1 and 2 is also important.
Output: x such that gx ≡ h (mod q).
) of the index-calculus algorithm can be stated as
.
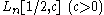For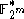
, an optimization by Don Coppersmith
yields an algorithm with an expected running time of
.
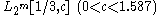became important in 1976 with the creation of the Diffie-Hellman cryptosystem, R. Merkle from Stanford University rediscovered the idea in 1977. The first publications came in the next two years from Merkle's colleagues,. Finally, Adleman
optimized the algorithm and presented it in the form we know it today.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the index calculus algorithm is a probabilistic algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for computing discrete logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
s.
It relies on finding a relatively small factor base
Factor base
In computational number theory, the factor base is a mathematical tool commonly used in algorithms involving extensive sieving of potential factors.-Usage:...
, for which most elements of the group can be expressed as products of elements in the factor base. Suitable techniques are known for
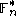, the multiplicative group of a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
of order n. When n = 2m, the index-calculus algorithm is the best solution known for computing discrete logarithms. For n prime, a modification based on the general number field sieve
General number field sieve
In number theory, the general number field sieve is the most efficient classical algorithm known for factoring integers larger than 100 digits...
provides better asymptotic performance.
Description
Roughly speaking, the discrete logDiscrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
problem asks us to find an x such that
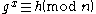, where g, h, and the modulus n are given.The algorithm (described in detail below) applies to the group
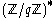where q is prime. It requires a factor base as input. This factor base is usually chosen to be the number −1 and the first r primes starting with 2. From the point of view of efficiency, we want this factor base to be small, but in order to solve the discrete log for a large group we require the factor base to be (relatively) large. In practical implementations of the algorithm, those conflicting objectives are compromised one way or another.It is noteworthy that the lack of the notion of prime elements in the group of points on elliptic curves, makes it impossible to find an efficient factor base to run index calculus in these groups. Therefore this algorithm is incapable of solving discrete logarithms efficiently in elliptic curve groups.
The algorithm is performed in three stages. The first two stages depend only on the generator g and prime modulus q, and find the discrete logarithms of a factor base of r small primes. The third stage finds the discrete log of the desired number h in terms of the discrete logs of the factor base.
The first stage consists of searching for a set of r linearly independent relations between the factor base and power of the generator
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
g. Each relation contributes one equation to a system of linear equations in r unknowns, namely the discrete logarithms of the r primes in the factor base. This stage is embarrassingly parallel
Embarrassingly parallel
In parallel computing, an embarrassingly parallel workload is one for which little or no effort is required to separate the problem into a number of parallel tasks...
and easy to divide among many computers.
The second stage solves the system of linear equations to compute the discrete logs of the factor base. Although a minor computation compared to the other stages, a system of hundreds of thousands or millions of equations is a significant computation requiring large amounts of memory, and it is not embarrassingly parallel, so a supercomputer
Supercomputer
A supercomputer is a computer at the frontline of current processing capacity, particularly speed of calculation.Supercomputers are used for highly calculation-intensive tasks such as problems including quantum physics, weather forecasting, climate research, molecular modeling A supercomputer is a...
is typically used.
The third stage searches for a power s of the generator g which, when multiplied by the argument h, may be factored in terms of the factor base gsh = (−1)f0 2f1 3f2···prfr.
Finally, in an operation too simple to really be called a fourth stage, the results of the second and third stages can be rearranged by simple algebraic manipulation to work out the desired discrete logarithm x = f0logg(−1) + f1logg2 + f2logg3 + ··· + frloggpr − s.
The first and third stages are both embarrassingly parallel, and in fact the third stage does not depend on the results of the first two stages, so it may be done in parallel with them.
The choice of the factor base size r is critical, and the details are too intricate to explain here. The larger the factor base, the easier it is to find relations in stage 1, and the easier it is to complete stage 3, but the more relations you need before you can proceed to stage 2, and the more difficult stage 2 is. The relative availability of computers suitable for the different types of computation required for stages 1 and 2 is also important.
The algorithm
Input: Discrete logarithm generator g, modulus q and argument h. Factor base {−1,2,3,5,7,11,...,pr}, of length r+1.Output: x such that gx ≡ h (mod q).
- relations ← empty_list
- for k = 1, 2, ...
- Using an integer factorizationInteger factorizationIn number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
algorithm optimized for smooth numbers, try to factor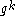
modulo q using the factor base, i.e. find 
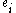's such that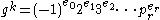 
- Each time a factorization is found:
- Store k and the computed
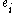's as a vector 
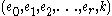(this is a called a relation) - If this relation is linearly independent to the other relations:
- Add it to the list of relations
- If there are at least r+1 relations, exit loop
- Store k and the computed
- Using an integer factorization
- Form a matrix whose rows are the relations
- Obtain the reduced echelon form of the matrix
- The first element in the last column is the discrete log of −1 and the second element is the discrete log of 2 and so on
- for s = 0, 1, 2, ...
- Try to factor
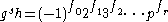over the factor base - When a factorization is found:
- Output
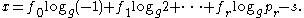
- Output
- Try to factor
Complexity
Assuming an optimal selection of the factor base, the expected running time (using L-notationL-notation
L-notation is an asymptotic notation analogous to big-O notation, denoted as L_n[\alpha,c] for a bound variable n tending to infinity. Like big-O notation, it is usually used to roughly convey the computational complexity of a particular algorithm....
) of the index-calculus algorithm can be stated as
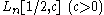.For
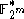, an optimization by Don CoppersmithDon Coppersmith
Don Coppersmith is a cryptographer and mathematician. He was involved in the design of the Data Encryption Standard block cipher at IBM, particularly the design of the S-boxes, strengthening them against differential cryptanalysis...
yields an algorithm with an expected running time of
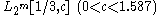.History
The first to discover the idea was Kraitchik in 1922. After DLPDiscrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
became important in 1976 with the creation of the Diffie-Hellman cryptosystem, R. Merkle from Stanford University rediscovered the idea in 1977. The first publications came in the next two years from Merkle's colleagues,. Finally, Adleman
Leonard Adleman
Leonard Max Adleman is an American theoretical computer scientist and professor of computer science and molecular biology at the University of Southern California. He is known for being a co-inventor of the RSA cryptosystem in 1977, and of DNA computing...
optimized the algorithm and presented it in the form we know it today.
External links
- Discrete logarithms in finite fields and their cryptographic significance, by Andrew OdlyzkoAndrew OdlyzkoAndrew Michael Odlyzko is a mathematician and a former head of the University of Minnesota's Digital Technology Center.In the field of mathematics he has published extensively on analytic number theory, computational number theory, cryptography, algorithms and computational complexity,...
- Discrete Logarithm Problem, by Chris Studholme, including the June 21, 2002 paper "The Discrete Log Problem".