L-notation
Encyclopedia
L-notation is an asymptotic
notation analogous to big-O notation, denoted as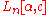
for a bound variable 
tending to infinity
. Like big-O notation, it is usually used to roughly convey the computational complexity
of a particular algorithm
.
It is defined as
,
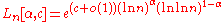where c is a positive constant, and
is a constant 
.
L-notation is used mostly in computational number theory
, to express the complexity of algorithms for difficult number theory
problems, eg. sieves for integer factorization
and methods for solving discrete logarithm
s. The benefit of this notation is that it simplifies the analysis of these algorithms. The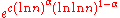
expresses the dominant term, and the 
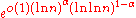takes care of everything smaller.
When
is 0, then
is a polynomial function of ln n; when
is 1 then
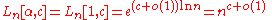
is a fully exponential function
of ln n (and thereby polynomial in n).
If
is between 0 and 1, the function is subexponential (and superpolynomial).
algorithms have subexponential time complexities. The best is the general number field sieve
, which has an expected running time of
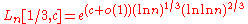
for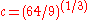
. The best such algorithm prior to the number field sieve was the quadratic sieve
which has running time
.
For the elliptic curve
discrete logarithm
problem, the fastest general purpose algorithm is the baby-step giant-step
algorithm, which has a running time on the order of the square-root of the group order n. In L-notation this would be
.
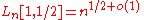The existence of the AKS primality test
, which runs in polynomial time, means that the time complexity for primality testing is known to be at most
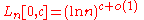
where c has been proven to be at most 6.
in his paper "Analysis and comparison of some integer factoring algorithms". This form had only the
parameter: the 
in the formula was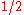 
for the algorithms he was analyzing. Pomerance had been using the letter 
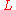(or lower case 
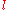) in this and previous papers for formulae that involved many logarithms.
The formula above involving two parameters was introduced by Arjen Lenstra
and Hendrik Lenstra
in their article on "Algorithms in Number Theory". It was introduced in their analysis of a Discrete logarithm
algorithm of Coppersmith
. This is the most commonly used form in the literature today.
The Handbook of Applied Cryptography defines the L-notation with a big
around the formula presented in this article. This is not the standard definition. The big 
would suggest that the running time is an upper bound. However, for the integer factoring and discrete logarithm algorithms that L-notation is commonly used for, the running time is not an upper bound, so this definition is not preferred.
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
notation analogous to big-O notation, denoted as
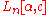for a bound variable tending to infinityLimit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
. Like big-O notation, it is usually used to roughly convey the computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
of a particular algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
.
It is defined as
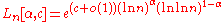,where c is a positive constant, and
is a constant .L-notation is used mostly in computational number theory
Computational number theory
In mathematics, computational number theory, also known as algorithmic number theory, is the study of algorithms for performing number theoretic computations...
, to express the complexity of algorithms for difficult number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
problems, eg. sieves for integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
and methods for solving discrete logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
s. The benefit of this notation is that it simplifies the analysis of these algorithms. The
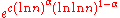expresses the dominant term, and the 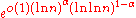takes care of everything smaller.When
is 0, thenis a polynomial function of ln n; when
is 1 then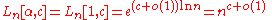is a fully exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
of ln n (and thereby polynomial in n).
If
is between 0 and 1, the function is subexponential (and superpolynomial).Examples
Many general-purpose integer factorizationInteger factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
algorithms have subexponential time complexities. The best is the general number field sieve
General number field sieve
In number theory, the general number field sieve is the most efficient classical algorithm known for factoring integers larger than 100 digits...
, which has an expected running time of
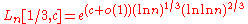
for
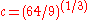. The best such algorithm prior to the number field sieve was the quadratic sieveQuadratic sieve
The quadratic sieve algorithm is a modern integer factorization algorithm and, in practice, the second fastest method known . It is still the fastest for integers under 100 decimal digits or so, and is considerably simpler than the number field sieve...
which has running time
.For the elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
discrete logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
problem, the fastest general purpose algorithm is the baby-step giant-step
Baby-step giant-step
In group theory, a branch of mathematics, the baby-step giant-step is a meet-in-the-middle algorithm computing the discrete logarithm. The discrete log problem is of fundamental importance to the area of public key cryptography...
algorithm, which has a running time on the order of the square-root of the group order n. In L-notation this would be
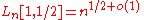.The existence of the AKS primality test
AKS primality test
The AKS primality test is a deterministic primality-proving algorithm created and published by three Indian Institute of Technology Kanpur computer scientists, Manindra Agrawal, Neeraj Kayal, and Nitin Saxena, on August 6, 2002, in a paper titled "PRIMES is in P"...
, which runs in polynomial time, means that the time complexity for primality testing is known to be at most
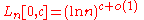
where c has been proven to be at most 6.
History
L-notation has been defined in various forms throughout the literature. The first use of it came from Carl PomeranceCarl Pomerance
Carl Bernard Pomerance is a well-known number theorist. He attended college at Brown University and later received his Ph.D. from Harvard University in 1972 with a dissertation proving that any odd perfect number has at least 7 distinct prime factors. He immediately joined the faculty at the...
in his paper "Analysis and comparison of some integer factoring algorithms". This form had only the
parameter: the in the formula was 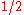for the algorithms he was analyzing. Pomerance had been using the letter 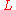(or lower case 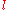) in this and previous papers for formulae that involved many logarithms.The formula above involving two parameters was introduced by Arjen Lenstra
Arjen Lenstra
Arjen Klaas Lenstra is a Dutch mathematician. He studied mathematics at the University of Amsterdam.He is currently a professor at the EPFL , in the Laboratory for Cryptologic Algorithms, and...
and Hendrik Lenstra
Hendrik Lenstra
Hendrik Willem Lenstra, Jr. is a Dutch mathematician.-Biography:Lenstra received his doctorate from the University of Amsterdam in 1977 and became a professor there in 1978...
in their article on "Algorithms in Number Theory". It was introduced in their analysis of a Discrete logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
algorithm of Coppersmith
Don Coppersmith
Don Coppersmith is a cryptographer and mathematician. He was involved in the design of the Data Encryption Standard block cipher at IBM, particularly the design of the S-boxes, strengthening them against differential cryptanalysis...
. This is the most commonly used form in the literature today.
The Handbook of Applied Cryptography defines the L-notation with a big
around the formula presented in this article. This is not the standard definition. The big would suggest that the running time is an upper bound. However, for the integer factoring and discrete logarithm algorithms that L-notation is commonly used for, the running time is not an upper bound, so this definition is not preferred.