Factor base
Encyclopedia
In computational number theory
, the factor base is a mathematical tool commonly used in algorithms involving extensive sieving
of potential factors.
of prime number
s P. Say we want to factorize an integer n. We generate, in some way, a large number of integer pairs (x, y) for which
and 
, and x, y can be completely factorized over the chosen factor base—that is, they are p-smooth
for the largest prime p in P.
We find a subset S of the integer pairs such that
and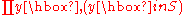 
are both perfect square
s. Over our factor base this reduces to adding exponents of their prime factors, modulo 2
, as we can distinguish squares from non-squares simply by checking the parity of the exponents.
We can represent each x and y as a vector
of a matrix
with 0 and 1 entries for the parity of each exponent. This essentially reformulates the problem into a system of linear equations, which can be solved using numerous methods such as Gaussian elimination
; in practice advanced methods like the block Lanczos algorithm
are used, that take advantage of certain properties of the system.
Once such a subset is found, we have essentially found a congruence of squares
modulo n and can attempt to factorize n. This congruence may generate the trivial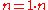
; in this case we try to find another suitable subset. If no such subset is found, we can search for more (x, y) pairs, or try again using a different factor base.
, the quadratic sieve
, and the number field sieve
. The difference between these algorithms is essentially the methods used to generate (x, y) candidates.
Computational number theory
In mathematics, computational number theory, also known as algorithmic number theory, is the study of algorithms for performing number theoretic computations...
, the factor base is a mathematical tool commonly used in algorithms involving extensive sieving
Sieve theory
Sieve theory is a set of general techniques in number theory, designed to count, or more realistically to estimate the size of, sifted sets of integers. The primordial example of a sifted set is the set of prime numbers up to some prescribed limit X. Correspondingly, the primordial example of a...
of potential factors.
Usage
The factor base is a relatively small setSet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s P. Say we want to factorize an integer n. We generate, in some way, a large number of integer pairs (x, y) for which
and , and x, y can be completely factorized over the chosen factor base—that is, they are p-smoothSmooth number
In number theory, a smooth number is an integer which factors completely into small prime numbers. The term seems to have been coined by Leonard Adleman. Smooth numbers are especially important in cryptography relying on factorization.-Definition:...
for the largest prime p in P.
We find a subset S of the integer pairs such that
and 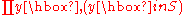are both perfect squareSquare number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
s. Over our factor base this reduces to adding exponents of their prime factors, modulo 2
GF(2)
GF is the Galois field of two elements. It is the smallest finite field.- Definition :The two elements are nearly always called 0 and 1, being the additive and multiplicative identities, respectively...
, as we can distinguish squares from non-squares simply by checking the parity of the exponents.
We can represent each x and y as a vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with 0 and 1 entries for the parity of each exponent. This essentially reformulates the problem into a system of linear equations, which can be solved using numerous methods such as Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
; in practice advanced methods like the block Lanczos algorithm
Block Lanczos algorithm for nullspace of a matrix over a finite field
The block Lanczos algorithm for nullspace of a matrix over a finite field is a procedure for finding the nullspace of a matrix using only multiplication of the matrix by long, thin matrices...
are used, that take advantage of certain properties of the system.
Once such a subset is found, we have essentially found a congruence of squares
Congruence of squares
In number theory, a congruence of squares is a congruence commonly used in integer factorization algorithms.-Derivation:Given a positive integer n, Fermat's factorization method relies on finding numbers x, y satisfying the equality...
modulo n and can attempt to factorize n. This congruence may generate the trivial
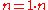; in this case we try to find another suitable subset. If no such subset is found, we can search for more (x, y) pairs, or try again using a different factor base.Algorithms
Factor bases are used in, for example, Dixon's factorizationDixon's factorization method
In number theory, Dixon's factorization method is a general-purpose integer factorization algorithm; it is the prototypical factor base method, and the only factor base method for which a run-time bound not reliant on conjectures about the smoothness properties of values of a polynomial is...
, the quadratic sieve
Quadratic sieve
The quadratic sieve algorithm is a modern integer factorization algorithm and, in practice, the second fastest method known . It is still the fastest for integers under 100 decimal digits or so, and is considerably simpler than the number field sieve...
, and the number field sieve
General number field sieve
In number theory, the general number field sieve is the most efficient classical algorithm known for factoring integers larger than 100 digits...
. The difference between these algorithms is essentially the methods used to generate (x, y) candidates.