
Quantum gate
Encyclopedia
In quantum computing and specifically the quantum circuit
model of computation, a quantum gate (or quantum logic gate) is a basic quantum circuit
operating on a small number of qubit
s. They are the building blocks of quantum circuits, like classical logic gate
s are for conventional digital circuits.
Unlike many classical logic gates, quantum logic gates are reversible
. However, classical computing can be performed using only reversible gates. For example, the reversible Toffoli gate
can implement all Boolean functions. This gate
has a direct quantum equivalent, showing that quantum circuits can perform all operations performed by classical circuits.
Quantum logic gates are represented by unitary matrices. The most common quantum gates operate on spaces of one or two qubits, just like the common classical logic gates operate on one or two bits. This means that as matrices, quantum gates can be described by 2 × 2 or 4 × 4 unitary matrices.
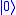 to
to 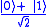 and
and  to
to 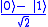 and represents a rotation of
and represents a rotation of  about the x- and z-axes. It is represented by the Hadamard matrix
about the x- and z-axes. It is represented by the Hadamard matrix
:
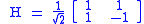 .
.
Since the rows of the matrix are orthogonal, H is indeed a unitary matrix.
around the X-axis by π radians. It maps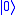 to
to 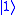 and
and 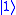 to
to  . It is represented by the Pauli
. It is represented by the Pauli
X matrix: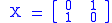 .
.
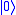 to
to 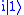 and
and 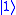 to
to 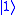 . It is represented by the Pauli
. It is represented by the Pauli
Y matrix: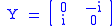 .
.
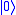 unchanged and maps
unchanged and maps 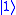 to
to 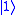 . It is represented by the Pauli
. It is represented by the Pauli
Z matrix: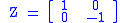 .
.
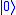 unchanged and map
unchanged and map 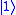 to
to 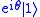 . The probability of measuring a
. The probability of measuring a 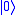 or
or 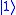 is unchanged after applying this gate, however it modifies the phase of the quantum state. This is equivalent to tracing a horizontal circle (a line of latitude) on the Bloch Sphere by
is unchanged after applying this gate, however it modifies the phase of the quantum state. This is equivalent to tracing a horizontal circle (a line of latitude) on the Bloch Sphere by 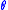 radians.
radians.
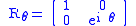
where θ is the phase shift. Some common examples are the gate where θ =
gate where θ = 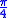 , the phase gate where θ =
, the phase gate where θ = 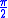 and the Pauli-Z gate where θ = π.
and the Pauli-Z gate where θ = π.
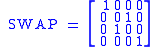 .
.
(or CNOT) acts on 2 qubits, and performs the NOT operation on the second qubit only when the first qubit is , and otherwise leaves it unchanged. It is represented by the matrix
, and otherwise leaves it unchanged. It is represented by the matrix
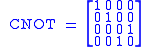 .
.
More generally if U is a gate that operates on single qubits with matrix representation ,
,
then the controlled-U gate is a gate that operates on two qubits in such a way that the first qubit serves as a control. It maps the basis states as follows.
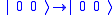

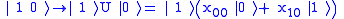
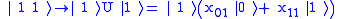
The matrix representing the controlled U is
 .
.
When U is one of the Pauli matrices
, σx, σy, or σz, the respective terms "controlled-X", "controlled-Y", or "controlled-Z" are sometimes used.
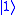 , it applies a Pauli-X on the third bit, else it does nothing. It is an example of a controlled gate. Since it is the quantum analog of a classical gate, it is completely specified by its truth table.
, it applies a Pauli-X on the third bit, else it does nothing. It is an example of a controlled gate. Since it is the quantum analog of a classical gate, it is completely specified by its truth table.
It can be also described as the gate which maps to
to  .
.
means the same number of balls are output as input. This corresponds nicely to the conservation of mass
in physics, and helps to show that the model is not wasteful.
It can be also described as the gate which maps to
to  .
.
One simple set of two-qubit universal quantum gates is the Hadamard gate ( ), the
), the 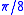 gate
gate 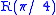 , and the controlled NOT gate.
, and the controlled NOT gate.
A single-gate set of universal quantum gates can also be formulated using the three-qubit Deutsch gate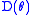 , which performs the transformation
, which performs the transformation

The universal classical logic gate, the Toffoli gate
, is reducible to the Deutsch gate,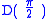 , thus showing that all classical logic operations can be performed on a universal quantum computer.
, thus showing that all classical logic operations can be performed on a universal quantum computer.
Quantum circuit
In quantum information theory, a quantum circuit is a model for quantum computation in which a computation is a sequence of quantum gates, which are reversible transformations on a quantum mechanical analog of an n-bit register...
model of computation, a quantum gate (or quantum logic gate) is a basic quantum circuit
Quantum circuit
In quantum information theory, a quantum circuit is a model for quantum computation in which a computation is a sequence of quantum gates, which are reversible transformations on a quantum mechanical analog of an n-bit register...
operating on a small number of qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s. They are the building blocks of quantum circuits, like classical logic gate
Logic gate
A logic gate is an idealized or physical device implementing a Boolean function, that is, it performs a logical operation on one or more logic inputs and produces a single logic output. Depending on the context, the term may refer to an ideal logic gate, one that has for instance zero rise time and...
s are for conventional digital circuits.
Unlike many classical logic gates, quantum logic gates are reversible
Reversible computing
Reversible computing is a model of computing where the computational process to some extent is reversible, i.e., time-invertible. A necessary condition for reversibility of a computational model is that the transition function mapping states to their successors at a given later time should be...
. However, classical computing can be performed using only reversible gates. For example, the reversible Toffoli gate
Toffoli gate
In computer science, the Toffoli gate , invented by Tommaso Toffoli, is a universal reversible logic gate, which means that any reversible circuit can be constructed from Toffoli gates...
can implement all Boolean functions. This gate
has a direct quantum equivalent, showing that quantum circuits can perform all operations performed by classical circuits.
Quantum logic gates are represented by unitary matrices. The most common quantum gates operate on spaces of one or two qubits, just like the common classical logic gates operate on one or two bits. This means that as matrices, quantum gates can be described by 2 × 2 or 4 × 4 unitary matrices.
Commonly used gates
Quantum gates are usually represented as matrices. A gate which acts on k qubits is represented by a 2k x 2k unitary matrix. The number of qubits in the input and output of the gate have to be equal. The action of the quantum gate is found by multiplying the matrix representing the gate with the vector which represents the quantum state.Hadamard gate
The Hadamard gate acts on a single qubit. It maps the basis state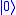 to
to 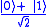 and
and  to
to 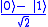 and represents a rotation of
and represents a rotation of  about the x- and z-axes. It is represented by the Hadamard matrix
about the x- and z-axes. It is represented by the Hadamard matrixHadamard matrix
In mathematics, an Hadamard matrix, named after the French mathematician Jacques Hadamard, is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal...
:
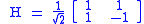 .
.Since the rows of the matrix are orthogonal, H is indeed a unitary matrix.
Pauli-X gate
The Pauli-X gate acts on a single qubit. It is the quantum equivalent of a NOT gate. It equates to a rotation of the Bloch SphereBloch sphere
In quantum mechanics, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system , named after the physicist Felix Bloch....
around the X-axis by π radians. It maps
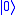 to
to 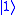 and
and 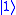 to
to  . It is represented by the Pauli
. It is represented by the PauliPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
X matrix:
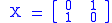 .
.Pauli-Y gate
The Pauli-Y gate acts on a single qubit. It equates to a rotation around the Y-axis of the Bloch Sphere by π radians. It maps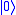 to
to 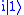 and
and 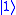 to
to 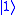 . It is represented by the Pauli
. It is represented by the PauliPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
Y matrix:
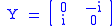 .
.Pauli-Z gate
The Pauli-Z gate acts on a single qubit. It equates to a rotation around the Z-axis of the Bloch Sphere by π radians. Thus, it is a special case of a phase shift gate with θ=π. It leaves the basis state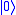 unchanged and maps
unchanged and maps 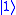 to
to 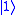 . It is represented by the Pauli
. It is represented by the PauliPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
Z matrix:
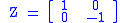 .
.Phase shift gates
This is a family of single-qubit gates that leave the basis state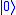 unchanged and map
unchanged and map 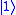 to
to 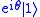 . The probability of measuring a
. The probability of measuring a 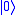 or
or 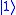 is unchanged after applying this gate, however it modifies the phase of the quantum state. This is equivalent to tracing a horizontal circle (a line of latitude) on the Bloch Sphere by
is unchanged after applying this gate, however it modifies the phase of the quantum state. This is equivalent to tracing a horizontal circle (a line of latitude) on the Bloch Sphere by 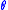 radians.
radians.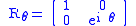
where θ is the phase shift. Some common examples are the
 gate where θ =
gate where θ = 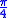 , the phase gate where θ =
, the phase gate where θ = 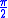 and the Pauli-Z gate where θ = π.
and the Pauli-Z gate where θ = π.Swap gate
The swap gate swaps two qubits. It is represented by the matrix: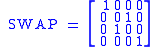 .
.Controlled gates
Controlled gates act on 2 or more qubits, where one or more qubits act as a control for some operation. For example, the controlled NOT gateControlled NOT gate
The Controlled NOT gate is a quantum gate that is an essential component in the construction of a quantum computer. It can be used to disentangle EPR states...
(or CNOT) acts on 2 qubits, and performs the NOT operation on the second qubit only when the first qubit is
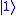 , and otherwise leaves it unchanged. It is represented by the matrix
, and otherwise leaves it unchanged. It is represented by the matrix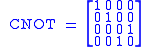 .
.More generally if U is a gate that operates on single qubits with matrix representation
 ,
,then the controlled-U gate is a gate that operates on two qubits in such a way that the first qubit serves as a control. It maps the basis states as follows.
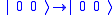

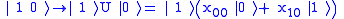
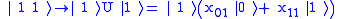
The matrix representing the controlled U is
 .
.When U is one of the Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
, σx, σy, or σz, the respective terms "controlled-X", "controlled-Y", or "controlled-Z" are sometimes used.
Toffoli gate
The Toffoli gate, also CCNOT gate, is a 3-bit gate, which is universal for classical computation. The quantum Toffoli gate is the same gate, defined for 3 qubits. If the first two bits are in the state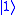 , it applies a Pauli-X on the third bit, else it does nothing. It is an example of a controlled gate. Since it is the quantum analog of a classical gate, it is completely specified by its truth table.
, it applies a Pauli-X on the third bit, else it does nothing. It is an example of a controlled gate. Since it is the quantum analog of a classical gate, it is completely specified by its truth table.
| INPUT | OUTPUT | ||||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 |
It can be also described as the gate which maps
 to
to  .
.Fredkin gate
The Fredkin gate (also CSWAP gate) is a 3-bit gate that performs a controlled swap. It is universal for classical computation. It has the useful property that the numbers of 0s and 1s are conserved throughout, which in the billiard ball modelBilliard-Ball Computer
A billiard ball computer, also known as a conservative logic circuit, is an idealized model of a reversible mechanical computer based on newtonian dynamics, proposed in 1982 by Edward Fredkin and Tommaso Toffoli...
means the same number of balls are output as input. This corresponds nicely to the conservation of mass
Conservation of mass
The law of conservation of mass, also known as the principle of mass/matter conservation, states that the mass of an isolated system will remain constant over time...
in physics, and helps to show that the model is not wasteful.
| INPUT | OUTPUT | ||||
|---|---|---|---|---|---|
| C | I1 | I2 | C | O1 | O2 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
It can be also described as the gate which maps
 to
to  .
.Universal quantum gates
Informally, a set of universal quantum gates is any set of gates to which any operation possible on a quantum computer can be reduced, that is, any other unitary operation can be expressed as a finite sequence of gates from the set. Technically, this is impossible since the number of possible quantum gates is uncountable, whereas the number of finite sequences from a finite set is countable. To solve this problem, we only require that any quantum operation can be approximated by a sequence of gates from this finite set. Moreover, for the specific case of single qubit unitaries the Solovay–Kitaev theorem guarantees that this can be done efficiently.One simple set of two-qubit universal quantum gates is the Hadamard gate (
 ), the
), the 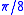 gate
gate 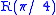 , and the controlled NOT gate.
, and the controlled NOT gate.A single-gate set of universal quantum gates can also be formulated using the three-qubit Deutsch gate
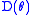 , which performs the transformation
, which performs the transformation
The universal classical logic gate, the Toffoli gate
Toffoli gate
In computer science, the Toffoli gate , invented by Tommaso Toffoli, is a universal reversible logic gate, which means that any reversible circuit can be constructed from Toffoli gates...
, is reducible to the Deutsch gate,
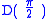 , thus showing that all classical logic operations can be performed on a universal quantum computer.
, thus showing that all classical logic operations can be performed on a universal quantum computer.
