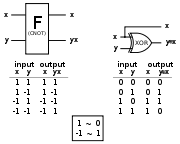
The Controlled NOT gate (also C-NOT or CNOT) is a quantum gate

Quantum gate

In quantum computing and specifically the quantum circuit model of computation, a quantum gate is a basic quantum circuit operating on a small number of qubits. They are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.Unlike many classical...

 that is an essential component in the construction of a quantum computer

Quantum computer

A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...

. It can be used to disentangle EPR states. Specifically, any quantum circuit can be simulated to an arbitrary degree of accuracy using a combination of CNOT gates and single qubit

Qubit

In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....

 rotations.

Operation

The CNOT gate flips the second qubit (the target qubit) if and only if the first qubit (the control qubit) is 1.

Before		After
Control	Target	Control	Target
0	0	0	0
0	1	0	1
1	0	1	1
1	1	1	0

The resulting value of the second qubit corresponds to the result of a classical XOR gate

XOR gate

The XOR gate is a digital logic gate that implements an exclusive or; that is, a true output results if one, and only one, of the inputs to the gate is true . If both inputs are false or both are true , a false output results. Its behavior is summarized in the truth table shown on the right...

.

The CNOT gate can be represented by the matrix:


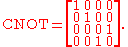
The first experimental realization of a CNOT gate was accomplished in 1995. Here, a single Beryllium ion in a trap was used. The two qubits were encoded into an optical state and into the vibrational state of the ion within the trap. At the time of the experiment, the reliability of the CNOT-operation was measured to be on the order of 90%.

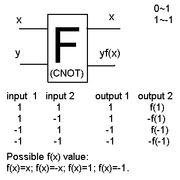
In addition to a regular Controlled NOT gate, one could construct a Function-Controlled NOT gate, which accepts an arbitrary number n+1 of qubits as input, where n+1 is greater than or equal to 2 (a quantum register

Quantum register

A quantum register is the quantum mechanical analogue of a classical processor register.A mathematical description of a quantum register is achieved by using a tensor product of qubit bra or ket vectors...

). This gate flips the last qubit of the register if and only if a built-in function, with the first n qubits as input, returns a 1.
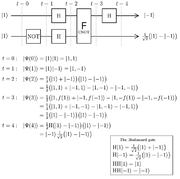
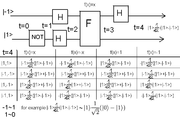
The Function-Controlled NOT gate is an essential element of the Deutsch-Jozsa algorithm

Deutsch-Jozsa algorithm

The Deutsch–Jozsa algorithm is a quantum algorithm, proposed by David Deutsch and Richard Jozsa in 1992 with improvements by Richard Cleve, Artur Ekert, Chiara Macchiavello, and Michele Mosca in 1998...

.
CNOT is also a kind of universal gate(in the classical sense of the word). It is easy to see that if the CONTROL is set to '1' the TARGET output is always NOT. So, a NOT GATE can be constructed using CNOT. Further, we can construct an AND GATE by using two CNOTs. Look at the table below

Before		After
Control	Target	Control	Target
0	0	0	0
0	1	0	1
1	0	1	1
1	1	1	0

Before		After
Control	Target	Control	Target
0	0	0	0
1	0	0	0
1	1	1	0
0	1	1	1

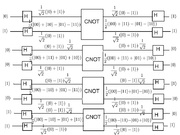
Proof of operation

Let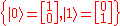 be the orthonormal basis

Orthonormal basis

In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...

 (using Bra-ket notation

Bra-ket notation

Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...

).

Let .

Let be the flip qubit of .

Recall that .

When control qubit is 0

First, we shall prove that :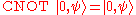

Before we compute, however, note that our specific definition of assumes an eigenbasis of



Then, it's not difficult to verify that


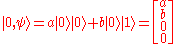
Then

Matrix multiplication

In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...

.

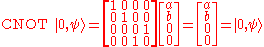Therefore CNOT doesn't change the 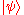qubit if the first qubit is 0.

When control qubit is 1

Now, we shall prove that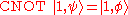 , which means that the CNOT gate flips the 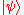qubit.

Similarly to the first demonstration, we have .

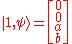Then

As we can see that

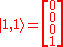
and
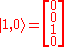, using these on the equation above gives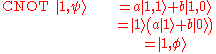



Therefore the CNOT gate flips the 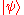qubit into if the control qubit is set to 1. A simple way to observe this is to multiply the CNOT matrix by a column vector, noticing that the operation on the first bit is identity, and a NOT gate on the second bit.