Deutsch-Jozsa algorithm
Encyclopedia
The Deutsch–Jozsa algorithm is a quantum algorithm
, proposed by David Deutsch
and Richard Jozsa
in 1992 with improvements by Richard Cleve
, Artur Ekert
, Chiara Macchiavello, and Michele Mosca
in 1998. Although it is of little practical use, it is one of the first examples of a quantum algorithm that is exponentially faster than any possible deterministic classical algorithm.
that implements the function . We are promised
. We are promised
that the function is either constant
(0 on all inputs or 1 on all inputs) or balanced (returns 1 for half of the input domain and 0 for the other half); the task then is to determine if is constant or balanced by using the oracle.
is constant or balanced by using the oracle.
oracle
s relative to which P
and NP
are separated. In analogy, we can have oracles relative to which EQP
and P are separated. This tells us nothing about BPP or BQP
, though.
For the Deutsch-Jozsa oracle, P and BPP are also separated. This is because in the worst-case scenario, which can be extremely unlikely, deterministic pseudorandom queries can be anticipated and conspired against. Please note the seed can't be chosen randomly.
Simon's algorithm
is with respect to an oracle separating BQP from BPP.
 evaluations of
evaluations of  will be required in the worst case. To prove that
will be required in the worst case. To prove that  is constant, just over half the set of outputs must be evaluated and found to be identical (remembering that the function is guaranteed to be either balanced or constant, not somewhere in between). The best case occurs where the function is balanced and the first two output values that happen to be selected are different. For a conventional randomized algorithm
is constant, just over half the set of outputs must be evaluated and found to be identical (remembering that the function is guaranteed to be either balanced or constant, not somewhere in between). The best case occurs where the function is balanced and the first two output values that happen to be selected are different. For a conventional randomized algorithm
, a constant evaluations of the function suffices to produce the correct answer with a high probability (failing with probability
evaluations of the function suffices to produce the correct answer with a high probability (failing with probability  ). However,
). However,  evaluations are still required if we want an answer that is always correct. The Deutsch-Jozsa quantum algorithm produces an answer that is always correct with a single evaluation of
evaluations are still required if we want an answer that is always correct. The Deutsch-Jozsa quantum algorithm produces an answer that is always correct with a single evaluation of  .
.
Specifically we were given a boolean function whose input is 1 bit, and asked if it is constant.
and asked if it is constant.
The algorithm as Deutsch had originally proposed it was not, in fact, deterministic. The algorithm was successful with a probability of one half.
In 1992, Deutsch and Jozsa produced a deterministic algorithm which was generalized to a function which takes bits for its input. Unlike Deutsch's Algorithm, this algorithm required two function evaluations instead of only one.
bits for its input. Unlike Deutsch's Algorithm, this algorithm required two function evaluations instead of only one.
Further improvements to the Deutsch–Jozsa algorithm were made by Cleve et al., resulting in an algorithm that is both deterministic and requires only a single query of . This algorithm is still referred to as Deutsch–Jozsa algorithm in honour of the groundbreaking techniques they employed.
. This algorithm is still referred to as Deutsch–Jozsa algorithm in honour of the groundbreaking techniques they employed.
The Deutsch–Jozsa algorithm provided inspiration for Shor's algorithm
and Grover's algorithm
, two of the most revolutionary quantum algorithms.
 . It is equivalent to check
. It is equivalent to check  (where
(where  is addition modulo 2), if zero, then
is addition modulo 2), if zero, then  is constant, otherwise
is constant, otherwise  is not constant.
is not constant.
We begin with the two-qubit state and apply a Hadamard transform
and apply a Hadamard transform
to each qubit. This yields
We are given a quantum implementation of the function which maps
which maps  to
to  . Applying this function to our current state we obtain
. Applying this function to our current state we obtain


We ignore the last bit and the global phase and therefore have the state
Applying a Hadamard transform to this state we have

Obviously if and only if we measure a zero. Therefore the function is constant if and only if we measure a zero.
if and only if we measure a zero. Therefore the function is constant if and only if we measure a zero.
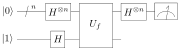 The algorithm begins with the n+1 bit state
The algorithm begins with the n+1 bit state  . That is, the first n bits are each in the state
. That is, the first n bits are each in the state  and the final bit is
and the final bit is  . A Hadamard transformation is applied to each bit to obtain the state
. A Hadamard transformation is applied to each bit to obtain the state
 .
.
We have the function implemented as quantum oracle. The oracle maps the state
implemented as quantum oracle. The oracle maps the state  to
to  . Applying the quantum oracle gives
. Applying the quantum oracle gives
 .
.
For each ,
,  is either
is either  or
or  . A quick check of these two possibilities yields
. A quick check of these two possibilities yields
 .
.
At this point the last qubit may be ignored. We apply a Hadamard transformation to each qubit to obtain

where is the sum of the bitwise product.
is the sum of the bitwise product.
Finally we examine the probability of measuring ,
,

which evaluates to 1 if is constant (constructive interference) and 0 if
is constant (constructive interference) and 0 if  is balanced (destructive interference).
is balanced (destructive interference).
Quantum algorithm
In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a...
, proposed by David Deutsch
David Deutsch
David Elieser Deutsch, FRS is an Israeli-British physicist at the University of Oxford. He is a non-stipendiary Visiting Professor in the Department of Atomic and Laser Physics at the Centre for Quantum Computation in the Clarendon Laboratory of the University of Oxford...
and Richard Jozsa
Richard Jozsa
Richard Jozsa is the holder of the Leigh Trapnell Chair in Quantum Physics at the University of Cambridge. His research area is quantum information science; a pioneer of this field, he is the co-author of the Deutsch-Jozsa quantum algorithm and one of the co-inventors of quantum teleportation...
in 1992 with improvements by Richard Cleve
Richard Cleve
Richard Erwin Cleve is a professor of computer science at the David R. Cheriton School of Computer Science at the University of Waterloo, where he holds the Institute for Quantum Computing Chair in quantum computing, and an associate member of the Perimeter Institute for Theoretical...
, Artur Ekert
Artur Ekert
Artur Ekert is a Professor of Quantum Physics at the Mathematical Institute, University of Oxford, and a Lee Kong Chian Centennial Professor at the National University of Singapore and also the Director of CQT...
, Chiara Macchiavello, and Michele Mosca
Michele Mosca
Michele Mosca is co-founder and deputy director of the Institute for Quantum Computing at the University of Waterloo, researcher and founding member of the Perimeter Institute for Theoretical Physics, and professor of mathematics in the department of at the University of Waterloo...
in 1998. Although it is of little practical use, it is one of the first examples of a quantum algorithm that is exponentially faster than any possible deterministic classical algorithm.
Problem statement
In the Deutsch-Jozsa problem, we are given a black box quantum computer known as an oracleOracle machine
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any...
that implements the function
 . We are promised
. We are promisedPromise problem
In computational complexity theory, a promise problem is a generalization of a decision problem where the input is promised to belong to a subset of all possible inputs. Unlike decision problems, the yes instances and no instances do not exhaust the set of all inputs...
that the function is either constant
Constant function
In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
(0 on all inputs or 1 on all inputs) or balanced (returns 1 for half of the input domain and 0 for the other half); the task then is to determine if
 is constant or balanced by using the oracle.
is constant or balanced by using the oracle.Motivation
It has been shown there are random string queryRandom oracle
In cryptography, a random oracle is an oracle that responds to every query with a random response chosen uniformly from its output domain, except that for any specific query, it responds the same way every time it receives that query...
oracle
Oracle
In Classical Antiquity, an oracle was a person or agency considered to be a source of wise counsel or prophetic predictions or precognition of the future, inspired by the gods. As such it is a form of divination....
s relative to which P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
and NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
are separated. In analogy, we can have oracles relative to which EQP
EQP (complexity)
In computational complexity theory, EQP , which stands for exact quantum polynomial time, is the class of decision problems solvable by a quantum computer which outputs the correct answer with probability 1 and runs in polynomial time with probability 1...
and P are separated. This tells us nothing about BPP or BQP
BQP
In computational complexity theory BQP is the class of decision problems solvable by a quantum computer in polynomial time, with an error probability of at most 1/3 for all instances...
, though.
For the Deutsch-Jozsa oracle, P and BPP are also separated. This is because in the worst-case scenario, which can be extremely unlikely, deterministic pseudorandom queries can be anticipated and conspired against. Please note the seed can't be chosen randomly.
Simon's algorithm
Simon's algorithm
Simon's algorithm, conceived by Daniel Simon in 1994, is a quantum algorithm which solves a black-box problem exponentially faster than any classical algorithm, including probabilistic algorithms...
is with respect to an oracle separating BQP from BPP.
Classical solution
For a conventional deterministic algorithm where n is number of bits/qubits, evaluations of
evaluations of  will be required in the worst case. To prove that
will be required in the worst case. To prove that  is constant, just over half the set of outputs must be evaluated and found to be identical (remembering that the function is guaranteed to be either balanced or constant, not somewhere in between). The best case occurs where the function is balanced and the first two output values that happen to be selected are different. For a conventional randomized algorithm
is constant, just over half the set of outputs must be evaluated and found to be identical (remembering that the function is guaranteed to be either balanced or constant, not somewhere in between). The best case occurs where the function is balanced and the first two output values that happen to be selected are different. For a conventional randomized algorithmRandomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
, a constant
 evaluations of the function suffices to produce the correct answer with a high probability (failing with probability
evaluations of the function suffices to produce the correct answer with a high probability (failing with probability  ). However,
). However,  evaluations are still required if we want an answer that is always correct. The Deutsch-Jozsa quantum algorithm produces an answer that is always correct with a single evaluation of
evaluations are still required if we want an answer that is always correct. The Deutsch-Jozsa quantum algorithm produces an answer that is always correct with a single evaluation of  .
.History
The Deutsch–Jozsa Algorithm generalizes earlier (1985) work by David Deutsch, which provided a solution for the simple case.Specifically we were given a boolean function whose input is 1 bit,
 and asked if it is constant.
and asked if it is constant.The algorithm as Deutsch had originally proposed it was not, in fact, deterministic. The algorithm was successful with a probability of one half.
In 1992, Deutsch and Jozsa produced a deterministic algorithm which was generalized to a function which takes
 bits for its input. Unlike Deutsch's Algorithm, this algorithm required two function evaluations instead of only one.
bits for its input. Unlike Deutsch's Algorithm, this algorithm required two function evaluations instead of only one.Further improvements to the Deutsch–Jozsa algorithm were made by Cleve et al., resulting in an algorithm that is both deterministic and requires only a single query of
 . This algorithm is still referred to as Deutsch–Jozsa algorithm in honour of the groundbreaking techniques they employed.
. This algorithm is still referred to as Deutsch–Jozsa algorithm in honour of the groundbreaking techniques they employed.The Deutsch–Jozsa algorithm provided inspiration for Shor's algorithm
Shor's algorithm
Shor's algorithm, named after mathematician Peter Shor, is a quantum algorithm for integer factorization formulated in 1994...
and Grover's algorithm
Grover's algorithm
Grover's algorithm is a quantum algorithm for searching an unsorted database with N entries in O time and using O storage space . It was invented by Lov Grover in 1996....
, two of the most revolutionary quantum algorithms.
Decoherence
For the Deutsch–Jozsa algorithm to work, the oracle computing f(x) from x has to be a quantum oracle which doesn't decohere x. It also mustn't leave any copy of x lying around at the end of the oracle call.Deutsch's Algorithm
Deutsch's algorithm is a special case of the general Deutsch–Jozsa algorithm. We need to check the condition . It is equivalent to check
. It is equivalent to check  (where
(where  is addition modulo 2), if zero, then
is addition modulo 2), if zero, then  is constant, otherwise
is constant, otherwise  is not constant.
is not constant.We begin with the two-qubit state
 and apply a Hadamard transform
and apply a Hadamard transformHadamard transform
The Hadamard transform is an example of a generalized class of Fourier transforms...
to each qubit. This yields

We are given a quantum implementation of the function
 which maps
which maps  to
to  . Applying this function to our current state we obtain
. Applying this function to our current state we obtain


We ignore the last bit and the global phase and therefore have the state

Applying a Hadamard transform to this state we have


Obviously
 if and only if we measure a zero. Therefore the function is constant if and only if we measure a zero.
if and only if we measure a zero. Therefore the function is constant if and only if we measure a zero.Deutsch–Jozsa algorithm

 . That is, the first n bits are each in the state
. That is, the first n bits are each in the state  and the final bit is
and the final bit is  . A Hadamard transformation is applied to each bit to obtain the state
. A Hadamard transformation is applied to each bit to obtain the state .
.We have the function
 implemented as quantum oracle. The oracle maps the state
implemented as quantum oracle. The oracle maps the state  to
to  . Applying the quantum oracle gives
. Applying the quantum oracle gives .
.For each
 ,
,  is either
is either  or
or  . A quick check of these two possibilities yields
. A quick check of these two possibilities yields .
.At this point the last qubit may be ignored. We apply a Hadamard transformation to each qubit to obtain

where
 is the sum of the bitwise product.
is the sum of the bitwise product.Finally we examine the probability of measuring
 ,
,
which evaluates to 1 if
 is constant (constructive interference) and 0 if
is constant (constructive interference) and 0 if  is balanced (destructive interference).
is balanced (destructive interference).
