Promise problem
Encyclopedia
In computational complexity theory
, a promise problem is a generalization of a decision problem
where the input is promised to belong to a subset of all possible inputs. Unlike decision problems, the yes instances (the inputs for which an algorithm must return yes) and no instances do not exhaust the set of all inputs. Intuitively, the algorithm has been promised that the input does indeed belong to set of yes instances or no instances. There may be inputs which are neither yes or no. If such an input is given to an algorithm for solving a promise problem, the algorithm is allowed to output anything.
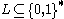, where the problem is to accept all inputs in 
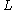and reject all inputs not in 
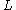. For a promise problem, there are two languages, 
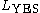and 
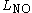, which must be disjoint, which means 
, such that all the inputs in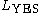 
are to be accepted and all inputs in 
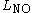are to be rejected. The set 
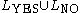is called the promise. There are no requirements on the output if the input does not belong to the promise. If the promise equals 
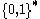, then this is also a decision problem, and the promise is said to be trivial.
, determine if the graph has a path
of length 10. The yes instances are directed acyclic graphs with a path of length 10, whereas the no instances are directed acyclic graphs with no path of length 10. The promise is the set of directed acyclic graphs. In this example, the promise is easy to check. In particular, it is very easy to check if a given graph is cyclic. However, the promised property could be difficult to evaluate. For instance, consider the problem "Given a Hamiltonian graph, determine if the graph has a cycle
of size 4." Now the promise is NP-hard
to evaluate, yet the promise problem is easy to solve since checking for cycles of size 4 can be done in polynomial time.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, a promise problem is a generalization of a decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
where the input is promised to belong to a subset of all possible inputs. Unlike decision problems, the yes instances (the inputs for which an algorithm must return yes) and no instances do not exhaust the set of all inputs. Intuitively, the algorithm has been promised that the input does indeed belong to set of yes instances or no instances. There may be inputs which are neither yes or no. If such an input is given to an algorithm for solving a promise problem, the algorithm is allowed to output anything.
Formal definition
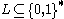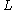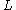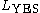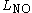A decision problem can be associated with a language, where the problem is to accept all inputs in and reject all inputs not in . For a promise problem, there are two languages, and , which must be disjoint, which means , such that all the inputs in 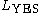are to be accepted and all inputs in 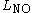are to be rejected. The set 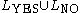is called the promise. There are no requirements on the output if the input does not belong to the promise. If the promise equals 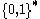, then this is also a decision problem, and the promise is said to be trivial.Examples
Many natural problems are actually promise problems. For instance, consider the following problem: Given a directed acyclic graphDirected acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
, determine if the graph has a path
Path (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
of length 10. The yes instances are directed acyclic graphs with a path of length 10, whereas the no instances are directed acyclic graphs with no path of length 10. The promise is the set of directed acyclic graphs. In this example, the promise is easy to check. In particular, it is very easy to check if a given graph is cyclic. However, the promised property could be difficult to evaluate. For instance, consider the problem "Given a Hamiltonian graph, determine if the graph has a cycle
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
of size 4." Now the promise is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
to evaluate, yet the promise problem is easy to solve since checking for cycles of size 4 can be done in polynomial time.
See also
- Computational problemComputational problemIn theoretical computer science, a computational problem is a mathematical object representing a collection of questions that computers might want to solve. For example, the problem of factoring...
- Decision problemDecision problemIn computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
- Optimization problemOptimization problemIn mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
- Search problemSearch problemIn computational complexity theory and computability theory, a search problem is a type of computational problem represented by a binary relation...
- Counting problem (complexity)
- Function problemFunction problemIn computational complexity theory, a function problem is a computational problem where a single output is expected for every input, but the output is more complex than that of a decision problem, that is, it isn't just YES or NO...