
Quantum Fourier transform
Encyclopedia
In quantum computing, the quantum Fourier transform is a linear transformation
on quantum bits
, and is the quantum analogue of the discrete Fourier transform
. The quantum Fourier transform is a part of many quantum algorithms, notably Shor's algorithm
for factoring and computing the discrete logarithm
, the quantum phase estimation algorithm
for estimating the eigenvalues of a unitary operator
, and algorithms for the hidden subgroup problem
.
The quantum Fourier transform can be performed efficiently on a quantum computer, with a particular decomposition into a product of simpler unitary matrices. Using a simple decomposition, the discrete Fourier transform can be implemented as a quantum circuit
consisting of only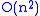 Hadamard gates and controlled phase shift gates, where
Hadamard gates and controlled phase shift gates, where  is the number of qubits. This can be compared with the classical discrete Fourier transform, which takes
is the number of qubits. This can be compared with the classical discrete Fourier transform, which takes 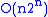 gates (where
gates (where  is the number of bits), which is exponentially more than
is the number of bits), which is exponentially more than 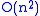 . However, the quantum Fourier transform acts on a quantum state, whereas the classical Fourier transform acts on a vector, so the quantum Fourier transform can not give a generic exponential speedup for any task which requires the classical Fourier transform.
. However, the quantum Fourier transform acts on a quantum state, whereas the classical Fourier transform acts on a vector, so the quantum Fourier transform can not give a generic exponential speedup for any task which requires the classical Fourier transform.
The best quantum Fourier transform algorithms known today require only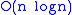 gates to achieve an efficient approximation.
gates to achieve an efficient approximation.
in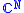 , (x0, ..., xN−1) and maps it to the vector (y0, ..., yN−1) according to the formula:
, (x0, ..., xN−1) and maps it to the vector (y0, ..., yN−1) according to the formula:

where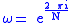 is a primitive Nth root of unity
is a primitive Nth root of unity
.
Similarly, the quantum Fourier transform acts on a quantum state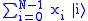 and maps it to a quantum state
and maps it to a quantum state 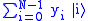 according to the formula:
according to the formula:
 .
.
This can also be expressed as the map
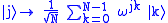 .
.
Equivalently, the quantum Fourier transform can be viewed as a unitary matrix acting on quantum state vectors, where the unitary matrix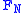 is given by
is given by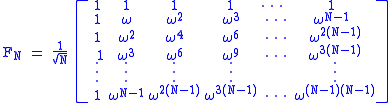 .
.
. This can be checked by performing matrix multiplication
and ensuring that the relation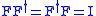 holds. Alternately, one can check that vectors of norm
holds. Alternately, one can check that vectors of norm
1 get mapped to vectors of norm 1.
From the unitary property it follows that the inverse of the quantum Fourier transform is the Hermitian adjoint of the Fourier matrix, thus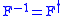 . Since there is an efficient quantum circuit implementing the quantum Fourier transform, the circuit can be run in reverse to perform the inverse quantum Fourier transform. Thus both transforms can be efficiently performed on a quantum computer.
. Since there is an efficient quantum circuit implementing the quantum Fourier transform, the circuit can be run in reverse to perform the inverse quantum Fourier transform. Thus both transforms can be efficiently performed on a quantum computer.
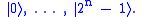
Each basis state index can be represented in binary form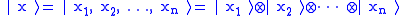
where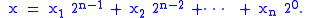
Similarly, we also adopt the notation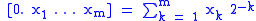 .
.
For instance,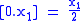 and
and 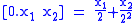 .
.
With this notation, the action of the quantum Fourier transform can be expressed as: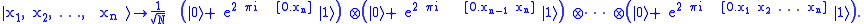
In other words, the discrete Fourier transform, an operation on n-qubits, can be factored into the tensor product of n single-qubit operations, suggesting it is easily represented as a quantum circuit
. In fact, each of those single-qubit operations can be implemented efficiently using a Hadamard gate and controlled phase gates. The first term requires one Hadamard gate, the next one requires a Hadamard gate and a controlled phase gate, and each following term requires an additional controlled phase gate. Summing up the number of gates gives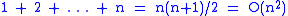 gates, which is polynomial in the number of qubits.
gates, which is polynomial in the number of qubits.
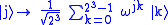 ,
,
where is a primitive eighth root of unity
is a primitive eighth root of unity
satisfying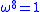 (since
(since 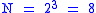 ).
).
The matrix representing this transformation on 3 qubits is
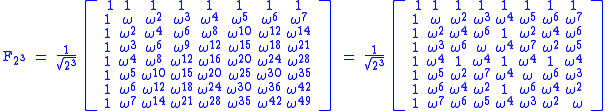 .
.
The 3-qubit quantum Fourier transform is the following operation: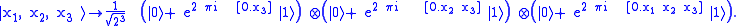
This quantum circuit implements the quantum Fourier transform on the quantum state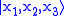 .
.
The quantum gate
s used in the circuit above are the Hadamard gate and the controlled phase gate .
.
As calculated above, the number of gates used is which is equal to 6, for n = 3.
which is equal to 6, for n = 3.
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
on quantum bits
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
, and is the quantum analogue of the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
. The quantum Fourier transform is a part of many quantum algorithms, notably Shor's algorithm
Shor's algorithm
Shor's algorithm, named after mathematician Peter Shor, is a quantum algorithm for integer factorization formulated in 1994...
for factoring and computing the discrete logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
, the quantum phase estimation algorithm
Quantum phase estimation algorithm
In quantum computing, the quantum phase estimation algorithm is a quantum algorithm that finds many applications as a subroutine in other algorithms...
for estimating the eigenvalues of a unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
, and algorithms for the hidden subgroup problem
Hidden subgroup problem
The hidden subgroup problem is a topic of research in mathematics and theoretical computer science.-Problem statement:Given a group G, a subgroup H ≤ G, and a set X, we say a function f : G → X hides the subgroup H if for all g1, g2 ∈ G,f = f if and only if g1H = g2H for the cosets of...
.
The quantum Fourier transform can be performed efficiently on a quantum computer, with a particular decomposition into a product of simpler unitary matrices. Using a simple decomposition, the discrete Fourier transform can be implemented as a quantum circuit
Quantum circuit
In quantum information theory, a quantum circuit is a model for quantum computation in which a computation is a sequence of quantum gates, which are reversible transformations on a quantum mechanical analog of an n-bit register...
consisting of only
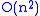 Hadamard gates and controlled phase shift gates, where
Hadamard gates and controlled phase shift gates, where  is the number of qubits. This can be compared with the classical discrete Fourier transform, which takes
is the number of qubits. This can be compared with the classical discrete Fourier transform, which takes 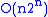 gates (where
gates (where  is the number of bits), which is exponentially more than
is the number of bits), which is exponentially more than 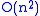 . However, the quantum Fourier transform acts on a quantum state, whereas the classical Fourier transform acts on a vector, so the quantum Fourier transform can not give a generic exponential speedup for any task which requires the classical Fourier transform.
. However, the quantum Fourier transform acts on a quantum state, whereas the classical Fourier transform acts on a vector, so the quantum Fourier transform can not give a generic exponential speedup for any task which requires the classical Fourier transform.The best quantum Fourier transform algorithms known today require only
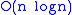 gates to achieve an efficient approximation.
gates to achieve an efficient approximation.Definition
The quantum Fourier transform is the classical discrete Fourier transform applied to the vector of amplitudes of a quantum state. The classical (unitary) Fourier transform acts on a vectorVector (mathematics and physics)
In mathematics and physics, a vector is an element of a vector space. If n is a non negative integer and K is either the field of the real numbers or the field of the complex number, then K^n is naturally endowed with a structure of vector space, where K^n is the set of the ordered sequences of n...
in
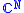 , (x0, ..., xN−1) and maps it to the vector (y0, ..., yN−1) according to the formula:
, (x0, ..., xN−1) and maps it to the vector (y0, ..., yN−1) according to the formula:
where
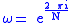 is a primitive Nth root of unity
is a primitive Nth root of unityRoot of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
.
Similarly, the quantum Fourier transform acts on a quantum state
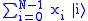 and maps it to a quantum state
and maps it to a quantum state 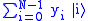 according to the formula:
according to the formula: .
.This can also be expressed as the map
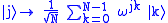 .
.Equivalently, the quantum Fourier transform can be viewed as a unitary matrix acting on quantum state vectors, where the unitary matrix
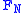 is given by
is given by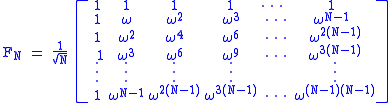 .
.Unitarity
Most of the properties of the quantum Fourier transform follow from the fact that it is a unitary transformationUnitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
. This can be checked by performing matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
and ensuring that the relation
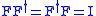 holds. Alternately, one can check that vectors of norm
holds. Alternately, one can check that vectors of normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
1 get mapped to vectors of norm 1.
From the unitary property it follows that the inverse of the quantum Fourier transform is the Hermitian adjoint of the Fourier matrix, thus
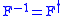 . Since there is an efficient quantum circuit implementing the quantum Fourier transform, the circuit can be run in reverse to perform the inverse quantum Fourier transform. Thus both transforms can be efficiently performed on a quantum computer.
. Since there is an efficient quantum circuit implementing the quantum Fourier transform, the circuit can be run in reverse to perform the inverse quantum Fourier transform. Thus both transforms can be efficiently performed on a quantum computer.Circuit implementation
The quantum Fourier transform can be approximately implemented for any N, however, the implementation for the case where N is a power of 2 is much simpler. Suppose N = 2n. We have the orthonormal basis consisting of the vectors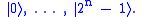
Each basis state index can be represented in binary form
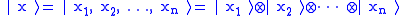
where
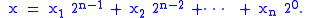
Similarly, we also adopt the notation
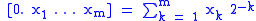 .
.For instance,
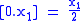 and
and 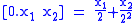 .
.With this notation, the action of the quantum Fourier transform can be expressed as:
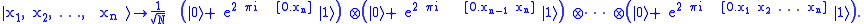
In other words, the discrete Fourier transform, an operation on n-qubits, can be factored into the tensor product of n single-qubit operations, suggesting it is easily represented as a quantum circuit
Quantum circuit
In quantum information theory, a quantum circuit is a model for quantum computation in which a computation is a sequence of quantum gates, which are reversible transformations on a quantum mechanical analog of an n-bit register...
. In fact, each of those single-qubit operations can be implemented efficiently using a Hadamard gate and controlled phase gates. The first term requires one Hadamard gate, the next one requires a Hadamard gate and a controlled phase gate, and each following term requires an additional controlled phase gate. Summing up the number of gates gives
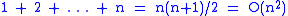 gates, which is polynomial in the number of qubits.
gates, which is polynomial in the number of qubits.Example
Consider the quantum Fourier transform on 3 qubits. It is the following transformation: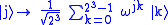 ,
,where
 is a primitive eighth root of unity
is a primitive eighth root of unityRoot of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
satisfying
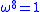 (since
(since 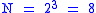 ).
).The matrix representing this transformation on 3 qubits is
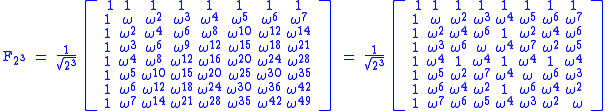 .
.The 3-qubit quantum Fourier transform is the following operation:
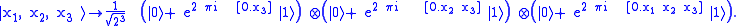
This quantum circuit implements the quantum Fourier transform on the quantum state
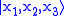 .
.The quantum gate
Quantum gate
In quantum computing and specifically the quantum circuit model of computation, a quantum gate is a basic quantum circuit operating on a small number of qubits. They are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.Unlike many classical...
s used in the circuit above are the Hadamard gate and the controlled phase gate
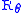 .
.As calculated above, the number of gates used is
 which is equal to 6, for n = 3.
which is equal to 6, for n = 3.

