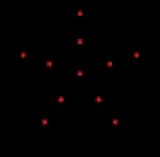
Grötzsch graph
Encyclopedia
In the mathematical
field of graph theory
, the Grötzsch graph is a triangle-free graph
with 11 vertices, 20 edges, and chromatic number 4. It is named after German mathematician Herbert Grötzsch
, and its existence demonstrates that the assumption of planarity is necessary in Grötzsch's theorem
(Grötzsch 1959) that every triangle-free planar graph
is 3-colorable. The Grötzsch graph is a member of an infinite sequence of triangle-free graphs, each the Mycielskian
of the previous graph in the sequence, starting from the null graph
; this sequence of graphs was used by to show that there exist triangle-free graphs with arbitrarily large chromatic number. Therefore, the Grötzsch graph is sometimes also called the Mycielski graph or the Mycielski–Grötzsch graph. Unlike later graphs in this sequence, the Grötzsch graph is the smallest triangle-free graph with its chromatic number .
used a modified version of the Grötzsch graph to disprove a conjecture of on the chromatic number of triangle-free graphs with high degree. Häggkvist's modification consists of replacing each of the five degree-four vertices of the Grötzsch graph by a set of three vertices, replacing each of the five degree-three vertices of the Grötzsch graph by a set of two vertices, and replacing the remaining degree-five vertex of the Grötzsch graph by a set of four vertices. Two vertices in this expanded graph are connected by an edge if they correspond to vertices connected by an edge in the Grötzsch graph. The result of Häggkvist's construction is a 10-regular
triangle-free graph with 29 vertices and chromatic number 4, disproving the conjecture that there is no 4-chromatic triangle-free n-vertex graph in which each vertex has more than n/3 neighbours.
The Grötzsch graph has chromatic index 5, radius 2, girth 4 and diameter 2. It is also a 3-vertex-connected
and 3-edge-connected
graph.
to the dihedral group
D5 of order 10, the group of symmetries of a regular pentagon, including both rotations and reflections.
The characteristic polynomial
of the Grötzsch graph is
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Grötzsch graph is a triangle-free graph
Triangle-free graph
In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
with 11 vertices, 20 edges, and chromatic number 4. It is named after German mathematician Herbert Grötzsch
Herbert Grötzsch
Camillo Herbert Grötzsch was a mathematician from Halle, Germany. Grötzsch worked in graph theory. He was the discoverer and eponym of the Grötzsch graph, a triangle-free graph that requires four colors in any graph coloring, and Grötzsch's theorem, the result that every triangle-free planar graph...
, and its existence demonstrates that the assumption of planarity is necessary in Grötzsch's theorem
Grötzsch's theorem
In the mathematical field of graph theory, Grötzsch's theorem is the statement that every triangle-free planar graph can be colored with only three colors...
(Grötzsch 1959) that every triangle-free planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
is 3-colorable. The Grötzsch graph is a member of an infinite sequence of triangle-free graphs, each the Mycielskian
Mycielskian
In the mathematical area of graph theory, the Mycielskian or Mycielski graph of an undirected graph G is a graph μ formed from G by a construction of , who used it to show that there exist triangle-free graphs with arbitrarily large chromatic number.-Construction:Let the n vertices of the given...
of the previous graph in the sequence, starting from the null graph
Null graph
In the mathematical field of graph theory, the null graph may refer either to the order zero graph, or alternatively, to any edgeless graph .-Order zero graph:...
; this sequence of graphs was used by to show that there exist triangle-free graphs with arbitrarily large chromatic number. Therefore, the Grötzsch graph is sometimes also called the Mycielski graph or the Mycielski–Grötzsch graph. Unlike later graphs in this sequence, the Grötzsch graph is the smallest triangle-free graph with its chromatic number .
used a modified version of the Grötzsch graph to disprove a conjecture of on the chromatic number of triangle-free graphs with high degree. Häggkvist's modification consists of replacing each of the five degree-four vertices of the Grötzsch graph by a set of three vertices, replacing each of the five degree-three vertices of the Grötzsch graph by a set of two vertices, and replacing the remaining degree-five vertex of the Grötzsch graph by a set of four vertices. Two vertices in this expanded graph are connected by an edge if they correspond to vertices connected by an edge in the Grötzsch graph. The result of Häggkvist's construction is a 10-regular
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
triangle-free graph with 29 vertices and chromatic number 4, disproving the conjecture that there is no 4-chromatic triangle-free n-vertex graph in which each vertex has more than n/3 neighbours.
The Grötzsch graph has chromatic index 5, radius 2, girth 4 and diameter 2. It is also a 3-vertex-connected
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
and 3-edge-connected
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
graph.
Algebraic properties
The full automorphism group of the Grötzsch graph is isomorphicGroup isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
D5 of order 10, the group of symmetries of a regular pentagon, including both rotations and reflections.
The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Grötzsch graph is