Depth-first search
Encyclopedia
Depth-first search is an algorithm
for traversing or searching a tree, tree structure
, or graph
. One starts at the root (selecting some node as the root in the graph case) and explores as far as possible along each branch before backtracking
.
A version of depth-first search was investigated in the 19th century by French mathematician Charles Pierre Trémaux as a strategy for solving mazes
.
, returning to the most recent node it hasn't finished exploring. In a non-recursive implementation, all freshly expanded nodes are added to a stack
for exploration.
and space
analysis of DFS differs according to its application area. In theoretical computer science, DFS is typically used to traverse an entire graph, and takes time O(V + E)
, linear in the size of the graph. In these applications it also uses space O(V) in the worst case to store the stack of vertices on the current search path as well as the set of already-visited vertices. Thus, in this setting, the time and space bounds are the same as for breadth-first search
and the choice of which of these two algorithms to use depends less on their complexity and more on the different properties of the vertex orderings the two algorithms produce.
For applications of DFS to search problems in artificial intelligence
, however, the graph to be searched is often either too large to visit in its entirety or even infinite, and DFS may suffer from non-termination when the length of a path in the search tree is infinite. Therefore, the search is only performed to a limited depth, and due to limited memory availability one typically does not use data structures that keep track of the set of all previously visited vertices. In this case, the time is still linear in the number of expanded vertices and edges (although this number is not the same as the size of the entire graph because some vertices may be searched more than once and others not at all) but the space complexity of this variant of DFS is only proportional to the depth limit, much smaller than the space needed for searching to the same depth using breadth-first search. For such applications, DFS also lends itself much better to heuristic methods of choosing a likely-looking branch. When an appropriate depth limit is not known a priori, iterative deepening depth-first search
applies DFS repeatedly with a sequence of increasing limits; in the artificial intelligence mode of analysis, with a branching factor
greater than one, iterative deepening increases the running time by only a constant factor over the case in which the correct depth limit is known due to the geometric growth of the number of nodes per level.
a depth-first search starting at A, assuming that the left edges in the shown graph are chosen before right edges, and assuming the search remembers previously-visited nodes and will not repeat them (since this is a small graph), will visit the nodes in the following order: A, B, D, F, E, C, G. The edges traversed in this search form a Trémaux tree
, a structure with important applications in graph theory
.
Performing the same search without remembering previously visited nodes results in visiting nodes in the order A, B, D, F, E, A, B, D, F, E, etc. forever, caught in the A, B, D, F, E cycle and never reaching C or G.
Iterative deepening
is one technique to avoid this infinite loop and would reach all nodes.
 The most natural result of a depth first search of a graph (if it is considered as a function
The most natural result of a depth first search of a graph (if it is considered as a function
rather than a procedure
) is a spanning tree
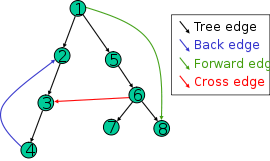
of the vertices reached during the search. Based on this spanning tree, the edges of the original graph can be divided into three classes: forward edges (or "discovery edges"), which point from a node of the tree to one of its descendants, back edges, which point from a node to one of its ancestors, and cross edges, which do neither. Sometimes tree edges, edges which belong to the spanning tree itself, are classified separately from forward edges. It can be shown that if the original graph is undirected then all of its edges are tree edges or back edges.
if (A) then {
B
} else {
C
}
D
Output: A labeling of the edges in the connected component of v as discovery edges and back edges
1 procedure DFS(G,v):
2 label v as explored
3 for all edges e in G.incidentEdges(v) do
4 if edge e is unexplored then
5 w ← G.opposite(v,e)
6 if vertex w is unexplored then
7 label e as a discovery edge
8 recursively call DFS(G,w)
9 else
10 label e as a back edge
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for traversing or searching a tree, tree structure
Tree structure
A tree structure is a way of representing the hierarchical nature of a structure in a graphical form. It is named a "tree structure" because the classic representation resembles a tree, even though the chart is generally upside down compared to an actual tree, with the "root" at the top and the...
, or graph
Graph (data structure)
In computer science, a graph is an abstract data structure that is meant to implement the graph and hypergraph concepts from mathematics.A graph data structure consists of a finite set of ordered pairs, called edges or arcs, of certain entities called nodes or vertices...
. One starts at the root (selecting some node as the root in the graph case) and explores as far as possible along each branch before backtracking
Backtracking
Backtracking is a general algorithm for finding all solutions to some computational problem, that incrementally builds candidates to the solutions, and abandons each partial candidate c as soon as it determines that c cannot possibly be completed to a valid solution.The classic textbook example...
.
A version of depth-first search was investigated in the 19th century by French mathematician Charles Pierre Trémaux as a strategy for solving mazes
Maze solving algorithm
There are a number of different maze solving algorithms, that is, automated methods for the solving of mazes. A few important maze solving algorithms are explained below...
.
Formal definition
Formally, DFS is an uninformed search that progresses by expanding the first child node of the search tree that appears and thus going deeper and deeper until a goal node is found, or until it hits a node that has no children. Then the search backtracksBacktracking
Backtracking is a general algorithm for finding all solutions to some computational problem, that incrementally builds candidates to the solutions, and abandons each partial candidate c as soon as it determines that c cannot possibly be completed to a valid solution.The classic textbook example...
, returning to the most recent node it hasn't finished exploring. In a non-recursive implementation, all freshly expanded nodes are added to a stack
Stack (data structure)
In computer science, a stack is a last in, first out abstract data type and linear data structure. A stack can have any abstract data type as an element, but is characterized by only three fundamental operations: push, pop and stack top. The push operation adds a new item to the top of the stack,...
for exploration.
Properties
The timeTime complexity
In computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...
and space
Memory management
Memory management is the act of managing computer memory. The essential requirement of memory management is to provide ways to dynamically allocate portions of memory to programs at their request, and freeing it for reuse when no longer needed. This is critical to the computer system.Several...
analysis of DFS differs according to its application area. In theoretical computer science, DFS is typically used to traverse an entire graph, and takes time O(V + E)
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
, linear in the size of the graph. In these applications it also uses space O(V) in the worst case to store the stack of vertices on the current search path as well as the set of already-visited vertices. Thus, in this setting, the time and space bounds are the same as for breadth-first search
Breadth-first search
In graph theory, breadth-first search is a graph search algorithm that begins at the root node and explores all the neighboring nodes...
and the choice of which of these two algorithms to use depends less on their complexity and more on the different properties of the vertex orderings the two algorithms produce.
For applications of DFS to search problems in artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
, however, the graph to be searched is often either too large to visit in its entirety or even infinite, and DFS may suffer from non-termination when the length of a path in the search tree is infinite. Therefore, the search is only performed to a limited depth, and due to limited memory availability one typically does not use data structures that keep track of the set of all previously visited vertices. In this case, the time is still linear in the number of expanded vertices and edges (although this number is not the same as the size of the entire graph because some vertices may be searched more than once and others not at all) but the space complexity of this variant of DFS is only proportional to the depth limit, much smaller than the space needed for searching to the same depth using breadth-first search. For such applications, DFS also lends itself much better to heuristic methods of choosing a likely-looking branch. When an appropriate depth limit is not known a priori, iterative deepening depth-first search
Iterative deepening depth-first search
Iterative deepening depth-first search is a state space search strategy in which a depth-limited search is run repeatedly, increasing the depth limit with each iteration until it reaches d, the depth of the shallowest goal state...
applies DFS repeatedly with a sequence of increasing limits; in the artificial intelligence mode of analysis, with a branching factor
Branching factor
In computing, tree data structures, and game theory, the branching factor is the number of children at each node. If this value is not uniform, an average branching factor can be calculated....
greater than one, iterative deepening increases the running time by only a constant factor over the case in which the correct depth limit is known due to the geometric growth of the number of nodes per level.
Example
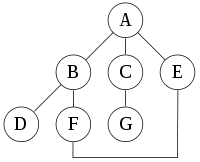
For the following graph:
a depth-first search starting at A, assuming that the left edges in the shown graph are chosen before right edges, and assuming the search remembers previously-visited nodes and will not repeat them (since this is a small graph), will visit the nodes in the following order: A, B, D, F, E, C, G. The edges traversed in this search form a Trémaux tree
Trémaux tree
In graph theory a Trémaux tree of a graph G is a spanning tree of G, rooted at one of its vertices, with the property that every edge in G connects a pair of vertices that are related as ancestor and descendant in the tree...
, a structure with important applications in graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
.
Performing the same search without remembering previously visited nodes results in visiting nodes in the order A, B, D, F, E, A, B, D, F, E, etc. forever, caught in the A, B, D, F, E cycle and never reaching C or G.
Iterative deepening
Iterative deepening depth-first search
Iterative deepening depth-first search is a state space search strategy in which a depth-limited search is run repeatedly, increasing the depth limit with each iteration until it reaches d, the depth of the shallowest goal state...
is one technique to avoid this infinite loop and would reach all nodes.
Output of a depth-first search

Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
rather than a procedure
Subroutine
In computer science, a subroutine is a portion of code within a larger program that performs a specific task and is relatively independent of the remaining code....
) is a spanning tree
Spanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
of the vertices reached during the search. Based on this spanning tree, the edges of the original graph can be divided into three classes: forward edges (or "discovery edges"), which point from a node of the tree to one of its descendants, back edges, which point from a node to one of its ancestors, and cross edges, which do neither. Sometimes tree edges, edges which belong to the spanning tree itself, are classified separately from forward edges. It can be shown that if the original graph is undirected then all of its edges are tree edges or back edges.
Vertex orderings
It is also possible to use the depth-first search to linearly order the vertices of the original graph (or tree). There are three common ways of doing this:- A preordering is a list of the vertices in the order that they were first visited by the depth-first search algorithm. This is a compact and natural way of describing the progress of the search, as was done earlier in this article. A preordering of an expression tree is the expression in Polish notationPolish notationPolish notation, also known as prefix notation, is a form of notation for logic, arithmetic, and algebra. Its distinguishing feature is that it places operators to the left of their operands. If the arity of the operators is fixed, the result is a syntax lacking parentheses or other brackets that...
.
- A postordering is a list of the vertices in the order that they were last visited by the algorithm. A postordering of an expression treeParse treeA concrete syntax tree or parse tree or parsing treeis an ordered, rooted tree that represents the syntactic structure of a string according to some formal grammar. In a parse tree, the interior nodes are labeled by non-terminals of the grammar, while the leaf nodes are labeled by terminals of the...
is the expression in reverse Polish notationReverse Polish notationReverse Polish notation is a mathematical notation wherein every operator follows all of its operands, in contrast to Polish notation, which puts the operator in the prefix position. It is also known as Postfix notation and is parenthesis-free as long as operator arities are fixed...
.
- A reverse postordering is the reverse of a postordering, i.e. a list of the vertices in the opposite order of their last visit. Reverse postordering is not the same as preordering. For example, when searching the directed graph
- beginning at node A, one visits the nodes in sequence, to produce lists either A B D B A C A, or A C D C A B A (depending upon whether the algorithm chooses to visit B or C first). Note that repeat visits in the form of backtracking to a node, to check if it has still unvisited neighbours, are included here (even if it is found to have none). Thus the possible preorderings are A B D C and A C D B (order by node's leftmost occurrence in above list), while the possible reverse postorderings are A C B D and A B C D (order by node's rightmost occurrence in above list). Reverse postordering produces a topological sortingTopological sortingIn computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that, for every edge uv, u comes before v in the ordering...
of any directed acyclic graphDirected acyclic graphIn mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
. This ordering is also useful in control flow analysisControl flow graphA control flow graph in computer science is a representation, using graph notation, of all paths that might be traversed through a program during its execution.- Overview :...
as it often represents a natural linearization of the control flow. The graph above might represent the flow of control in a code fragment like
if (A) then {
B
} else {
C
}
D
- and it is natural to consider this code in the order A B C D or A C B D, but not natural to use the order A B D C or A C D B.
Pseudocode
Input: A graph G and a vertex v of GOutput: A labeling of the edges in the connected component of v as discovery edges and back edges
1 procedure DFS(G,v):
2 label v as explored
3 for all edges e in G.incidentEdges(v) do
4 if edge e is unexplored then
5 w ← G.opposite(v,e)
6 if vertex w is unexplored then
7 label e as a discovery edge
8 recursively call DFS(G,w)
9 else
10 label e as a back edge
Applications
Algorithms that use depth-first search as a building block include:- Finding connected componentsConnected component (graph theory)In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
. - Topological sortingTopological sortingIn computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that, for every edge uv, u comes before v in the ordering...
. - Finding 2-(edge or vertex)-connected components.
- Finding 3-(edge or vertex)-connected components.
- Finding the bridges of a graph.
- Finding strongly connected components.
- Planarity TestingPlanarity testingIn graph theory, the planarity testing problem asks whether, given a graph, that graph is a planar graph . This is a well-studied problem in computer science for which many practical algorithms have emerged, many taking advantage of novel data structures...
- Solving puzzles with only one solution, such as mazeMazeA maze is a tour puzzle in the form of a complex branching passage through which the solver must find a route. In everyday speech, both maze and labyrinth denote a complex and confusing series of pathways, but technically the maze is distinguished from the labyrinth, as the labyrinth has a single...
s. (DFS can be adapted to find all solutions to a maze by only including nodes on the current path in the visited set.) - Maze generation may use a randomized depth-first search.
- Finding biconnectivity in graphsBiconnected graphIn the mathematical discipline of graph theory, a biconnected graph is a connected graph with no articulation vertices.In other words, a biconnected graph is connected and nonseparable, meaning that if any vertex were to be removed, the graph will remain connected.The property of being 2-connected...
.
External links
- Depth-First Explanation and Example
- C++ Boost Graph Library: Depth-First Search
- Depth-First Search Animation (for a directed graph)
- Depth First and Breadth First Search: Explanation and Code
- QuickGraph, depth first search example for .Net
- Depth-first search algorithm illustrated explanation (Java and C++ implementations)
- YAGSBPL - A template-based C++ library for graph search and planning