Topological sorting
Encyclopedia
In computer science
, a topological sort or topological ordering of a directed graph
is a linear ordering of its vertices
such that, for every edge uv, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph
(DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time.
technique for scheduling in project management . The jobs are represented by vertices, and there is an edge from x to y if job x must be completed before job y can be started (for example, when washing clothes, the washing machine must finish before we put the clothes to dry). Then, a topological sort gives an order in which to perform the jobs.
In computer science, applications of this type arise in instruction scheduling
, ordering of formula cell evaluation when recomputing formula values in spreadsheet
s, logic synthesis, determining the order of compilation tasks to perform in makefiles, and resolving symbol dependencies in linkers.
 ).
).
One of these algorithms, first described by , works by choosing vertices in the same order as the eventual topological sort. First, find a list of "start nodes" which have no incoming edges and insert them into a set S; at least one such node must exist in an acyclic graph. Then:
L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edges
while S is non-empty do
remove a node n from S
insert n into L
for each node m with an edge e from n to m do
remove edge e from the graph
if m has no other incoming edges then
insert m into S
if graph has edges then
output error message (graph has at least one cycle)
else
output message (proposed topologically sorted order: L)
If the graph were a DAG
, a solution is contained in the list L (the solution is not necessarily unique). Otherwise, the graph has at least one cycle and therefore a topological sorting is impossible.
Note that, reflecting the non-uniqueness of the resulting sort, the structure S can be simply a set or a queue or a stack. Depending on the order that nodes n are removed from set S, a different solution is created. A variation of Kahn's algorithm that breaks ties lexicographically forms a key component of the Coffman–Graham algorithm
for parallel scheduling and layered graph drawing
.
An alternative algorithm for topological sorting is based on depth-first search
. For this algorithm, the edges are examined in the opposite direction as the previous one (it looks for nodes with edges pointing to a given node instead of from it, which might set different requirements for the data structure used to represent the graph; and it starts with the set of nodes with no outgoing edges). The algorithm loops through each node of the graph, in an arbitrary order, initiating a depth-first search that terminates when it hits any node that has already been visited since the beginning of the topological sort:
L ← Empty list that will contain the sorted nodes
S ← Set of all nodes with no outgoing edges
for each node n in S do
visit(n)
function visit(node n)
if n has not been visited yet then
mark n as visited
for each node m with an edge from m to n do
visit(m)
add n to L
Note that each node n gets added to the output list L only after considering all other nodes on which n depends (all ancestor nodes of n in the graph). Specifically, when the algorithm adds node n, we are guaranteed that all nodes on which n depends are already in the output list L: they were added to L either by the preceding recursive call to visit, or by an earlier call to visit. Since each edge and node is visited once, the algorithm runs in linear time. Note that the simple pseudocode above cannot detect the error case where the input graph contains cycles. The algorithm can be refined to detect cycles by watching for nodes which are visited more than once during any nested sequence of recursive calls to visit (e.g., by passing a list down as an extra argument to visit, indicating which nodes have already been visited in the current call stack). This depth-first-search-based algorithm is the one described by ; it seems to have been first described in print by .
in the DAG. If a Hamiltonian path exists, the topological sort order is unique; no other order respects the edges of the path. Conversely, if a topological sort does not form a Hamiltonian path, the DAG will have two or more valid topological orderings, for in this case it is always possible to form a second valid ordering by swapping two consecutive vertices that are not connected by an edge to each other. Therefore, it is possible to test in polynomial time whether a unique ordering exists, and whether a Hamiltonian path exists, despite the NP-hard
ness of the Hamiltonian path problem for more general directed graphs .
of a partial order in mathematics.
A partially ordered set is just a set of objects together with a definition of the "≤" inequality relation, satisfying the axioms of asymmetry (x ≤ y and y ≤x if and only if x = y) and transitivity
(if x ≤ y and y ≤ z, then x ≤ z). A total order
is a partial order in which, for every two objects x and y in the set, either x ≤ y or y ≤ x. Total orders are familiar in computer science as the comparison operators needed to perform comparison sort
ing algorithms. For finite sets, total orders may be identified with linear sequences of objects, where the "≤" relation is true whenever the first object precedes the second object in the order; a comparison sorting algorithm may be used to convert a total order into a sequence in this way. A linear extension of a partial order is a total order that is compatible with it, in the sense that, if x ≤ y in the partial order, then x ≤ y in the total order as well.
One can define a partial ordering from any DAG by letting the set of objects be the vertices of the DAG, and defining x ≤ y to be true, for any two vertices x and y, whenever there exists a directed path from x to y; that is, whenever y is reachable
from x. With these definitions, a topological ordering of the DAG is the same thing as a linear extension of this partial order. Conversely, any partial ordering may be defined as the reachability relation in a DAG. One way of doing this is to define a DAG that has a vertex for every object in the partially ordered set, and an edge xy for every pair of objects for which x ≤ y. An alternative way of doing this is to use the transitive reduction
of the partial ordering; in general, this produces DAGs with fewer edges, but the reachability relation in these DAGs is still the same partial order. By using these constructions, one can use topological ordering algorithms to find linear extensions of partial orders.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a topological sort or topological ordering of a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
is a linear ordering of its vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
such that, for every edge uv, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
(DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time.
Examples
The canonical application of topological sorting (topological order) is in scheduling a sequence of jobs or tasks; topological sorting algorithms were first studied in the early 1960s in the context of the PERTProgram Evaluation and Review Technique
The Program ' Evaluation and Review Technique, commonly abbreviated PERT, is a statistical tool, used in project management, that is designed to analyze and represent the tasks involved in completing a given project...
technique for scheduling in project management . The jobs are represented by vertices, and there is an edge from x to y if job x must be completed before job y can be started (for example, when washing clothes, the washing machine must finish before we put the clothes to dry). Then, a topological sort gives an order in which to perform the jobs.
In computer science, applications of this type arise in instruction scheduling
Instruction scheduling
In computer science, instruction scheduling is a compiler optimization used to improve instruction-level parallelism, which improves performance on machines with instruction pipelines...
, ordering of formula cell evaluation when recomputing formula values in spreadsheet
Spreadsheet
A spreadsheet is a computer application that simulates a paper accounting worksheet. It displays multiple cells usually in a two-dimensional matrix or grid consisting of rows and columns. Each cell contains alphanumeric text, numeric values or formulas...
s, logic synthesis, determining the order of compilation tasks to perform in makefiles, and resolving symbol dependencies in linkers.
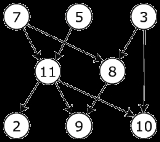
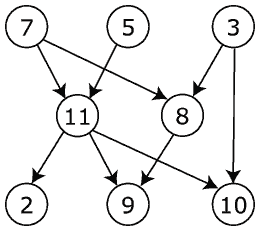 |
The graph shown to the left has many valid topological sorts, including:
|
Algorithms
The usual algorithms for topological sorting have running time linear in the number of nodes plus the number of edges ( ).
).One of these algorithms, first described by , works by choosing vertices in the same order as the eventual topological sort. First, find a list of "start nodes" which have no incoming edges and insert them into a set S; at least one such node must exist in an acyclic graph. Then:
L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edges
while S is non-empty do
remove a node n from S
insert n into L
for each node m with an edge e from n to m do
remove edge e from the graph
if m has no other incoming edges then
insert m into S
if graph has edges then
output error message (graph has at least one cycle)
else
output message (proposed topologically sorted order: L)
If the graph were a DAG
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
, a solution is contained in the list L (the solution is not necessarily unique). Otherwise, the graph has at least one cycle and therefore a topological sorting is impossible.
Note that, reflecting the non-uniqueness of the resulting sort, the structure S can be simply a set or a queue or a stack. Depending on the order that nodes n are removed from set S, a different solution is created. A variation of Kahn's algorithm that breaks ties lexicographically forms a key component of the Coffman–Graham algorithm
Coffman–Graham algorithm
In job shop scheduling and graph drawing, the Coffman–Graham algorithm is an algorithm, named after Edward G. Coffman, Jr. and Ronald Graham, for arranging the elements of a partially ordered set into a sequence of levels...
for parallel scheduling and layered graph drawing
Layered graph drawing
Layered graph drawing is a type of graph drawing in which the vertices of a directed graph are drawn in horizontal rows or layers with the edges generally directed downwards...
.
An alternative algorithm for topological sorting is based on depth-first search
Depth-first search
Depth-first search is an algorithm for traversing or searching a tree, tree structure, or graph. One starts at the root and explores as far as possible along each branch before backtracking....
. For this algorithm, the edges are examined in the opposite direction as the previous one (it looks for nodes with edges pointing to a given node instead of from it, which might set different requirements for the data structure used to represent the graph; and it starts with the set of nodes with no outgoing edges). The algorithm loops through each node of the graph, in an arbitrary order, initiating a depth-first search that terminates when it hits any node that has already been visited since the beginning of the topological sort:
L ← Empty list that will contain the sorted nodes
S ← Set of all nodes with no outgoing edges
for each node n in S do
visit(n)
function visit(node n)
if n has not been visited yet then
mark n as visited
for each node m with an edge from m to n do
visit(m)
add n to L
Note that each node n gets added to the output list L only after considering all other nodes on which n depends (all ancestor nodes of n in the graph). Specifically, when the algorithm adds node n, we are guaranteed that all nodes on which n depends are already in the output list L: they were added to L either by the preceding recursive call to visit, or by an earlier call to visit. Since each edge and node is visited once, the algorithm runs in linear time. Note that the simple pseudocode above cannot detect the error case where the input graph contains cycles. The algorithm can be refined to detect cycles by watching for nodes which are visited more than once during any nested sequence of recursive calls to visit (e.g., by passing a list down as an extra argument to visit, indicating which nodes have already been visited in the current call stack). This depth-first-search-based algorithm is the one described by ; it seems to have been first described in print by .
Uniqueness
If a topological sort has the property that all pairs of consecutive vertices in the sorted order are connected by edges, then these edges form a directed Hamiltonian pathHamiltonian path
In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle in an undirected graph that visits each vertex exactly once and also returns to the starting vertex...
in the DAG. If a Hamiltonian path exists, the topological sort order is unique; no other order respects the edges of the path. Conversely, if a topological sort does not form a Hamiltonian path, the DAG will have two or more valid topological orderings, for in this case it is always possible to form a second valid ordering by swapping two consecutive vertices that are not connected by an edge to each other. Therefore, it is possible to test in polynomial time whether a unique ordering exists, and whether a Hamiltonian path exists, despite the NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
ness of the Hamiltonian path problem for more general directed graphs .
Relation to partial orders
Topological orderings are also closely related to the concept of a linear extensionLinear extension
In order theory, a branch of mathematics, a linear extension of a partial order is a linear order that is compatible with the partial order.-Definitions:...
of a partial order in mathematics.
A partially ordered set is just a set of objects together with a definition of the "≤" inequality relation, satisfying the axioms of asymmetry (x ≤ y and y ≤x if and only if x = y) and transitivity
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
(if x ≤ y and y ≤ z, then x ≤ z). A total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
is a partial order in which, for every two objects x and y in the set, either x ≤ y or y ≤ x. Total orders are familiar in computer science as the comparison operators needed to perform comparison sort
Comparison sort
A comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation that determines which of two elements should occur first in the final sorted list...
ing algorithms. For finite sets, total orders may be identified with linear sequences of objects, where the "≤" relation is true whenever the first object precedes the second object in the order; a comparison sorting algorithm may be used to convert a total order into a sequence in this way. A linear extension of a partial order is a total order that is compatible with it, in the sense that, if x ≤ y in the partial order, then x ≤ y in the total order as well.
One can define a partial ordering from any DAG by letting the set of objects be the vertices of the DAG, and defining x ≤ y to be true, for any two vertices x and y, whenever there exists a directed path from x to y; that is, whenever y is reachable
Reachability
In graph theory, reachability is the notion of being able to get from one vertex in a directed graph to some other vertex. Note that reachability in undirected graphs is trivial — it is sufficient to find the connected components in the graph, which can be done in linear time.- Definition :For a...
from x. With these definitions, a topological ordering of the DAG is the same thing as a linear extension of this partial order. Conversely, any partial ordering may be defined as the reachability relation in a DAG. One way of doing this is to define a DAG that has a vertex for every object in the partially ordered set, and an edge xy for every pair of objects for which x ≤ y. An alternative way of doing this is to use the transitive reduction
Transitive reduction
In mathematics, a transitive reduction of a binary relation R on a set X is a minimal relation R' on X such that the transitive closure of R' is the same as the transitive closure of R. If the transitive closure of R is antisymmetric and finite, then R' is unique...
of the partial ordering; in general, this produces DAGs with fewer edges, but the reachability relation in these DAGs is still the same partial order. By using these constructions, one can use topological ordering algorithms to find linear extensions of partial orders.
See also
- tsortTsort (Unix)The tsort program is a command line utility on Unix-like platforms, that performs a topological sort on its input.-History:According to its info page, this command was initially written for providing an ordering of object files that allowed the linker to process them sequentially .Note that the...
, a Unix program for topological sorting - Feedback arc setFeedback arc setIn graph theory, a directed graph may contain directed cycles, a one-way loop of edges. In some applications, such cycles are undesirable, and we wish to eliminate them and obtain a directed acyclic graph . One way to do this is simply to drop edges from the graph to break the cycles...
, a (possibly empty) set of arcs which, if removed from the graph, make it possible to topologically sort it. Useful for dealing with graphs with cycles.

