Stack (data structure) - AbsoluteAstronomy.com

Computer science

Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...

, a stack is a last in, first out (LIFO) abstract data type

Abstract data type

In computing, an abstract data type is a mathematical model for a certain class of data structures that have similar behavior; or for certain data types of one or more programming languages that have similar semantics...

and linear data structure

Data structure

In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...

. A stack can have any abstract data type

Abstract data type

as an element

Element

- Chemistry, electronics, or the geosciences :* Chemical element, a building block in chemistry* Electrical element, an abstract part of a circuit* Heating element, a device that generates heat by electrical resistance...

, but is characterized by only three fundamental operations: push, pop and stack top. The push operation adds a new item to the top of the stack, or initializes the stack if it is empty. If the stack is full and does not contain enough space to accept the given item, the stack is then considered to be in an overflow

Stack overflow

In software, a stack overflow occurs when too much memory is used on the call stack. The call stack contains a limited amount of memory, often determined at the start of the program. The size of the call stack depends on many factors, including the programming language, machine architecture,...

state. The pop operation removes an item from the top of the stack. A pop either reveals previously concealed items, or results in an empty stack, but if the stack is empty then it goes into underflow state (It means no items are present in stack to be removed). The stack top operation gets the data from the top-most position and returns it to the user without deleting it. The same underflow state can also occur in stack top operation if stack is empty.

A stack is a restricted data structure, because only a small number of operations are performed on it. The nature of the pop and push operations also means that stack elements have a natural order. Elements are removed from the stack in the reverse order to the order of their addition: therefore, the lower elements are those that have been on the stack the longest.

History

The stack was first proposed in 1955, and then patented in 1957, by the German Friedrich L. Bauer

Friedrich L. Bauer

Friedrich Ludwig Bauer is a German computer scientist and professor emeritus at Technical University of Munich.-Life:...

. The same concept was developed independently, at around the same time, by the Australian Charles Leonard Hamblin

Charles Leonard Hamblin

Charles Leonard Hamblin was an Australian philosopher, logician, and computer pioneer, as well as a professor of philosophy at the Technical University of New South Wales in Sydney....

Abstract definition

A stack is a fundamental computer science

Computer science

data structure

Data structure

and can be defined in an abstract, implementation-free manner,
or it can be generally defined as,
Stack is a linear list of items in which all additions and deletion are restricted to one end that is Top.

This is a VDM (Vienna Development Method
Vienna Development Method
The Vienna Development Method is one of the longest-established Formal Methods for the development of computer-based systems. Originating in work done at IBM's Vienna Laboratory in the 1970s, it has grown to include a group of techniques and tools based on a formal specification language - the VDM...

) description of a stack:

Function signatures:
init: -> Stack
push: N x Stack -> Stack
top: Stack -> (N U ERROR)
remove: Stack -> Stack
isempty: Stack -> Boolean

(where N indicates an element (natural numbers in this case), and U indicates set union)

Semantics:
top(init) = ERROR
top(push(i,s)) = i
remove(init) = init
remove(push(i, s)) = s
isempty(init) = true
isempty(push(i, s)) = false

Inessential operations

In modern computer languages, the stack is usually implemented with more operations than just "push","pop" and "Stack Top". Some implementations have a function which returns the current number of items on the stack. Alternatively, some implementations have a function that just returns if the stack is empty. Another typical helper operation stack top (also known as peek) can return the current top element of the stack without removing it.

Implementation

In most high level languages, a stack can be easily implemented either through an array or a linked list

Linked list

In computer science, a linked list is a data structure consisting of a group of nodes which together represent a sequence. Under the simplest form, each node is composed of a datum and a reference to the next node in the sequence; more complex variants add additional links...

. What identifies the data structure as a stack in either case is not the implementation but the interface: the user is only allowed to pop or push items onto the array or linked list, with few other helper operations. The following will demonstrate both implementations, using C.

Array

The array implementation aims to create an array where the first element (usually at the zero-offset) is the bottom. That is, array[0] is the first element pushed onto the stack and the last element popped off. The program must keep track of the size, or the length of the stack. The stack itself can therefore be effectively implemented as a two-element structure in C:

typedef struct {
size_t size;
int items[STACKSIZE];
} STACK;

The push operation is used both to initialize the stack, and to store values to it. It is responsible for inserting (copying) the value into the ps->items[] array and for incrementing the element counter (ps->size). In a responsible C implementation, it is also necessary to check whether the array is already full to prevent an overrun

Buffer overflow

In computer security and programming, a buffer overflow, or buffer overrun, is an anomaly where a program, while writing data to a buffer, overruns the buffer's boundary and overwrites adjacent memory. This is a special case of violation of memory safety....

.

void push(STACK *ps, int x)
{
if (ps->size STACKSIZE) {
fputs("Error: stack overflow\n", stderr);
abort;
} else
ps->items[ps->size++] = x;
}

The pop operation is responsible for removing a value from the stack, and decrementing the value of ps->size. A responsible C implementation will also need to check that the array is not already empty.

int pop(STACK *ps)
{
if (ps->size 0){
fputs("Error: stack underflow\n", stderr);
abort;
} else
return ps->items[--ps->size];
}

If we use a dynamic array

Dynamic array

In computer science, a dynamic array, growable array, resizable array, dynamic table, or array list is a random access, variable-size list data structure that allows elements to be added or removed...

, then we can implement a stack that can grow or shrink as much as needed. The size of the stack is simply the size of the dynamic array. A dynamic array is a very efficient implementation of a stack, since adding items to or removing items from the end of a dynamic array is amortized O(1) time.

Linked list

The linked-list implementation is equally simple and straightforward. In fact, a simple singly linked list is sufficient to implement a stack—it only requires that the head node or element can be removed, or popped, and a node can only be inserted by becoming the new head node.

Unlike the array implementation, our structure typedef corresponds not to the entire stack structure, but to a single node:

typedef struct stack {
int data;
struct stack *next;
} STACK;

Such a node is identical to a typical singly linked list node, at least to those that are implemented in C.

The push operation both initializes an empty stack, and adds a new node to a non-empty one. It works by receiving a data value to push onto the stack, along with a target stack, creating a new node by allocating memory for it, and then inserting it into a linked list as the new head:

void push(STACK **head, int value)
{
STACK *node = malloc(sizeof(STACK)); /* create a new node */

if (node NULL){
fputs("Error: no space available for node\n", stderr);
abort;
} else { /* initialize node */
node->data = value;
node->next = empty(*head) ? NULL : *head; /* insert new head if any */
*head = node;
}
}

A pop operation removes the head from the linked list, and assigns the pointer to the head to the previous second node. It checks whether the list is empty before popping from it:

int pop(STACK **head)
{
if (empty(*head)) { /* stack is empty */
fputs("Error: stack underflow\n", stderr);
abort;
} else { /* pop a node */
STACK *top = *head;
int value = top->data;
*head = top->next;
free(top);
return value;
}
}

Stacks and programming languages

Some languages, like LISP and Python

Python (programming language)

Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...

, do not call for stack implementations, since push and pop functions are available for any list. All Forth-like languages (such as Adobe PostScript

PostScript

PostScript is a dynamically typed concatenative programming language created by John Warnock and Charles Geschke in 1982. It is best known for its use as a page description language in the electronic and desktop publishing areas. Adobe PostScript 3 is also the worldwide printing and imaging...

) are also designed around language-defined stacks that are directly visible to and manipulated by the programmer.

C++'s Standard Template Library

Standard Template Library

The Standard Template Library is a C++ software library which later evolved into the C++ Standard Library. It provides four components called algorithms, containers, functors, and iterators. More specifically, the C++ Standard Library is based on the STL published by SGI. Both include some...

provides a "stack" templated class which is restricted to only push/pop operations. Java's library contains a class that is a specialization of ---this could be considered a design flaw, since the inherited get method from ignores the LIFO constraint of the . PHP has an SplStack class.
Hardware stacks
A common use of stacks at the architecture level is as a means of allocating and accessing memory.

Basic architecture of a stack

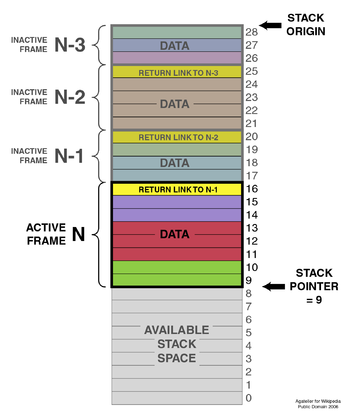
A typical stack is an area of computer memory with a fixed origin and a variable size. Initially the size of the stack is zero. A stack pointer, usually in the form of a hardware register, points to the most recently referenced location on the stack; when the stack has a size of zero, the stack pointer points to the origin of the stack.

The two operations applicable to all stacks are:

a push operation, in which a data item is placed at the location pointed to by the stack pointer, and the address in the stack pointer is adjusted by the size of the data item;
a pop or pull operation: a data item at the current location pointed to by the stack pointer is removed, and the stack pointer is adjusted by the size of the data item.

There are many variations on the basic principle of stack operations. Every stack has a fixed location in memory at which it begins. As data items are added to the stack, the stack pointer is displaced to indicate the current extent of the stack, which expands away from the origin.

Stack pointers may point to the origin of a stack or to a limited range of addresses either above or below the origin (depending on the direction in which the stack grows); however, the stack pointer cannot cross the origin of the stack. In other words, if the origin of the stack is at address 1000 and the stack grows downwards (towards addresses 999, 998, and so on), the stack pointer must never be incremented beyond 1000 (to 1001, 1002, etc.). If a pop operation on the stack causes the stack pointer to move past the origin of the stack, a stack underflow occurs. If a push operation causes the stack pointer to increment or decrement beyond the maximum extent of the stack, a stack overflow occurs.

Some environments that rely heavily on stacks may provide additional operations, for example:

Dup(licate): the top item is popped, and then pushed again (twice), so that an additional copy of the former top item is now on top, with the original below it.
Peek: the topmost item is inspected (or returned), but the stack pointer is not changed, and the stack size does not change (meaning that the item remains on the stack). This is also called top operation in many articles.
Swap or exchange: the two topmost items on the stack exchange places.
Rotate (or Roll): the n topmost items are moved on the stack in a rotating fashion. For example, if n=3, items 1, 2, and 3 on the stack are moved to positions 2, 3, and 1 on the stack, respectively. Many variants of this operation are possible, with the most common being called left rotate and right rotate.

Stacks are either visualized growing from the bottom up (like real-world stacks), or, with the top of the stack in a fixed position (see image [note in the image, the top (28) is the stack 'bottom', since the stack 'top' is where items are pushed or popped from]), a coin holder, a Pez

PEZ

Pez is the brand name of an Austrian confectionery and the mechanical pocket dispensers for the same...

dispenser, or growing from left to right, so that "topmost" becomes "rightmost". This visualization may be independent of the actual structure of the stack in memory. This means that a right rotate will move the first element to the third position, the second to the first and the third to the second. Here are two equivalent visualizations of this process:

apple banana
banana

right rotate> cucumber
cucumber apple

cucumber apple
banana

left rotate> cucumber
apple banana

A stack is usually represented in computers by a block of memory cells, with the "bottom" at a fixed location, and the stack pointer holding the address of the current "top" cell in the stack. The top and bottom terminology are used irrespective of whether the stack actually grows towards lower memory addresses or towards higher memory addresses.

Pushing an item on to the stack adjusts the stack pointer by the size of the item (either decrementing or incrementing, depending on the direction in which the stack grows in memory), pointing it to the next cell, and copies the new top item to the stack area. Depending again on the exact implementation, at the end of a push operation, the stack pointer may point to the next unused location in the stack, or it may point to the topmost item in the stack. If the stack points to the current topmost item, the stack pointer will be updated before a new item is pushed onto the stack; if it points to the next available location in the stack, it will be updated after the new item is pushed onto the stack.

Popping the stack is simply the inverse of pushing. The topmost item in the stack is removed and the stack pointer is updated, in the opposite order of that used in the push operation.

Stack in main memory

Most CPUs

Central processing unit

The central processing unit is the portion of a computer system that carries out the instructions of a computer program, to perform the basic arithmetical, logical, and input/output operations of the system. The CPU plays a role somewhat analogous to the brain in the computer. The term has been in...

have registers that can be used as stack pointers. Processor families like the x86, Z80, 6502, and many others have special instructions that implicitly use a dedicated (hardware) stack pointer to conserve opcode space. Some processors, like the PDP-11

PDP-11

The PDP-11 was a series of 16-bit minicomputers sold by Digital Equipment Corporation from 1970 into the 1990s, one of a succession of products in the PDP series. The PDP-11 replaced the PDP-8 in many real-time applications, although both product lines lived in parallel for more than 10 years...

and the 68000, also have special addressing modes for implementation of stacks, typically with a semi-dedicated stack pointer as well (such as A7 in the 68000). However, in most processors, several different registers may be used as additional stack pointers as needed (whether updated via addressing modes or via add/sub instructions).

Stack in registers or dedicated memory

The x87

X87

x87 is a floating point-related subset of the x86 architecture instruction set. It originated as an extension of the 8086 instruction set in the form of optional floating point coprocessors that worked in tandem with corresponding x86 CPUs. These microchips had names ending in "87"...

floating point

Floating point

In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...

architecture is an example of a set of registers organised as a stack where direct access to individual registers (relative the current top) is also possible. As with stack-based machines in general, having the top-of-stack as an implicit argument allows for a small machine code

Machine code

Machine code or machine language is a system of impartible instructions executed directly by a computer's central processing unit. Each instruction performs a very specific task, typically either an operation on a unit of data Machine code or machine language is a system of impartible instructions...

footprint with a good usage of bus bandwidth

Bandwidth (computing)

In computer networking and computer science, bandwidth, network bandwidth, data bandwidth, or digital bandwidth is a measure of available or consumed data communication resources expressed in bits/second or multiples of it .Note that in textbooks on wireless communications, modem data transmission,...

and code caches, but it also prevents some types of optimizations possible on processors permitting random access

Random access

In computer science, random access is the ability to access an element at an arbitrary position in a sequence in equal time, independent of sequence size. The position is arbitrary in the sense that it is unpredictable, thus the use of the term "random" in "random access"...

to the register file

A register file is an array of processor registers in a central processing unit . Modern integrated circuit-based register files are usually implemented by way of fast static RAMs with multiple ports...

for all (two or three) operands. A stack structure also makes superscalar

Superscalar

A superscalar CPU architecture implements a form of parallelism called instruction level parallelism within a single processor. It therefore allows faster CPU throughput than would otherwise be possible at a given clock rate...

implementations with register renaming

In computer architecture, register renaming refers to a technique used to avoid unnecessary serialization of program operations imposed by the reuse of registers by those operations.-Problem definition:...

(for speculative execution

Speculative execution

Speculative execution in computer systems is doing work, the result of which may not be needed. This performance optimization technique is used in pipelined processors and other systems.-Main idea:...

) somewhat more complex to implement, although it is still feasible, as exemplified by modern x87

X87

implementations.

Sun SPARC, AMD Am29000

AMD Am29000

The AMD 29000, often simply 29k, was a popular family of 32-bit RISC microprocessors and microcontrollers developed and fabricated by Advanced Micro Devices . They were, for a time, the most popular RISC chips on the market, widely used in laser printers from a variety of manufacturers...

, and Intel i960

Intel i960

Intel's i960 was a RISC-based microprocessor design that became popular during the early 1990s as an embedded microcontroller, becoming a best-selling CPU in that field, along with the competing AMD 29000...

are all examples of architectures using register window

In computer engineering, the use of register windows is a technique to improve the performance of a particularly common operation, the procedure call...

s within a register-stack as another strategy to avoid the use of slow main memory for function arguments and return values.

There are also a number of small microprocessors that implements a stack directly in hardware and some microcontroller

Microcontroller

A microcontroller is a small computer on a single integrated circuit containing a processor core, memory, and programmable input/output peripherals. Program memory in the form of NOR flash or OTP ROM is also often included on chip, as well as a typically small amount of RAM...

s have a fixed-depth stack that is not directly accessible. Examples are the PIC microcontroller

PIC microcontroller

PIC is a family of Harvard architecture microcontrollers made by Microchip Technology, derived from the PIC1650 originally developed by General Instrument's Microelectronics Division...

s, the Computer Cowboys MuP21, the Harris RTX line, and the Novix NC4016. Many stack-based microprocessors were used to implement the programming language Forth at the microcode

Microcode

Microcode is a layer of hardware-level instructions and/or data structures involved in the implementation of higher level machine code instructions in many computers and other processors; it resides in special high-speed memory and translates machine instructions into sequences of detailed...

level. Stacks were also used as a basis of a number of mainframes and mini computers. Such machines were called stack machine

Stack machine

A stack machine may be* A real or emulated computer that evaluates each sub-expression of a program statement via a pushdown data stack and uses a reverse Polish notation instruction set....

s, the most famous being the Burroughs B5000.
Applications

Stacks have numerous applications. We see stacks in everyday life, from the books in our library, to the sheaf of papers that we keep in our printer tray. All of them follow the Last In First Out (LIFO) logic, that is when we add a book to a pile of books, we add it to the top of the pile, whereas when we remove a book from the pile, we generally remove it from the top of the pile.
Given below are a few applications of stacks in the world of computers:

Converting a decimal number into a binary number

The logic for transforming a decimal number into a binary number is as follows:

Read a number
Iteration (while number is greater than zero)
1. Find out the remainder after dividing the number by 2
2. Print the remainder
3. Divide the number by 2
End the iteration

However, there is a problem with this logic. Suppose the number, whose binary form we want to find is 23. Using this logic, we get the result as 11101, instead of getting 10111.

To solve this problem, we use a stack. We make use of the LIFO property of the stack. Initially we push the binary digit formed into the stack, instead of printing it directly. After the entire digit has been converted into the binary form, we pop one digit at a time from the stack and print it. Therefore we get the decimal number is converted into its proper binary form.

Algorithm:
function outputInBinary(Integer n)
Stack s = new Stack
while n > 0 do
Integer bit = n modulo
Modulo operation
In computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...

2
s.push(bit)
if s is full then
return error
end if
n = floor(n / 2)
end while
while s is not empty do
output(s.pop)
end while
end function

Towers of Hanoi

One of the most interesting applications of stacks can be found in solving a puzzle called Tower of Hanoi. According to an old Brahmin story, the existence of the universe is calculated in terms of the time taken by a number of monks, who are working all the time, to move 64 disks from one pole to another. But there are some rules about how this should be done, which are:

You can move only one disk at a time.
For temporary storage, a third pole may be used.
You cannot place a disk of larger diameter on a disk of smaller diameter.

For algorithm of this puzzle see Tower of Hanoi.

Here we assume that A is first tower, B is second tower & C is third tower.
Output : (when there are 3 disks)

Let 1 be the smallest disk, 2 be the disk of medium size and 3 be the largest disk.

Move disk	From peg	To peg
1	A	C
2	A	B
1	C	B
3	A	C
1	B	A
2	B	C
1	A	C

The C++ code for this solution can be implemented in two ways:

First Implementation (Without using Stacks)

void TowersofHanoi(int n, int a, int b, int c)
{
if(n > 0)
{
TowersofHanoi(n-1, a, c, b); //recursion
cout << " Move top disk from tower " <<
a << " to tower " << b << endl ;
TowersofHanoi(n-1, c, b, a); //recursion
}
}

Second Implementation (Using Stacks)

// Global variable , tower [1:3] are three towers
arrayStack tower[4];

void TowerofHanoi(int n)
{
// Preprocessor for moveAndShow.
for (int d = n; d > 0; d--) //initialize
tower[1].push(d); //add disk d to tower 1
moveAndShow(n, 1, 2, 3); /*move n disks from tower 1 to tower 3 using
tower 2 as intermediate tower*/
}

void moveAndShow(int n, int a, int b, int c)
{
// Move the top n disks from tower a to tower b showing states.
// Use tower c for intermediate storage.
if(n > 0)
{
moveAndShow(n-1, a, c, b); //recursion
int d = tower[x].top; //move a disc from top of tower x to top of
tower[x].pop; //tower y
tower[y].push(d);
showState; //show state of 3 towers
moveAndShow(n-1, c, b, a); //recursion
}
}

However complexity

Computational complexity theory

Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...

for above written implementations is O(

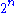). So it's obvious that problem can only be solved for small values of n (generally n <= 30).
In case of the monks, the number of turns taken to transfer 64 disks, by following the above rules, will be 18,446,744,073,709,551,615; which will surely take a lot of time!

Expression evaluation and syntax parsing

Calculators employing reverse Polish notation

Reverse Polish notation

Reverse Polish notation is a mathematical notation wherein every operator follows all of its operands, in contrast to Polish notation, which puts the operator in the prefix position. It is also known as Postfix notation and is parenthesis-free as long as operator arities are fixed...

use a stack structure to hold values. Expressions can be represented in prefix, postfix or infix notations and conversion from one form to another may be accomplished using a stack. Many compilers use a stack for parsing the syntax of expressions, program blocks etc. before translating into low level code. Most programming languages are context-free languages

Context-free grammar

In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....

, allowing them to be parsed with stack based machines.

Evaluation of an Infix Expression that is Fully Parenthesized

Input: (((2 * 5) - (1 * 2)) / (11 - 9))

Output: 4

Analysis: Five types of input characters
* Opening bracket
* Numbers
* Operators
* Closing bracket
* New line character

Data structure requirement: A character stack

Algorithm
1. Read one input character
2. Actions at end of each input
Opening brackets (2.1) Push into stack and then Go to step (1)
Number (2.2) Push into stack and then Go to step (1)
Operator (2.3) Push into stack and then Go to step (1)
Closing brackets (2.4) Pop from character stack
(2.4.1) if it is closing bracket, then discard it, Go to step (1)
(2.4.2) Pop is used three times
The first popped element is assigned to op2
The second popped element is assigned to op
The third popped element is assigned to op1
Evaluate op1 op op2
Convert the result into character and
push into the stack
Go to step (2.4)
New line character (2.5) Pop from stack and print the answer
STOP

Result: The evaluation of the fully parenthesized infix expression is printed as follows:

Input String: (((2 * 5) - (1 * 2)) / (11 - 9))

Input Symbol	Stack (from bottom to top)	Operation
(	(
(	( (
(	( ( (
2	( ( ( 2
*	( ( ( 2 *
5		( ( ( 2 * 5
)	( ( 10	2 * 5 = 10 and push
-	( ( 10 -
(	( ( 10 - (
1	( ( 10 - ( 1
*	( ( 10 - ( 1 *
2	( ( 10 - ( 1 * 2
)	( ( 10 - 2	1 * 2 = 2 & Push
)	( 8	10 - 2 = 8 & Push
/	( 8 /
(	( 8 / (
11	( 8 / ( 11
-	( 8 / ( 11 -
9	( 8 / ( 11 - 9
)	( 8 / 2	11 - 9 = 2 & Push
)	4	8 / 2 = 4 & Push
New line	Empty	Pop & Print

Evaluation of Infix Expression which is not fully parenthesized

Input: (2 * 5 - 1 * 2) / (11 - 9)

Output: 4

Analysis: There are five types of input characters which are:
* Opening brackets
* Numbers
* Operators
* Closing brackets
* New line character (\n)

We do not know what to do if an operator is read as an input character.
By implementing the priority rule for operators, we have a solution to this problem.

The Priority rule: we should perform a comparative priority check if an operator is read, and then push it. If the stack top contains an operator of priority higher than or equal to the priority of the input operator, then we pop it and print it. We keep on performing the priority check until the top of stack either contains an operator of lower priority or if it does not contain an operator.

Data Structure Requirement for this problem: A character stack and an integer stack

Algorithm:

1. Read an input character
2. Actions that will be performed at the end of each input
Opening brackets (2.1) Push it into character stack and then Go to step (1)
Digit (2.2) Push into integer stack, Go to step (1)
Operator (2.3) Do the comparative priority check
(2.3.1) if the character stack's top contains an operator with equal
or higher priority, then pop it into op
Pop a number from integer stack into op2
Pop another number from integer stack into op1
Calculate op1 op op2 and push the result into the integer
stack
Closing brackets (2.4) Pop from the character stack
(2.4.1) if it is an opening bracket, then discard it and Go to
step (1)
(2.4.2) To op, assign the popped element
Pop a number from integer stack and assign it op2
Pop another number from integer stack and assign it
to op1
Calculate op1 op op2 and push the result into the integer
stack
Convert into character and push into stack
Go to the step (2.4)
New line character (2.5) Print the result after popping from the stack
STOP

Result: The evaluation of an infix expression that is not fully parenthesized is printed as follows:

Input String: (2 * 5 - 1 * 2) / (11 - 9)

Input Symbol	Character Stack (from bottom to top)	Integer Stack (from bottom to top)	Operation performed
(	(
2	(	2
*	( *		Push as * has higher priority
5	( *	2 5
-	( *		Since '-' has less priority, we do 2 * 5 = 10
	( -	10	We push 10 and then push '-'
1	( -	10 1
*	( - *	10 1	Push * as it has higher priority
2	( - *	10 1 2
)	( -	10 2	Perform 1 * 2 = 2 and push it
	(	8	Pop - and 10 - 2 = 8 and push, Pop (
/	/	8
(	/ (	8
11	/ (	8 11
-	/ ( -	8 11
9	/ ( -	8 11 9
)	/	8 2	Perform 11 - 9 = 2 and push it
New line		4	Perform 8 / 2 = 4 and push it
		4	Print the output, which is 4

Evaluation of Prefix Expression

Input: / - 2 5 * 1 2 - 11 9

Output: 4

Analysis: There are three types of input characters
* Numbers
* Operators
* New line character (\n)

Data structure requirement: A character stack and an integer stack

Algorithm:

1. Read one character input at a time and keep pushing it into the character stack until the new
line character is reached
2. Perform pop from the character stack. If the stack is empty, go to step (3)
Number (2.1) Push in to the integer stack and then go to step (1)
Operator (2.2) Assign the operator to op
Pop a number from integer stack and assign it to op1
Pop another number from integer stack
and assign it to op2
Calculate op1 op op2 and push the output into the integer
stack. Go to step (2)
3. Pop the result from the integer stack and display the result

Result: The evaluation of prefix expression is printed as follows:

Input String: / - * 2 5 * 1 2 - 11 9

Input Symbol	Character Stack (from bottom to top)	Integer Stack (from bottom to top)	Operation performed
/	/
-	/
*	/ - *
2	/ - * 2
5	/ - * 2 5
*	/ - * 2 5 *
1	/ - * 2 5 * 1
2	/ - * 2 5 * 1 2
-	/ - * 2 5 * 1 2 -
11	/ - * 2 5 * 1 2 - 11
9	/ - * 2 5 * 1 2 - 11 9
\n	/ - * 2 5 * 1 2 - 11	9
	/ - * 2 5 * 1 2 -	9 11
	/ - * 2 5 * 1 2	2	11 - 9 = 2
	/ - * 2 5 * 1	2 2
	/ - * 2 5 *	2 2 1
	/ - * 2 5	2 2	1 * 2 = 2
	/ - * 2	2 2 5
	/ - *	2 2 5 2
	/ -	2 2 10	5 * 2 = 10
	/	2 8	10 - 2 = 8
	Stack is empty	4	8 / 2 = 4
		Stack is empty	Print 4

Evaluation of postfix expression

The calculation: 1 + 2 * 4 + 3 can be written down like this in postfix notation with the advantage of no precedence rules and parentheses needed:

1 2 4 * + 3 +
The expression is evaluated from the left to right using a stack:

when encountering an operand: push it
when encountering an operator
Operator (programming)
Programming languages typically support a set of operators: operations which differ from the language's functions in calling syntax and/or argument passing mode. Common examples that differ by syntax are mathematical arithmetic operations, e.g...

: pop two operands, evaluate the result and push it.

Like the following way (the Stack is displayed after Operation has taken place):

Input	Operation	Stack (after op)
1	Push operand	1
2	Push operand	2, 1
4	Push operand	4, 2, 1
*	Multiply	8, 1
+	Add	9
3	Push operand	3, 9
+	Add	12

The final result, 12, lies on the top of the stack at the end of the calculation.

Example in C

include

int main
{
int a[100], i;
printf("To pop enter -1\n");
for(i = 0;;)
{
printf("Push ");
scanf("%d", &a[i]);
if(a[i] -1)
{
if(i 0)
{
printf("Underflow\n");
}
else
{
printf("pop = %d\n", a[--i]);
}
}
else
{
i++;
}
}
}

Evaluation of postfix expression (Pascal)

This is an implementation in Pascal

Pascal (programming language)

Pascal is an influential imperative and procedural programming language, designed in 1968/9 and published in 1970 by Niklaus Wirth as a small and efficient language intended to encourage good programming practices using structured programming and data structuring.A derivative known as Object Pascal...

, using marked sequential file as data archives.

{
programmer : clx321
file : stack.pas
unit : Pstack.tpu
}
program TestStack;
{this program uses ADT of Stack, I will assume that the unit of ADT of Stack has already existed}

uses
PStack; {ADT of STACK}

{dictionary}
const
mark = '.';

var
data : stack;
f : text;
cc : char;
ccInt, cc1, cc2 : integer;

{functions}
IsOperand (cc : char) : boolean; {JUST Prototype}
{return TRUE if cc is operand}
ChrToInt (cc : char) : integer; {JUST Prototype}
{change char to integer}
Operator (cc1, cc2 : integer) : integer; {JUST Prototype}
{operate two operands}

{algorithms}
begin
assign (f, cc);
reset (f);
read (f, cc); {first elmt}
if (cc = mark) then
begin
writeln ('empty archives !');
end
else
begin
repeat
if (IsOperand (cc)) then
begin
ccInt := ChrToInt (cc);
push (ccInt, data);
end
else
begin
pop (cc1, data);
pop (cc2, data);
push (data, Operator (cc2, cc1));
end;
read (f, cc); {next elmt}
until (cc = mark);
end;
close (f);
end

}

Conversion of an Infix expression that is fully parenthesized into a Postfix expression

Input: (((8 + 1) - (7 - 4)) / (11 - 9))

Output: 8 1 + 7 4 - - 11 9 - /

Analysis: There are five types of input characters which are:
* Opening brackets
* Numbers
* Operators
* Closing brackets
* New line character (\n)

Requirement: A character stack

Algorithm:

1. Read an character input
2. Actions to be performed at end of each input
Opening brackets (2.1) Push into stack and then Go to step (1)
Number (2.2) Print and then Go to step (1)
Operator (2.3) Push into stack and then Go to step (1)
Closing brackets (2.4) Pop it from the stack
(2.4.1) If it is an operator, print it, Go to step (1)
(2.4.2) If the popped element is an opening bracket,
discard it and go to step (1)
New line character (2.5) STOP

Therefore, the final output after conversion of an infix expression to a postfix expression is as follows:

Input	Operation	Stack (after op)	Output on monitor
(	(2.1) Push operand into stack	(
(	(2.1) Push operand into stack	( (
(	(2.1) Push operand into stack	( ( (
8	(2.2) Print it		8
+	(2.3) Push operator into stack	( ( ( +	8
1	(2.2) Print it		8 1
)	(2.4) Pop from the stack: Since popped element is '+' print it	( ( (	8 1 +
	(2.4) Pop from the stack: Since popped element is '(' we ignore it and read next character	( (	8 1 +
-	(2.3) Push operator into stack	( ( -
(	(2.1) Push operand into stack	( ( - (
7	(2.2) Print it		8 1 + 7
-	(2.3) Push the operator in the stack	( ( - ( -
4	(2.2) Print it		8 1 + 7 4
)	(2.4) Pop from the stack: Since popped element is '-' print it	( ( - (	8 1 + 7 4 -
	(2.4) Pop from the stack: Since popped element is '(' we ignore it and read next character	( ( -
)	(2.4) Pop from the stack: Since popped element is '-' print it	( (	8 1 + 7 4 - -
	(2.4) Pop from the stack: Since popped element is '(' we ignore it and read next character	(
/	(2.3) Push the operand into the stack	( /
(	(2.1) Push into the stack	( / (
11	(2.2) Print it		8 1 + 7 4 - - 11
-	(2.3) Push the operand into the stack	( / ( -
9	(2.2) Print it		8 1 + 7 4 - - 11 9
)	(2.4) Pop from the stack: Since popped element is '-' print it	( / (	8 1 + 7 4 - - 11 9 -
	(2.4) Pop from the stack: Since popped element is '(' we ignore it and read next character	( /
)	(2.4) Pop from the stack: Since popped element is '/' print it	(	8 1 + 7 4 - - 11 9 - /
	(2.4) Pop from the stack: Since popped element is '(' we ignore it and read next character	Stack is empty
New line character	(2.5) STOP

Problem Description

This is one useful application of stacks. Consider that a freight train has n railroad cars, each to be left at different station. They're numbered 1 through n and freight train visits these stations in order n through 1. Obviously, the railroad cars are labeled by their destination. To facilitate removal of the cars from the train, we must rearrange them in ascending order of their number (i.e. 1 through n). When cars are in this order, they can be detached at each station. We rearrange cars at a shunting yard that has input track, output track and k holding tracks between input & output tracks (i.e. holding track).

Solution Strategy

To rearrange cars, we examine the cars on the input from front to back. If the car being examined is next one in the output arrangement , we move it directly to output track. If not , we move it to the holding track & leave it there until it's time to place it to the output track. The holding tracks operate in a LIFO manner as the cars enter & leave these tracks from top. When rearranging cars only following moves are permitted:

A car may be moved from front (i.e. right end) of the input track to the top of one of the holding tracks or to the left end of the output track.
A car may be moved from the top of holding track to left end of the output track.

The figure shows a shunting yard with k = 3, holding tracks H1, H2 & H3, also n = 9. The n cars of freight train begin in the input track & are to end up in the output track in order 1 through n from right to left. The cars initially are in the order 5,8,1,7,4,2,9,6,3 from back to front. Later cars are rearranged in desired order.

A Three Track Example

Consider the input arrangement from figure , here we note that the car 3 is at the front, so it can't be output yet, as it to be preceded by cars 1 & 2. So car 3 is detached & moved to holding track H1.
The next car 6 can't be output & it is moved to holding track H2. Because we have to output car 3 before car 6 & this will not possible if we move car 6 to holding track H1.
Now it's obvious that we move car 9 to H3.

The requirement of rearrangement of cars on any holding track is that the cars should be preferred to arrange in ascending order from top to bottom.

So car 2 is now moved to holding track H1 so that it satisfies the previous statement. If we move car 2 to H2 or H3, then we've no place to move cars 4,5,7,8.The least restrictions on future car placement arise when the new car λ is moved to the holding track that has a car at its top with smallest label Ψ such that λ < Ψ. We may call it an assignment rule to decide whether a particular car belongs to a specific holding track.
When car 4 is considered, there are three places to move the car H1,H2,H3. The top of these tracks are 2,6,9.So using above mentioned Assignment rule, we move car 4 to H2.
The car 7 is moved to H3.
The next car 1 has the least label, so it's moved to output track.
Now it's time for car 2 & 3 to output which are from H1(in short all the cars from H1 are appended to car 1 on output track).

The car 4 is moved to output track. No other cars can be moved to output track at this time.

The next car 8 is moved to holding track H1.
Car 5 is output from input track. Car 6 is moved to output track from H2, so is the 7 from H3,8 from H1 & 9 from H3.

Quicksort

Sorting means arranging the list of elements in a particular order. In case of numbers, it could be in ascending order, or in the case of letters, alphabetic order.

Quicksort is an algorithm of the divide and conquer type. In this method, to sort a set of numbers, we reduce it to two smaller sets, and then sort these smaller sets.

This can be explained with the help of the following example:

Suppose A is a list of the following numbers:
In the reduction step, we find the final position of one of the numbers. In this case, let us assume that we have to find the final position of 48, which is the first number in the list.

To accomplish this, we adopt the following method. Begin with the last number, and move from right to left. Compare each number with 48. If the number is smaller than 48, we stop at that number and swap it with 48.
In our case, the number is 24. Hence, we swap 24 and 48.
The numbers 96 and 72 to the right of 48, are greater than 48. Now beginning with 24, scan the numbers in the opposite direction, that is from left to right. Compare every number with 48 until you find a number that is greater than 48.

In this case, it is 60. Therefore we swap 48 and 60.
Note that the numbers 12, 24 and 36 to the left of 48 are all smaller than 48. Now, start scanning numbers from 60, in the right to left direction. As soon as you find lesser number, swap it with 48.

In this case, it is 44. Swap it with 48. The final result is:
Now, beginning with 44, scan the list from left to right, until you find a number greater than 48.

Such a number is 84. Swap it with 48. The final result is:
Now, beginning with 84, traverse the list from right to left, until you reach a number lesser than 48. We do not find such a number before reaching 48. This means that all the numbers in the list have been scanned and compared with 48. Also, we notice that all numbers less than 48 are to the left of it, and all numbers greater than 48, are to its right.

The final partitions look as follows:
Therefore, 48 has been placed in its proper position and now our task is reduced to sorting the two partitions.
This above step of creating partitions can be repeated with every partition containing 2 or more elements. As we can process only a single partition at a time, we should be able to keep track of the other partitions, for future processing.

This is done by using two stacks called LOWERBOUND and UPPERBOUND, to temporarily store these partitions. The addresses of the first and last elements of the partitions are pushed into the LOWERBOUND and UPPERBOUND stacks respectively. Now, the above reduction step is applied to the partitions only after it's boundary values are popped from the stack.

We can understand this from the following example:

Take the above list A with 12 elements. The algorithm starts by pushing the boundary values of A, that is 1 and 12 into the LOWERBOUND and UPPERBOUND stacks respectively. Therefore the stacks look as follows:

LOWERBOUND: 1 UPPERBOUND: 12

To perform the reduction step, the values of the stack top are popped from the stack. Therefore, both the stacks become empty.

LOWERBOUND: {empty} UPPERBOUND: {empty}

Now, the reduction step causes 48 to be fixed to the 5th position and creates two partitions, one from position 1 to 4 and the other from position 6 to 12. Hence, the values 1 and 6 are pushed into the LOWERBOUND stack and 4 and 12 are pushed into the UPPERBOUND stack.

LOWERBOUND: 1, 6 UPPERBOUND: 4, 12

For applying the reduction step again, the values at the stack top are popped. Therefore, the values 6 and 12 are popped. Therefore the stacks look like:

LOWERBOUND: 1 UPPERBOUND: 4

The reduction step is now applied to the second partition, that is from the 6th to 12th element.
After the reduction step, 98 is fixed in the 11th position. So, the second partition has only one element. Therefore, we push the upper and lower boundary values of the first partition onto the stack. So, the stacks are as follows:

LOWERBOUND: 1, 6 UPPERBOUND: 4, 10

The processing proceeds in the following way and ends when the stacks do not contain any upper and lower bounds of the partition to be processed, and the list gets sorted.

The Stock Span Problem

In the stock span problem, we will solve a financial problem with the help of stacks.

Suppose, for a stock, we have a series of n daily price quotes, the span of the stock's price on a particular day is defined as the maximum number of consecutive days for which the price of the stock on the current day is less than or equal to its price on that day.

An algorithm which has Quadratic Time Complexity

Input: An array P with n elements

Output: An array S of n elements such that P[i] is the largest integer k such that k <= i + 1 and P[y] <= P[i] for j = i - k + 1,.....,i

Algorithm:

1. Initialize an array P which contains the daily prices of the stocks
2. Initialize an array S which will store the span of the stock
3. for i = 0 to i = n - 1
3.1 Initialize k to zero
3.2 Done with a false condition
3.3 repeat
3.3.1 if ( P[i - k] <= P[i)] then
Increment k by 1
3.3.2 else
Done with true condition
3.4 Till (k > i) or done with processing
Assign value of k to S[i] to get the span of the stock
4. Return array S

Now, analyzing this algorithm for running time, we observe:

We have initialized the array S at the beginning and returned it at the end. This is a constant time operation, hence takes O(n) time

The repeat loop is nested within the for loop. The for loop, whose counter is i is executed n times. The statements which are not in the repeat loop, but in the for loop are executed n times. Therefore these statements and the incrementing and condition testing of i take O(n) time.

In repetition of i for the outer for loop, the body of the inner repeat loop is executed maximum i + 1 times. In the worst case, element S[i] is greater than all the previous elements. So, testing for the if condition, the statement after that, as well as testing the until condition, will be performed i + 1 times during iteration i for the outer for loop. Hence, the total time taken by the inner loop is O(n(n + 1)/2), which is O()

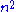The running time of all these steps is calculated by adding the time taken by all these three steps. The first two terms are O(

) while the last term is O(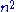

). Therefore the total running time of the algorithm is O(

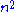An algorithm which has Linear Time Complexity

In order to calculate the span more efficiently, we see that the span on a particular day can be easily calculated if we know the closest day before i , such that the price of the stocks on that day was higher than the price of the stocks on the present day. If there exists such a day, we can represent it by h(i) and initialize h(i) to be -1.

Therefore the span of a particular day is given by the formula,
s = i - h(i).

To implement this logic, we use a stack as an abstract data type to store the days i, h(i), h(h(i)) and so on. When we go from day i-1 to i, we pop the days when the price of the stock was less than or equal to p(i) and then push the value of day i back into the stack.

Here, we assume that the stack is implemented by operations that take O(1) that is constant time. The algorithm is as follows:

Input: An array P with n elements and an empty stack N

Output: An array S of n elements such that P[i] is the largest integer k such that k <= i + 1 and P[y] <= P[i] for j = i - k + 1,.....,i

Algorithm:

1. Initialize an array P which contains the daily prices of the stocks
2. Initialize an array S which will store the span of the stock
3. for i = 0 to i = n - 1
3.1 Initialize k to zero
3.2 Done with a false condition
3.3 while not (Stack N is empty or done with processing)
3.3.1 if ( P[i] >= P[N.top)] then
Pop a value from stack N
3.3.2 else
Done with true condition
3.4 if Stack N is empty
3.4.1 Initialize h to -1
3.5 else
3.5.1 Initialize stack top to h
3.5.2 Put the value of h - i in S[i]
3.5.3 Push the value of i in N
4. Return array S

Now, analyzing this algorithm for running time, we observe:

We have initialized the array S at the beginning and returned it at the end. This is a constant time operation, hence takes O(n) time

The while loop is nested within the for loop. The for loop, whose counter is i is executed n times. The statements which are not in the repeat loop, but in the for loop are executed n times. Therefore these statements and the incrementing and condition testing of i take O(n) time.

Now, observe the inner while loop during i repetitions of the for loop. The statement done with a true condition is done at most once, since it causes an exit from the loop. Let us say that t(i) is the number of times statement Pop a value from stack N is executed. So it becomes clear that while not (Stack N is empty or done with processing) is tested maximum t(i) + 1 times.

Adding the running time of all the operations in the while loop, we get:

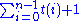
An element once popped from the stack N is never pushed back into it. Therefore,

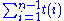
So, the running time of all the statements in the while loop is O(

)

The running time of all the steps in the algorithm is calculated by adding the time taken by all these steps. The run time of each step is O(

). Hence the running time complexity of this algorithm is O(

Runtime memory management

A number of programming language

Programming language

A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....

s are stack-oriented

Stack-oriented programming language

A stack-oriented programming language is one that relies on a stack machine model for passing parameters. Several programming languages fit this description, notably Forth, RPL, PostScript, and also many Assembly languages ....

, meaning they define most basic operations (adding two numbers, printing a character) as taking their arguments from the stack, and placing any return values back on the stack. For example, PostScript

PostScript

has a return stack and an operand stack, and also has a graphics state stack and a dictionary stack.

Forth uses two stacks, one for argument passing and one for subroutine return address

Return address

In postal mail, a return address is an explicit inclusion of the address of the person sending the message. It provides the recipient with a means to determine how to respond to the sender of the message if needed....

es. The use of a return stack is extremely commonplace, but the somewhat unusual use of an argument stack for a human-readable programming language is the reason Forth is referred to as a stack-based
Stack-oriented programming language
A stack-oriented programming language is one that relies on a stack machine model for passing parameters. Several programming languages fit this description, notably Forth, RPL, PostScript, and also many Assembly languages ....

language.

Many virtual machine

Virtual machine

A virtual machine is a "completely isolated guest operating system installation within a normal host operating system". Modern virtual machines are implemented with either software emulation or hardware virtualization or both together.-VM Definitions:A virtual machine is a software...

s are also stack-oriented, including the p-code machine

P-Code machine

In computer programming, a p-code machine, or portable code machine is a virtual machine designed to execute p-code...

and the Java Virtual Machine

Java Virtual Machine

A Java virtual machine is a virtual machine capable of executing Java bytecode. It is the code execution component of the Java software platform. Sun Microsystems stated that there are over 4.5 billion JVM-enabled devices.-Overview:...

.

Almost all calling convention

Calling convention

In computer science, a calling convention is a scheme for how subroutines receive parameters from their caller and how they return a result; calling conventions can differ in:...

s -- computer runtime memory environments—use a special stack (the "call stack

Call stack

In computer science, a call stack is a stack data structure that stores information about the active subroutines of a computer program. This kind of stack is also known as an execution stack, control stack, run-time stack, or machine stack, and is often shortened to just "the stack"...

") to hold information about procedure/function calling and nesting in order to switch to the context of the called function and restore to the caller function when the calling finishes. The functions follow a runtime protocol between caller and callee to save arguments and return value on the stack. Stacks are an important way of supporting nested or recursive

Recursion

Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...

function calls. This type of stack is used implicitly by the compiler to support CALL and RETURN statements (or their equivalents) and is not manipulated directly by the programmer.

Some programming languages use the stack to store data that is local to a procedure. Space for local data items is allocated from the stack when the procedure is entered, and is deallocated when the procedure exits. The C programming language

C (programming language)

C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....

is typically implemented in this way. Using the same stack for both data and procedure calls has important security implications (see below) of which a programmer must be aware in order to avoid introducing serious security bugs into a program.
Security
Some computing environments use stacks in ways that may make them vulnerable to security breaches and attacks. Programmers working in such environments must take special care to avoid the pitfalls of these implementations.

For example, some programming languages use a common stack to store both data local to a called procedure and the linking information that allows the procedure to return to its caller. This means that the program moves data into and out of the same stack that contains critical return addresses for the procedure calls. If data is moved to the wrong location on the stack, or an oversized data item is moved to a stack location that is not large enough to contain it, return information for procedure calls may be corrupted, causing the program to fail.

Malicious parties may attempt a stack smashing attack that takes advantage of this type of implementation by providing oversized data input to a program that does not check the length of input. Such a program may copy the data in its entirety to a location on the stack, and in so doing it may change the return addresses for procedures that have called it. An attacker can experiment to find a specific type of data that can be provided to such a program such that the return address of the current procedure is reset to point to an area within the stack itself (and within the data provided by the attacker), which in turn contains instructions that carry out unauthorized operations.

This type of attack is a variation on the buffer overflow

Buffer overflow

attack and is an extremely frequent source of security breaches in software, mainly because some of the most popular programming languages (such as C

C (programming language)

C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....

) use a shared stack for both data and procedure calls, and do not verify the length of data items. Frequently programmers do not write code to verify the size of data items, either, and when an oversized or undersized data item is copied to the stack, a security breach may occur.
See also

List of data structures

Queue

Double-ended queue

Call stack
Call stack
In computer science, a call stack is a stack data structure that stores information about the active subroutines of a computer program. This kind of stack is also known as an execution stack, control stack, run-time stack, or machine stack, and is often shortened to just "the stack"...

Stack-based memory allocation
Stack-based memory allocation
Stacks in computing architectures are regions of memory where data is added or removed in a last-in-first-out manner.In most modern computer systems, each thread has a reserved region of memory referred to as its stack. When a function executes, it may add some of its state data to the top of the...

Stack machine
Stack machine
A stack machine may be* A real or emulated computer that evaluates each sub-expression of a program statement via a pushdown data stack and uses a reverse Polish notation instruction set....

History

Abstract definition

Inessential operations

Implementation

Array

Linked list

Stacks and programming languages

Basic architecture of a stack

right rotate> cucumber cucumber apple cucumber apple banana

Stack in main memory

Stack in registers or dedicated memory

Converting a decimal number into a binary number

Towers of Hanoi

First Implementation (Without using Stacks)

Second Implementation (Using Stacks)

Expression evaluation and syntax parsing

Evaluation of an Infix Expression that is Fully Parenthesized

Evaluation of Infix Expression which is not fully parenthesized

Evaluation of Prefix Expression

Evaluation of postfix expression

Evaluation of postfix expression (Pascal)

Conversion of an Infix expression that is fully parenthesized into a Postfix expression

Problem Description

Solution Strategy

A Three Track Example

Quicksort

The Stock Span Problem

An algorithm which has Quadratic Time Complexity

An algorithm which has Linear Time Complexity

Runtime memory management

right rotate> cucumber
cucumber apple

cucumber apple
banana