Polyhedral combinatorics
Encyclopedia
Polyhedral combinatorics is a branch of mathematics
, within combinatorics
and discrete geometry
, that studies the problems of counting and describing the faces of convex polyhedra and higher dimensional convex polytope
s.
Research in polyhedral combinatorics falls into two distinct areas. Mathematicians in this area study the combinatorics
of polytopes; for instance, they seek inequalities that describe the relations between the numbers of vertices, edges, and faces of higher dimensions in arbitrary polytopes or in certain important subclasses of polytopes, and study other combinatorial properties of polytopes such as their connectivity
and diameter
(number of steps needed to reach any vertex from any other vertex). Additionally, many computer scientists use the phrase “polyhedral combinatorics” to describe research into precise descriptions of the faces of certain specific polytopes (especially 0-1 polytopes, whose vertices are subsets of a hypercube
) arising from integer programming
problems.
A face of a convex polytope P may be defined as the intersection of P and a closed halfspace H such that the boundary of H contains no interior point of P. The dimension of a face is the dimension of this hull. The 0-dimensional faces are the vertices themselves, and the 1-dimensional faces (called edges) are line segment
s connecting pairs of vertices. Note that this definition also includes as faces the empty set and the whole polytope P. If P itself has dimension d, the faces of P with dimension d − 1 are called facets of P and the faces with dimension d − 2 are called ridges. The faces of P may be partially ordered by inclusion, forming a face lattice that has as its top element P itself and as its bottom element the empty set.
A key tool in polyhedral combinatorics is the ƒ-vector of a polytope, the vector (f0, f1, ..., fd − 1) where fi is the number of i-dimensional features of the polytope. For instance, a cube
has eight vertices, twelve edges, and six facets, so its ƒ-vector is (8,12,6). The dual polytope
has a ƒ-vector with the same numbers in the reverse order; thus, for instance, the regular octahedron, the dual to a cube, has the ƒ-vector (6,12,8). The extended ƒ-vector is formed by concatenating the number one at each end of the ƒ-vector, counting the number of objects at all levels of the face lattice; on the left side of the vector, f-1 = 1 counts the empty set as a face, while on the right side, fd = 1 counts P itself.
For the cube the extended ƒ-vector is (1,8,12,6,1) and for the octahedron it is (1,6,12,8,1). Although the vectors for these example polyhedra are unimodal (the coefficients, taken in left to right order, increase to a maximum and then decrease), there are higher dimensional polytopes for which this is not true.
For simplicial polytope
s (polytopes in which every facet is a simplex
), it is often convenient to transform these vectors, producing a different vector called the h-vector. If we interpret the terms of the ƒ-vector (omitting the final 1) as coefficients of a polynomial ƒ(x) = Σfixd − i − 1 (for instance, for the octahedron this gives the polynomial ƒ(x) = x3 + 6x2 + 12x + 8), then the h-vector lists the coefficients of the polynomial h(x) = ƒ(x − 1) (again, for the octahedron, h(x) = x3 + 3x2 + 3x + 1). As Ziegler writes, “for various problems about simplicial polytopes, h-vectors are a much more convenient and concise way to encode the information about the face numbers than ƒ-vectors.”
Σ(−1)ifi = 0, where the terms of the sum range over the coefficients of the extended ƒ-vector. In three dimensions, moving the two 1's at the left and right ends of the extended ƒ-vector (1, v, e, f, 1) to the right hand side of the equation transforms this identity into the more familiar form v − e + f = 2. From the fact that each facet of a three-dimensional polyhedron has at least three edges, it follows by double counting
that 2e ≥ 3f, and using this inequality to eliminate e and f from Euler's formula leads to the further inequalities e ≤ 3v − 6 and f ≤ 2v − 4. By duality, e ≤ 3f − 6 and v ≤ 2f − 4. It follows from Steinitz's theorem
that any 3-dimensional integer vector satisfying these equalities and inequalities is the ƒ-vector of a convex polyhedron.
In higher dimensions, other relations among the numbers of faces of a polytope become important as well, including the Dehn–Sommerville equations which, expressed in terms of h-vectors
of simplicial polytopes, take the simple form hk = hd − k for all k. The instance of these equations with k = 0 is equivalent to Euler's formula but for d > 3 the other instances of these equations are linearly independent of each other and constrain the h-vectors (and therefore also the ƒ-vectors) in additional ways.
Another important inequality on polytope face counts is given by the Upper Bound Conjecture, first proven by , which states that a d-dimensional polytopes with n vertices can have at most as many faces of any other dimension as a neighborly polytope
with the same number of vertices:
where the asterisk means that the final term of the sum should be halved when d is even. Asymptotically, this implies that there are at most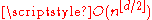
faces of all dimensions.
Even in four dimensions, the set of possible ƒ-vectors of convex polytopes does not form a convex subset of the four-dimensional integer lattice, and much remains unknown about the possible values of these vectors.
).
Balinski's theorem
states that the graph obtained in this way from any d-dimensional convex polytope is d-vertex-connected
. In the case of three-dimensional polyhedra, this property and planarity
may be used to exactly characterize the graphs of polyhedra: Steinitz's theorem
states that G is the skeleton of a three-dimensional polyhedron if and only if G is a 3-vertex-connected planar graph.
A theorem of Blind and Mani states that one can reconstruct the face structure of a simple polytope
from its graph. This is in sharp contrast with (non-simple) neighborly polytopes whose graph is a complete graph
. An elegant proof is due to Kalai
and a polynomial time algorithm to recognize a face was recently found by Friedman.
In the context of the simplex method for linear programming
, it is important to understand the diameter
of a polytope, the minimum number of edges needed to reach any vertex by a path from any other vertex. The system of linear inequalities
of a linear program define facets of a polytope representing all feasible solutions to the program, and the simplex method finds the optimal solution by following a path in this polytope. Thus, the diameter provides a lower bound on the number of steps this method requires.
s for integer programming
to be able to describe accurately the facets of polytopes that have vertices corresponding to the solutions of combinatorial optimization problems. Often, these problems have solutions that can be described by binary vectors, and the corresponding polytopes have vertex coordinates that are all zero or one.
As an example, consider the Birkhoff polytope, the set of n × n matrices that can be formed from convex combination
s of permutation matrices. Equivalently, its vertices can be thought of as describing all perfect matchings in a complete bipartite graph
, and a linear optimization problem on this polytope can be interpreted as a bipartite minimum weight perfect matching problem. The Birkhoff-von Neumann theorem states that this polytope can be described by two types of linear inequality or equality. First, for each matrix cell, there is a constraint that this cell has a non-negative value. And second, for each row or column of the matrix, there is a constraint that the sum of the cells in that row or column equal one. The row and column constraints define a linear subspace of dimension n2 − 2n + 1 in which the Birkhoff polytope lies, and the non-negativity constraints define facets of the Birkhoff polytope within that subspace.
However, the Birkhoff polytope is unusual in that a complete description of its facets is available. For many other 0-1 polytopes, there are exponentially many or superexponentially many facets, and only partial descriptions of their facets are available.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, within combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and discrete geometry
Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
, that studies the problems of counting and describing the faces of convex polyhedra and higher dimensional convex polytope
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
s.
Research in polyhedral combinatorics falls into two distinct areas. Mathematicians in this area study the combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
of polytopes; for instance, they seek inequalities that describe the relations between the numbers of vertices, edges, and faces of higher dimensions in arbitrary polytopes or in certain important subclasses of polytopes, and study other combinatorial properties of polytopes such as their connectivity
Connectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
and diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
(number of steps needed to reach any vertex from any other vertex). Additionally, many computer scientists use the phrase “polyhedral combinatorics” to describe research into precise descriptions of the faces of certain specific polytopes (especially 0-1 polytopes, whose vertices are subsets of a hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
) arising from integer programming
Integer programming
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming, which is also known as mixed integer programming.Integer programming is NP-hard...
problems.
Faces and face-counting vectors
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
s connecting pairs of vertices. Note that this definition also includes as faces the empty set and the whole polytope P. If P itself has dimension d, the faces of P with dimension d − 1 are called facets of P and the faces with dimension d − 2 are called ridges. The faces of P may be partially ordered by inclusion, forming a face lattice that has as its top element P itself and as its bottom element the empty set.
A key tool in polyhedral combinatorics is the ƒ-vector of a polytope, the vector (f0, f1, ..., fd − 1) where fi is the number of i-dimensional features of the polytope. For instance, a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
has eight vertices, twelve edges, and six facets, so its ƒ-vector is (8,12,6). The dual polytope
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
has a ƒ-vector with the same numbers in the reverse order; thus, for instance, the regular octahedron, the dual to a cube, has the ƒ-vector (6,12,8). The extended ƒ-vector is formed by concatenating the number one at each end of the ƒ-vector, counting the number of objects at all levels of the face lattice; on the left side of the vector, f-1 = 1 counts the empty set as a face, while on the right side, fd = 1 counts P itself.
For the cube the extended ƒ-vector is (1,8,12,6,1) and for the octahedron it is (1,6,12,8,1). Although the vectors for these example polyhedra are unimodal (the coefficients, taken in left to right order, increase to a maximum and then decrease), there are higher dimensional polytopes for which this is not true.
For simplicial polytope
Simplicial polytope
In geometry, a simplicial polytope is a d-polytope whose facets are all simplices.For example, a simplicial polyhedron contains only triangular faces and corresponds via Steinitz's theorem to a maximal planar graph....
s (polytopes in which every facet is a simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
), it is often convenient to transform these vectors, producing a different vector called the h-vector. If we interpret the terms of the ƒ-vector (omitting the final 1) as coefficients of a polynomial ƒ(x) = Σfixd − i − 1 (for instance, for the octahedron this gives the polynomial ƒ(x) = x3 + 6x2 + 12x + 8), then the h-vector lists the coefficients of the polynomial h(x) = ƒ(x − 1) (again, for the octahedron, h(x) = x3 + 3x2 + 3x + 1). As Ziegler writes, “for various problems about simplicial polytopes, h-vectors are a much more convenient and concise way to encode the information about the face numbers than ƒ-vectors.”
Equalities and inequalities
The most important relation among the coefficients of the ƒ-vector of a polytope is Euler's formulaEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
Σ(−1)ifi = 0, where the terms of the sum range over the coefficients of the extended ƒ-vector. In three dimensions, moving the two 1's at the left and right ends of the extended ƒ-vector (1, v, e, f, 1) to the right hand side of the equation transforms this identity into the more familiar form v − e + f = 2. From the fact that each facet of a three-dimensional polyhedron has at least three edges, it follows by double counting
Double counting (proof technique)
In combinatorics, double counting, also called counting in two ways, is a combinatorial proof technique for showing that two expressions are equal by demonstrating that they are two ways of counting the size of one set...
that 2e ≥ 3f, and using this inequality to eliminate e and f from Euler's formula leads to the further inequalities e ≤ 3v − 6 and f ≤ 2v − 4. By duality, e ≤ 3f − 6 and v ≤ 2f − 4. It follows from Steinitz's theorem
Steinitz's theorem
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
that any 3-dimensional integer vector satisfying these equalities and inequalities is the ƒ-vector of a convex polyhedron.
In higher dimensions, other relations among the numbers of faces of a polytope become important as well, including the Dehn–Sommerville equations which, expressed in terms of h-vectors
H-vector
In algebraic combinatorics, the h-vector of a simplicial polytope is a fundamental invariant of the polytope which encodes the number of faces of different dimensions and allows one to express the Dehn–Sommerville equations in a particularly simple form...
of simplicial polytopes, take the simple form hk = hd − k for all k. The instance of these equations with k = 0 is equivalent to Euler's formula but for d > 3 the other instances of these equations are linearly independent of each other and constrain the h-vectors (and therefore also the ƒ-vectors) in additional ways.
Another important inequality on polytope face counts is given by the Upper Bound Conjecture, first proven by , which states that a d-dimensional polytopes with n vertices can have at most as many faces of any other dimension as a neighborly polytope
Neighborly polytope
In geometry and polyhedral combinatorics, a k-neighborly polytope is a convex polytope in which every set of k or fewer vertices forms a face. For instance, a 2-neighborly polytope is a polytope in which every pair of vertices is connected by an edge, forming a complete graph...
with the same number of vertices:
where the asterisk means that the final term of the sum should be halved when d is even. Asymptotically, this implies that there are at most
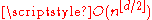faces of all dimensions.Even in four dimensions, the set of possible ƒ-vectors of convex polytopes does not form a convex subset of the four-dimensional integer lattice, and much remains unknown about the possible values of these vectors.
Graph-theoretic properties
Along with investigating the numbers of faces of polytopes, researchers have studied other combinatorial properties of them, such as descriptions of the graphs obtained from the vertices and edges of polytopes (their 1-skeletaN-skeleton
In mathematics, particularly in algebraic topology, the n-skeleton of a topological space X presented as a simplicial complex refers to the subspace Xn that is the union of the simplices of X of dimensions m ≤ n...
).
Balinski's theorem
Balinski's theorem
In polyhedral combinatorics, a branch of mathematics, Balinski's theorem is a statement about the graph-theoretic structure of three-dimensional polyhedra and higher-dimensional polytopes...
states that the graph obtained in this way from any d-dimensional convex polytope is d-vertex-connected
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
. In the case of three-dimensional polyhedra, this property and planarity
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
may be used to exactly characterize the graphs of polyhedra: Steinitz's theorem
Steinitz's theorem
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
states that G is the skeleton of a three-dimensional polyhedron if and only if G is a 3-vertex-connected planar graph.
A theorem of Blind and Mani states that one can reconstruct the face structure of a simple polytope
Simple polytope
In geometry, a d-dimensional simple polytope is a d-dimensional polytope each of whose vertices are adjacent to exactly d edges . The vertex figure of a simple d-polytope is a -simplex....
from its graph. This is in sharp contrast with (non-simple) neighborly polytopes whose graph is a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
. An elegant proof is due to Kalai
Gil Kalai
Gil Kalai is the Henry and Manya Noskwith Professor of Mathematics at the Hebrew University of Jerusalem, and adjunct professor of mathematics and of computer science at Yale University, and the editor of the Israel Journal of Mathematics.-Biography:...
and a polynomial time algorithm to recognize a face was recently found by Friedman.
In the context of the simplex method for linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
, it is important to understand the diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of a polytope, the minimum number of edges needed to reach any vertex by a path from any other vertex. The system of linear inequalities
Linear inequality
In mathematics a linear inequality is an inequality which involves a linear function.-Definitions:When two expressions are connected by 'greater than' or 'less than' sign, we get an inequation....
of a linear program define facets of a polytope representing all feasible solutions to the program, and the simplex method finds the optimal solution by following a path in this polytope. Thus, the diameter provides a lower bound on the number of steps this method requires.
Facets of 0-1 polytopes
It is important in the context of cutting-plane methodCutting-plane method
In mathematical optimization, the cutting-plane method is an umbrella term for optimization methods which iteratively refine a feasible set or objective function by means of linear inequalities, termed cuts...
s for integer programming
Integer programming
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming, which is also known as mixed integer programming.Integer programming is NP-hard...
to be able to describe accurately the facets of polytopes that have vertices corresponding to the solutions of combinatorial optimization problems. Often, these problems have solutions that can be described by binary vectors, and the corresponding polytopes have vertex coordinates that are all zero or one.
As an example, consider the Birkhoff polytope, the set of n × n matrices that can be formed from convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
s of permutation matrices. Equivalently, its vertices can be thought of as describing all perfect matchings in a complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
, and a linear optimization problem on this polytope can be interpreted as a bipartite minimum weight perfect matching problem. The Birkhoff-von Neumann theorem states that this polytope can be described by two types of linear inequality or equality. First, for each matrix cell, there is a constraint that this cell has a non-negative value. And second, for each row or column of the matrix, there is a constraint that the sum of the cells in that row or column equal one. The row and column constraints define a linear subspace of dimension n2 − 2n + 1 in which the Birkhoff polytope lies, and the non-negativity constraints define facets of the Birkhoff polytope within that subspace.
However, the Birkhoff polytope is unusual in that a complete description of its facets is available. For many other 0-1 polytopes, there are exponentially many or superexponentially many facets, and only partial descriptions of their facets are available.