Neighborly polytope
Encyclopedia
In geometry
and polyhedral combinatorics
, a k-neighborly polytope is a convex polytope
in which every set of k or fewer vertices forms a face. For instance, a 2-neighborly polytope is a polytope in which every pair of vertices
is connected by an edge
, forming a complete graph
. 2-neighborly polytopes with more than four vertices may exist only in spaces of four or more dimensions, and in general a k-neighborly polytope requires a dimension of 2k or more. A polytope is said to be neighborly, without specifying k, if it is k-neighborly for
, the maximum possible level of neighborliness for its dimension.
In a k-neighborly polytope with k ≥ 3, every 2-face must be a triangle, and in a k-neighborly polytope with k ≥ 4, every 3-face must be a tetrahedron. More generally, in any k-neighborly polytope, all faces of dimension less than k are simplices
.
The cyclic polytope
s formed as the convex hulls of finite sets of points on the moment curve (t, t2, ..., td) in d-dimensional space are automatically neighborly. Theodore Motzkin
conjectured that all neighborly polytopes are combinatorially equivalent to cyclic polytopes. However, contrary to this conjecture, there are many neighborly polytopes that are not cyclic: the number of combinatorially distinct neighborly polytopes grows superexponentially, both in the number of vertices of the polytope and in the dimension.
The convex hull
of a set of random points, drawn from a Gaussian distribution with the number of points proportional to the dimension, is with high probability k-neighborly for a value k that is also proportional to the dimension.
The number of faces of all dimensions of a neighborly polytope in an even number of dimensions is determined solely from its dimension and its number of vertices by the Dehn–Sommerville equations: the number of k-dimensional faces, fk, satisfies the inequality
where the asterisk means that the sums ends at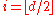
and final term of the sum should be halved if d is even. According to the upper bound theorem of , neighborly polytopes achieve the maximum possible number of faces of any n-vertex d-dimensional convex polytope.
A generalized version of the happy ending problem
applies to higher dimensional point sets, and imples that
for every dimension d and every n > d there exists a number m(d,n) with the property that every m points in general position
in d-dimensional space contain a subset of n points that form the vertices of a neighborly polytope.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and polyhedral combinatorics
Polyhedral combinatorics
Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher dimensional convex polytopes....
, a k-neighborly polytope is a convex polytope
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
in which every set of k or fewer vertices forms a face. For instance, a 2-neighborly polytope is a polytope in which every pair of vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
is connected by an edge
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
, forming a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
. 2-neighborly polytopes with more than four vertices may exist only in spaces of four or more dimensions, and in general a k-neighborly polytope requires a dimension of 2k or more. A polytope is said to be neighborly, without specifying k, if it is k-neighborly for
, the maximum possible level of neighborliness for its dimension.In a k-neighborly polytope with k ≥ 3, every 2-face must be a triangle, and in a k-neighborly polytope with k ≥ 4, every 3-face must be a tetrahedron. More generally, in any k-neighborly polytope, all faces of dimension less than k are simplices
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
.
The cyclic polytope
Cyclic polytope
In mathematics, a cyclic polytope, denoted C, is a convex polytope formed as a convex hull of n distinct points on a rational normal curve in Rd, where n is greater than d. These polytopes were studied by Constantin Carathéodory, David Gale, Theodore Motzkin, Victor Klee, and others...
s formed as the convex hulls of finite sets of points on the moment curve (t, t2, ..., td) in d-dimensional space are automatically neighborly. Theodore Motzkin
Theodore Motzkin
Theodore Samuel Motzkin was an Israeli-American mathematician.- Biography :Motzkin's father, Leo Motzkin, was a noted Russian Zionist leader.Motzkin received his Ph.D...
conjectured that all neighborly polytopes are combinatorially equivalent to cyclic polytopes. However, contrary to this conjecture, there are many neighborly polytopes that are not cyclic: the number of combinatorially distinct neighborly polytopes grows superexponentially, both in the number of vertices of the polytope and in the dimension.
The convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of a set of random points, drawn from a Gaussian distribution with the number of points proportional to the dimension, is with high probability k-neighborly for a value k that is also proportional to the dimension.
The number of faces of all dimensions of a neighborly polytope in an even number of dimensions is determined solely from its dimension and its number of vertices by the Dehn–Sommerville equations: the number of k-dimensional faces, fk, satisfies the inequality
where the asterisk means that the sums ends at
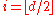and final term of the sum should be halved if d is even. According to the upper bound theorem of , neighborly polytopes achieve the maximum possible number of faces of any n-vertex d-dimensional convex polytope.A generalized version of the happy ending problem
Happy Ending problem
The Happy Ending problem is the following statement:This was one of the original results that led to the development of Ramsey theory....
applies to higher dimensional point sets, and imples that
for every dimension d and every n > d there exists a number m(d,n) with the property that every m points in general position
General position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
in d-dimensional space contain a subset of n points that form the vertices of a neighborly polytope.