Schläfli graph
Encyclopedia
In the mathematical
field of graph theory
, the Schläfli graph, named after Ludwig Schläfli
, is a 16-regular
undirected graph with 27 vertices and 216 edges. It is a strongly regular graph
with parameters srg(27, 16, 10, 8).
of the 27 lines on a cubic surface
is the complement
of the Schläfli graph. That is, two vertices are adjacent in the Schläfli graph if and only if the corresponding pair of lines are skew
.
The Schläfli graph may also be constructed from the system of eight-dimensional vectors,, and,
and the 24 other vectors obtained by permuting the first six coordinates of these three vectors.
These 27 vectors correspond to the vertices of the Schläfli graph; two vertices are adjacent if and only if the corresponding two vectors have 1 as their inner product.
to the complement graph
of the Clebsch graph
. Since the Clebsch graph is triangle-free
, the Schläfli graph is claw-free. It plays an important role in the structure theory for claw-free graphs by .
Any two skew lines of these 27 belong to a unique Schläfli double six configuration
, a set of 12 lines whose intersection graph is a crown graph
in which the two lines have disjoint neighborhoods. Correspondingly, in the Schläfli graph, each edge uv belongs uniquely to a subgraph in the form of a Cartesian product
of complete graph
s K6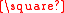
K2 in such a way that u and v belong to different K6 subgraphs of the product. The Schläfli graph has a total of 36 subgraphs of this form, one of which consists of the zero-one vectors in the eight-dimensional representation described above.
between two of its induced subgraphs of at most k vertices can be extended to an automorphism
of the whole graph. If a graph is 5-ultrahomogeneous, it is ultrahomogeneous for every k; the only finite connected graphs of this type are complete graph
s, Turán graph
s, 3 × 3 rook's graph
s, and the 5-cycle
. The infinite Rado graph
is countably ultrahomogeneous. There are only two connected graphs that are 4-ultrahomogeneous but not 5-ultrahomogeneous: the Schläfli graph and its complement. The proof relies on the classification of finite simple groups
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Schläfli graph, named after Ludwig Schläfli
Ludwig Schläfli
Ludwig Schläfli was a Swiss geometer and complex analyst who was one of the key figures in developing the notion of higher dimensional spaces. The concept of multidimensionality has since come to play a pivotal role in physics, and is a common element in science fiction...
, is a 16-regular
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
undirected graph with 27 vertices and 216 edges. It is a strongly regular graph
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
with parameters srg(27, 16, 10, 8).
Construction
The intersection graphIntersection graph
In the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...
of the 27 lines on a cubic surface
Cubic surface
A cubic surface is a projective variety studied in algebraic geometry. It is an algebraic surface in three-dimensional projective space defined by a single polynomial which is homogeneous of degree 3...
is the complement
Complement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
of the Schläfli graph. That is, two vertices are adjacent in the Schläfli graph if and only if the corresponding pair of lines are skew
Skew lines
In solid geometry, skew lines are two lines that do not intersect and are not parallel. Equivalently, they are lines that are not coplanar. A simple example of a pair of skew lines is the pair of lines through opposite edges of a regular tetrahedron...
.
The Schläfli graph may also be constructed from the system of eight-dimensional vectors,, and,
and the 24 other vectors obtained by permuting the first six coordinates of these three vectors.
These 27 vectors correspond to the vertices of the Schläfli graph; two vertices are adjacent if and only if the corresponding two vectors have 1 as their inner product.
Subgraphs and neighborhoods
The neighborhood of any vertex in the Schläfli graph forms a 16-vertex subgraph in which each vertex has 10 neighbors (the numbers 16 and 10 coming from the parameters of the Schläfli graph as a strongly regular graph). These subgraphs are all isomorphicGraph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
to the complement graph
Complement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
of the Clebsch graph
Clebsch graph
In the mathematical field of graph theory, the Clebsch graph is an undirected graph with 16 vertices and 40 edges. It is named after Alfred Clebsch, a German mathematician who discovered it in 1868...
. Since the Clebsch graph is triangle-free
Triangle-free graph
In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
, the Schläfli graph is claw-free. It plays an important role in the structure theory for claw-free graphs by .
Any two skew lines of these 27 belong to a unique Schläfli double six configuration
Configuration (geometry)
In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.Although certain specific...
, a set of 12 lines whose intersection graph is a crown graph
Crown graph
In graph theory, a branch of mathematics, a crown graph on 2n vertices is an undirected graph with two sets of vertices ui and vi and with an edge from ui to vj whenever i ≠ j...
in which the two lines have disjoint neighborhoods. Correspondingly, in the Schläfli graph, each edge uv belongs uniquely to a subgraph in the form of a Cartesian product
Cartesian product of graphs
In graph theory, the Cartesian product G \square H of graphs G and H is a graph such that* the vertex set of G \square H is the Cartesian product V × V; and...
of complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
s K6
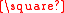K2 in such a way that u and v belong to different K6 subgraphs of the product. The Schläfli graph has a total of 36 subgraphs of this form, one of which consists of the zero-one vectors in the eight-dimensional representation described above.Ultrahomogeneity
A graph is defined to be k-ultrahomogeneous if every isomorphismGraph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
between two of its induced subgraphs of at most k vertices can be extended to an automorphism
Graph automorphism
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....
of the whole graph. If a graph is 5-ultrahomogeneous, it is ultrahomogeneous for every k; the only finite connected graphs of this type are complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
s, Turán graph
Turán graph
The Turán graph T is a graph formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and connecting two vertices by an edge whenever they belong to different subsets. The graph will have subsets of size \lceil n/r\rceil, and r- subsets of size \lfloor n/r\rfloor...
s, 3 × 3 rook's graph
Rook's graph
In graph theory, a rook's graph is a graph that represents all legal moves of the rook chess piece on a chessboard: each vertex represents a square on a chessboard and each edge represents a legal move...
s, and the 5-cycle
Cycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
. The infinite Rado graph
Rado graph
In the mathematical field of graph theory, the Rado graph, also known as the random graph or the Erdős–Renyi graph, is the unique countable graph R such that for any finite graph G and any vertex v of G, any embedding of G − v as an induced subgraph of R can be extended to an...
is countably ultrahomogeneous. There are only two connected graphs that are 4-ultrahomogeneous but not 5-ultrahomogeneous: the Schläfli graph and its complement. The proof relies on the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
.