Crown graph
Encyclopedia
In graph theory
, a branch of mathematics, a crown graph on 2n vertices is an undirected graph with two sets of vertices ui and vi and with an edge from ui to vj whenever i ≠ j. The crown graph can be viewed as a complete bipartite graph
from which the edges of a perfect matching have been removed, as the bipartite double cover
of a complete graph
, or as a bipartite Kneser graph
Hn,1 representing the 1-item and (n − 1)-item subsets of an n-item set, with an edge between two subsets whenever one is contained in the other.
, and the 8-vertex crown graph is isomorphic
to the graph of a cube
.
n(n − 1). Its achromatic number is n: one can find a complete coloring
by choosing each pair {ui, vi} as one of the color classes. Crown graphs are symmetric
and distance-transitive
. describe partitions of the edges of a crown graph into equal-length cycles.
The 2n-vertex crown graph may be embedded into four-dimensional Euclidean space in such a way that all of its edges have unit length. However, this embedding may also place some non-adjacent vertices a unit distance apart. An embedding in which edges are at unit distance and non-edges are not at unit distance requires at least n − 2 dimensions. This example shows that a graph may require very different dimensions to be represented as a unit distance graph
s and as a strict unit distance graph.
The minimum number of complete bipartite subgraphs
needed to cover the edges of a crown graph (its bipartite dimension
, or the size of a minimum biclique cover) is
the inverse function of the central binomial coefficient
.
The complement graph
of a 2n-vertex crown graph is the Cartesian product
of complete graph
s K2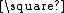
Kn, or equivalently the 2 × n rook's graph
.
, a traditional rule for arranging guests at a dinner table is that men and women should alternate positions, and that no married couple should sit next to each other. The arrangements satisfying this rule, for a party consisting of n married couples, can be described as the Hamiltonian cycles of a crown graph. For instance, the arrangements of vertices shown in the figure can be interpreted as seating charts of this type in which each husband and wife are seated as far apart as possible. The problem of counting the number of possible seating arrangements, or almost equivalently the number of Hamiltonian cycles in a crown graph, is known in combinatorics as the ménage problem
; for crown graphs with 6, 8, 10, ... vertices the number of (oriented) Hamiltonian cycles is
Crown graphs can be used to show that greedy coloring
algorithms behave badly in the worst case: if the vertices of a crown graph are presented to the algorithm in the order u0, v0, u1, v1, etc., then a greedy coloring uses n colors, whereas the optimal number of colors is two. This construction is attributed to ; crown graphs are sometimes called Johnson’s graphs with notation Jn . uses crown graphs as part of a construction showing hardness of approximation of coloring problems.
uses distances in crown graphs as an example of a metric space
that is difficult to embed into a normed vector space
.
As show, crown graphs are one of a small number of different types of graphs that can occur as distance-regular
circulant graph
s.
describe polygons that have crown graphs as their visibility graph
s; they use this example to show that representing visibility graphs as unions of complete bipartite graphs may not always be space-efficient.
A crown graph with 2n vertices, with its edges oriented from one side of the bipartition to the other, forms the standard example of a partially ordered set
with order dimension
n.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a branch of mathematics, a crown graph on 2n vertices is an undirected graph with two sets of vertices ui and vi and with an edge from ui to vj whenever i ≠ j. The crown graph can be viewed as a complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
from which the edges of a perfect matching have been removed, as the bipartite double cover
Bipartite double cover
In graph theoretic mathematics, the bipartite double cover of an undirected graph G is a bipartite covering graph of G, with twice as many vertices as G. It can be constructed as the tensor product of graphs G × K2...
of a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
, or as a bipartite Kneser graph
Kneser graph
In graph theory, the Kneser graph is the graph whose vertices correspond to the -element subsets of a set of elements, and where two vertices are connected if and only if the two corresponding sets are disjoint...
Hn,1 representing the 1-item and (n − 1)-item subsets of an n-item set, with an edge between two subsets whenever one is contained in the other.
Examples
The 6-vertex crown graph forms a cycleCycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
, and the 8-vertex crown graph is isomorphic
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
to the graph of a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
.
Properties
The number of edges in a crown graph is the pronic numberPronic number
A pronic number, oblong number, rectangular number or heteromecic number, is a number which is the product of two consecutive integers, that is, n . The n-th pronic number is twice the n-th triangular number and n more than the n-th square number...
n(n − 1). Its achromatic number is n: one can find a complete coloring
Complete coloring
In graph theory, complete coloring is the opposite of harmonious coloring in the sense that it is a vertex coloring in which every pair of colors appears on at least one pair of adjacent vertices. Equivalently, a complete coloring is minimal in the sense that it cannot be transformed into a proper...
by choosing each pair {ui, vi} as one of the color classes. Crown graphs are symmetric
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
and distance-transitive
Distance-transitive graph
In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices v and w at any distance i, and any other two vertices x and y at the same distance, there is an automorphism of the graph that carries v to x and w to y.A distance transitive...
. describe partitions of the edges of a crown graph into equal-length cycles.
The 2n-vertex crown graph may be embedded into four-dimensional Euclidean space in such a way that all of its edges have unit length. However, this embedding may also place some non-adjacent vertices a unit distance apart. An embedding in which edges are at unit distance and non-edges are not at unit distance requires at least n − 2 dimensions. This example shows that a graph may require very different dimensions to be represented as a unit distance graph
Unit distance graph
In mathematics, and particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points by an edge whenever the distance between the two points is exactly one...
s and as a strict unit distance graph.
The minimum number of complete bipartite subgraphs
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
needed to cover the edges of a crown graph (its bipartite dimension
Bipartite dimension
In the mathematical field of graph theory, the bipartite dimension of a graph G = is the minimum number of bicliques, that is, complete bipartite subgraphs, needed to cover all edges in E. A collection of bicliques covering all edges in G is called a biclique edge cover, or sometimes...
, or the size of a minimum biclique cover) is
the inverse function of the central binomial coefficient
Central binomial coefficient
In mathematics the nth central binomial coefficient is defined in terms of the binomial coefficient byThey are called central since they show up exactly in the middle of the even-numbered rows in Pascal's triangle...
.
The complement graph
Complement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
of a 2n-vertex crown graph is the Cartesian product
Cartesian product of graphs
In graph theory, the Cartesian product G \square H of graphs G and H is a graph such that* the vertex set of G \square H is the Cartesian product V × V; and...
of complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
s K2
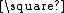Kn, or equivalently the 2 × n rook's graphRook's graph
In graph theory, a rook's graph is a graph that represents all legal moves of the rook chess piece on a chessboard: each vertex represents a square on a chessboard and each edge represents a legal move...
.
Applications
In etiquetteEtiquette
Etiquette is a code of behavior that delineates expectations for social behavior according to contemporary conventional norms within a society, social class, or group...
, a traditional rule for arranging guests at a dinner table is that men and women should alternate positions, and that no married couple should sit next to each other. The arrangements satisfying this rule, for a party consisting of n married couples, can be described as the Hamiltonian cycles of a crown graph. For instance, the arrangements of vertices shown in the figure can be interpreted as seating charts of this type in which each husband and wife are seated as far apart as possible. The problem of counting the number of possible seating arrangements, or almost equivalently the number of Hamiltonian cycles in a crown graph, is known in combinatorics as the ménage problem
Ménage problem
In combinatorial mathematics, the ménage problem or problème des ménages asks for the number of different ways in which it is possible to seat a set of heterosexual couples at a dining table so that men and women alternate and nobody sits next to his or her partner...
; for crown graphs with 6, 8, 10, ... vertices the number of (oriented) Hamiltonian cycles is
- 2, 12, 312, 9600, 416880, 23879520, 1749363840, ...
Crown graphs can be used to show that greedy coloring
Greedy coloring
In the study of graph coloring problems in mathematics and computer science, a greedy coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color...
algorithms behave badly in the worst case: if the vertices of a crown graph are presented to the algorithm in the order u0, v0, u1, v1, etc., then a greedy coloring uses n colors, whereas the optimal number of colors is two. This construction is attributed to ; crown graphs are sometimes called Johnson’s graphs with notation Jn . uses crown graphs as part of a construction showing hardness of approximation of coloring problems.
uses distances in crown graphs as an example of a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
that is difficult to embed into a normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
.
As show, crown graphs are one of a small number of different types of graphs that can occur as distance-regular
Distance-regular graph
In mathematics, a distance-regular graph is a regular graph such that for any two vertices v and w at distance i the number of vertices adjacent to w and at distance j from v is the same. Every distance-transitive graph is distance-regular...
circulant graph
Circulant graph
In graph theory, a circulant graph is an undirected graph that has a cyclic group of symmetries that includes a symmetry taking any vertex to any other vertex.-Equivalent definitions:Circulant graphs can be described in several equivalent ways:...
s.
describe polygons that have crown graphs as their visibility graph
Visibility graph
In computational geometry and robot motion planning, a visibility graph is a graph of intervisible locations, typically for a set of points and obstacles in the Euclidean plane. Each node in the graph represents a point location, and each edge represents a visible connection between them...
s; they use this example to show that representing visibility graphs as unions of complete bipartite graphs may not always be space-efficient.
A crown graph with 2n vertices, with its edges oriented from one side of the bipartition to the other, forms the standard example of a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
with order dimension
Order dimension
In mathematics, the dimension of a partially ordered set is the smallest number of total orders the intersection of which gives rise to the partial order....
n.