In graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

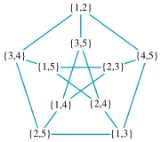
, the Kneser graph is the graph whose vertices correspond to the -element subsets of a set of elements, and where two vertices are connected if and only if the two corresponding sets are disjoint. Kneser graphs are named after Martin Kneser

Martin Kneser

Martin Kneser was a German mathematician. His father Hellmuth Kneser and grandfather Adolf Kneser were also mathematicians....

, who first investigated them in 1955.
The complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

 on vertices is the Kneser graph .

The Kneser graph is known as the odd graph

Odd graph

In the mathematical field of graph theory, the odd graphs On are a family of symmetric graphs with high odd girth, defined from certain set systems. They include and generalize the Petersen graph.-Definition and examples:...

 ; the odd graph is isomorphic to the Petersen Graph

Petersen graph

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...

.

• The Kneser graph is vertex transitive
  Vertex-transitive graph
  In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
  
   and edge transitive
  Edge-transitive graph
  In the mathematical field of graph theory, an edge-transitive graph is a graph G such that, given any two edges e1 and e2 of G, there is anautomorphism of G that maps e1 to e2....
  
  .