
Forbidden graph characterization
Encyclopedia
A forbidden graph characterization is a method of specifying
a family of graph
, or hypergraph
, structures.
Families vary in the nature of what is forbidden. In general, a structure G is a member of a family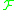 if and only if
if and only if
a forbidden substructure is not contained in G. The forbidden substructure might simply be a subgraph, or a substructure from which one might derive (via, e.g., edge contraction
or subdivision) that which is forbidden. Thus, the forbidden structure might be one of:
(Such forbidden structures can also be called obstruction sets.)
Forbidden graph characterizations are utilized in combinatorial algorithms, often for identifying a structure. Such methods can provide a polynomial-time algorithm for determining a graph's membership in a specific family (i.e., a polynomial-time implementation of an indicator function).
A well-known characterization of this kind is the Kuratowski theorem that provides two forbidden homeomorphic subgraphs, using which, one may determine a graph's planarity
. Another is the Robertson–Seymour theorem
that proves the existence of a forbidden minor characterization for several graph families.
Characterization (mathematics)
In mathematics, the statement that "Property P characterizes object X" means, not simply that X has property P, but that X is the only thing that has property P. It is also common to find statements such as "Property Q characterises Y up to isomorphism". The first type of statement says in...
a family of graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, or hypergraph
Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
, structures.
Families vary in the nature of what is forbidden. In general, a structure G is a member of a family
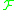 if and only if
if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
a forbidden substructure is not contained in G. The forbidden substructure might simply be a subgraph, or a substructure from which one might derive (via, e.g., edge contraction
Edge contraction
In graph theory, an edge contraction is an operation which removes an edge from a graph while simultaneously merging together the two vertices it previously connected. Edge contraction is a fundamental operation in the theory of graph minors...
or subdivision) that which is forbidden. Thus, the forbidden structure might be one of:
- subgraphs,
- graph minors,
- homeomorphicHomeomorphism (graph theory)In graph theory, two graphs G and G' are homeomorphic if there is an isomorphism from some subdivision of G to some subdivision of G'...
subgraphs (also called topological minors).
(Such forbidden structures can also be called obstruction sets.)
Forbidden graph characterizations are utilized in combinatorial algorithms, often for identifying a structure. Such methods can provide a polynomial-time algorithm for determining a graph's membership in a specific family (i.e., a polynomial-time implementation of an indicator function).
A well-known characterization of this kind is the Kuratowski theorem that provides two forbidden homeomorphic subgraphs, using which, one may determine a graph's planarity
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
. Another is the Robertson–Seymour theorem
Robertson–Seymour theorem
In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering...
that proves the existence of a forbidden minor characterization for several graph families.
List of forbidden characterizations for graphs and hypergraphs
| Family | Forbidden graphs | Relation | Reference | |
|---|---|---|---|---|
| Forests | loops, pairs of parallel edges, and cycles Cycle (graph theory) In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,... of all lengths |
subgraph | Definition | |
| a loop (for multigraphs) or a triangle K3 (for simple graphs) | graph minor | Definition | ||
| Claw-free graphs | star Star (graph theory) In graph theory, a star Sk is the complete bipartite graph K1,k: a tree with one internal node and k leaves... K1,3 |
induced subgraph | Definition | |
| Comparability graph Comparability graph In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order... s |
induced subgraph | |||
| Triangle-free graph Triangle-free graph In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally... s |
triangle K3 | induced subgraph | Definition | |
| Planar graph Planar graph In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints... s |
K5 and K3,3 | homeomorphic subgraph | Kuratowski theorem | |
| K5 and K3,3 | graph minor | Wagner's theorem | ||
| Outerplanar graph Outerplanar graph In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges... s |
K4 and K2,3 | graph minor | , p. 107 | |
| Graphs of fixed genus | a finite obstruction set | graph minor | , p. 275 | |
| Apex graph Apex graph In graph theory, a branch of mathematics, an apex graph is a graph that can be made planar by the removal of a single vertex. The deleted vertex is called an apex of the graph. We say an apex, not the apex because an apex graph may have more than one apex... s |
a finite obstruction set | graph minor | ||
| Linklessly embeddable graphs Linkless embedding In topological graph theory, a mathematical discipline, a linkless embedding of an undirected graph is an embedding of the graph into Euclidean space in such a way that no two cycles of the graph have nonzero linking number. A flat embedding is an embedding with the property that every cycle is the... |
The Petersen family Petersen family In graph theory, the Petersen family is a set of seven undirected graphs that includes the Petersen graph and the complete graph K6. The Petersen family is named after Danish mathematician Julius Petersen, the namesake of the Petersen graph.... |
graph minor | ||
| Bipartite graph Bipartite graph In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets... s |
odd cycles | subgraph | ||
| Chordal graph Chordal graph In the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes... s |
cycles of length 4 or more | induced subgraph | ||
| Perfect graph Perfect graph In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph.... s |
cycles of odd length 5 or more or their complements Complement graph In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and... |
induced subgraph | ||
| Line graph of graph Line graph In graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G... s |
nine forbidden subgraphs (listed here) | induced subgraph | ||
| Graph unions of cactus graph Cactus graph In graph theory, a cactus is a connected graph in which any two simple cycles have at most one vertex in common. Equivalently, every edge in such a graph belongs to at most one simple cycle. Equivalently, every block is an edge or a cycle.-Properties:Cacti are outerplanar graphs... s |
the four-vertex diamond graph Diamond graph In the mathematical field of graph theory, the diamond graph is a planar undirected graph with 4 vertices and 5 edges. It consists of a complete graph K_4 minus one edge.... formed by removing an edge from the complete graph Complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:... K4 |
graph minor | ||
| Ladder graph Ladder graph In the mathematical field of graph theory, the ladder graph Ln is a planar undirected graph with 2n vertices and n+2 edges.... s |
K2,3 and its dual graph Dual graph In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual... |
homeomorphic subgraph | ||
| Helly circular-arc graphs | induced subgraph | |||
| split graph Split graph In graph theory, a branch of mathematics, a split graph is a graph in which the vertices can be partitioned into a clique and an independent set... s |
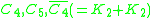 |
induced subgraph | ||
| treewidth ≤ 2 (branchwidth ≤ 2) | K4 | graph minor | , p. 327 | |
| treewidth ≤ 3 | K5, octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... , pentagonal prism Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... , Wagner graph Wagner graph In the mathematical field of graph theory, the Wagner graph is a 3-regular graph with 8 vertices and 12 edges. It is the 8-vertex Möbius ladder graph.-Properties:... |
graph minor | ||
| branchwidth ≤ 3 | K5, octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... , cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... , Wagner graph Wagner graph In the mathematical field of graph theory, the Wagner graph is a 3-regular graph with 8 vertices and 12 edges. It is the 8-vertex Möbius ladder graph.-Properties:... |
graph minor | ||
| Complement-reducible graphs (cographs) Cograph In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union... |
4-vertex path P4 | induced subgraph | ||
| Trivially perfect graphs | 4-vertex path P4 and 4-vertex cycle C4 | induced subgraph | ||
| Threshold graph Threshold graph In graph theory, a threshold graph is a graph that can be constructed from a one-vertex graph by repeated applications of the following two operations:#Addition of a single isolated vertex to the graph.... s |
4-vertex path P4, 4-vertex cycle C4, and complement of C4 | induced subgraph | ||
| Line graph of 3-uniform linear hypergraphs | a finite list of forbidden induced subgraphs with minimum degree at least 19 | induced subgraph | ||
| Line graph of k-uniform linear hypergraphs, k > 3 | a finite list of forbidden induced subgraphs with minimum edge degree at least 2k2 − 3k + 1 | induced subgraph | ||
| General theorems | ||||
| a family defined by an induced-hereditary property | a (not necessarily finite) obstruction set | induced subgraph | ||
| a family defined by an minor-hereditary property | a finite obstruction set | graph minor | Robertson–Seymour theorem Robertson–Seymour theorem In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering... |

