
Ladder graph
Encyclopedia
In the mathematical
field of graph theory
, the ladder graph Ln is a planar
undirected graph with 2n vertices and n+2(n-1) edges.
The ladder graph can be obtained as the Cartesian product
of two path graph
s, one of which has only one edge: Ln,1 = Pn × P1. Adding two more crossed edges connecting the four degree-two vertices of a ladder graph produces a cubic graph
, the Möbius ladder
.
By construction, the ladder graph Ln is isomorphic to the grid graph G2,n and looks like a ladder with n rungs. It is Hamiltonian with girth 4 (if n>1) and chromatic index 3 (if n>2).
The chromatic number of the ladder graph is 2 and its chromatic polynomial
is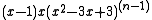 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the ladder graph Ln is a planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
undirected graph with 2n vertices and n+2(n-1) edges.
The ladder graph can be obtained as the Cartesian product
Cartesian product of graphs
In graph theory, the Cartesian product G \square H of graphs G and H is a graph such that* the vertex set of G \square H is the Cartesian product V × V; and...
of two path graph
Path graph
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
s, one of which has only one edge: Ln,1 = Pn × P1. Adding two more crossed edges connecting the four degree-two vertices of a ladder graph produces a cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
, the Möbius ladder
Möbius ladder
In graph theory, the Möbius ladder Mn is a cubic circulant graph with an even number n of vertices, formed from an n-cycle by adding edges connecting opposite pairs of vertices in the cycle...
.
By construction, the ladder graph Ln is isomorphic to the grid graph G2,n and looks like a ladder with n rungs. It is Hamiltonian with girth 4 (if n>1) and chromatic index 3 (if n>2).
The chromatic number of the ladder graph is 2 and its chromatic polynomial
Chromatic polynomial
The chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...
is
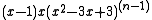 .
.
