
Apex graph
Encyclopedia
In graph theory
, a branch of mathematics, an apex graph is a graph that can be made planar
by the removal of a single vertex. The deleted vertex is called an apex of the graph. We say an apex, not the apex because an apex graph may have more than one apex (for example, in the minimal nonplanar graphs K5 or K3,3, every vertex is an apex). This class includes graphs that are themselves planar, in which case again every vertex is an apex. For technical reasons, it also includes the null graph
.
Apex graphs are closed
under the operation of taking minors
and play a role in several other aspects of graph minor theory: linkless embedding
, Hadwiger's conjecture
, YΔY-reducible graphs, and relations between treewidth and graph diameter
.
under the operation of taking minors
: contracting any edge, or removing any edge or vertex, leads to another apex graph. For, if G is an apex graph with apex v, then any contraction or removal that does not involve v preserves the planarity of the remaining graph, as does any edge removal of an edge incident to v. If an edge incident to v is contracted, the effect on the remaining graph is equivalent to the removal of the other endpoint of the edge. And if v itself is removed, any other vertex may be chosen as the apex.
Because they form a minor-closed family of graphs
, the apex graphs have a forbidden graph characterization: there exists a finite set A of minor-minimal non-apex graphs such that a graph is an apex graph if and only if it does not contain as a minor any graph in A. However, a complete description of the graphs in A remains unknown.
Despite the unknown set of forbidden minors, it is possible to test whether a given graph is an apex graph, and if so, to find an apex for the graph, in linear time. More generally, for any fixed constant k, it is possible to recognize in linear time the k-apex graphs, the graphs in which the removal of some carefully chosen set of at most k vertices leads to a planar graph. If k is variable, however, the problem is NP-complete
.
, and the remaining vertex needs at most one additional color. used this fact in their proof of the case k = 6 of the Hadwiger conjecture
, the statement that every 6-chromatic graph has the complete graph
K6 as a minor: they showed that any minimal counterexample to the conjecture would have to be an apex graph, but since there are no 6-chromatic apex graphs such a counterexample cannot exist.
conjectured that every 6-vertex-connected graph that does not have K6 as a minor must be an apex graph. If this were proved, the Robertson–Seymour–Thomas result on the Hadwiger conjecture would be an immediate consequence.
and treewidth: there exists a function ƒ such that the treewidth of a diameter-d graph in F is at most ƒ(d). The apex graphs do not have bounded local treewidth: the apex graphs formed by connecting an apex vertex to every vertex of an n × n grid graph have treewidth n and diameter 2, so the treewidth is not bounded by a function of diameter for these graphs. However, apex graphs are intimately connected to bounded local treewidth: the minor-closed graph families F that have bounded local treewidth are exactly the families that have an apex graph as one of their forbidden minors. A minor-closed family of graphs that has an apex graph as one of its forbidden minors is known as apex-minor-free. With this terminology, the connection between apex graphs and local treewidth can be restated as the fact that apex-minor-free graph families are the same as minor-closed graph families with bounded local treewidth.
The concept of bounded local treewidth forms the basis of the theory of bidimensionality
, and allows for many algorithmic problems on apex-minor-free graphs to be solved exactly by a polynomial-time algorithm or a fixed-parameter tractable algorithm, or approximated using a polynomial time approximation scheme. Apex-minor-free graph families obey a strengthened version of the graph structure theorem
, leading to additional approximation algorithms for graph coloring
and the travelling salesman problem
. However, some of these results can also be extended to arbitrary minor-closed graph families via structure theorems relating them to apex-minor-free graphs.
τ − 1: simply add that number of bridges to the planar embedding, connecting together all the faces into which v must be connected. For instance, adding a single vertex to an outerplanar graph
(a graph with τ = 1) produces a planar graph. When G\{v} is 3-connected, his bound is within a constant factor of optimal: every surface embedding of G requires genus at least τ/160. However, it is NP-hard
to determine the optimal genus of a surface embedding of an apex graph.
By using SPQR trees to encode the possible embeddings of the planar part of an apex graph, it is possible to compute a drawing
of the graph in the plane in which the only crossings involve the apex vertex, minimizing the total number of crossings, in polynomial time. However, if arbitrary crossings are allowed, it becomes NP-hard to minimize the number of crossings, even in the special case of apex graphs formed by adding a single edge to a planar graph.
Apex graphs are also linklessly embeddable
in three-dimensional space: they can be embedded in such a way that each cycle in the graph is the boundary of a disk that is not crossed by any other feature of the graph. A drawing of this type may be obtained by drawing the planar part of the graph in a plane, placing the apex above the plane, and connecting the apex by straight-line edges to each of its neighbors. Linklessly embeddable graphs form a minor-closed family with the seven graphs in the Petersen family
as their minimal forbidden minors; therefore, these graphs are also forbidden as minors for the apex graphs. However, there exist linklessly embeddable graphs that are not apex graphs.
Like the apex graphs and the linkless embeddable graphs, the YΔY-reducible graphs are closed under graph minors. And, like the linkless embeddable graphs, the YΔY-reducible graphs have the seven graphs in the Petersen family
as forbidden minors, prompting the question of whether these are the only forbidden minors and whether the YΔY-reducible graphs are the same as the linkless embeddable graphs. However, Neil Robertson provided an example of an apex graph that is not YΔY-reducible. Since every apex graph is linkless embeddable, this shows that there are graphs that are linkless embeddable but not YΔY-reducible and therefore that there are additional forbidden minors for the YΔY-reducible graphs.
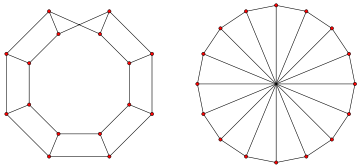
Robertson's apex graph is shown in the figure. It can be obtained by connecting an apex vertex to each of the degree-three vertices of a rhombic dodecahedron
, or by merging together two diametrally opposed vertices of a four-dimensional hypercube graph. Because the rhombic dodecahedron's graph is planar, Robertson's graph is an apex graph. It is a triangle-free graph
with minimum degree
four, so it cannot be changed by any YΔY-reduction.
 If a graph is an apex graph, it is not necessarily the case that it has a unique apex. For instance, in the minor-minimal nonplanar graphs K5 and K3,3, any of the vertices can be chosen as the apex. defined a nearly planar graph to be a nonplanar apex graph with the property that all vertices can be the apex of the graph; thus, K5 and K3,3 are nearly planar. He provided a classification of these graphs into four subsets, one of which consists of the graphs that (like the Möbius ladder
If a graph is an apex graph, it is not necessarily the case that it has a unique apex. For instance, in the minor-minimal nonplanar graphs K5 and K3,3, any of the vertices can be chosen as the apex. defined a nearly planar graph to be a nonplanar apex graph with the property that all vertices can be the apex of the graph; thus, K5 and K3,3 are nearly planar. He provided a classification of these graphs into four subsets, one of which consists of the graphs that (like the Möbius ladder
s) can be embedded onto the Möbius strip
in such a way that the single edge of the strip coincides with a Hamiltonian cycle of the graph. Prior to the proof of the four color theorem
, he proved that every nearly planar graph can be colored with at most four colors, except for the graphs formed from a wheel graph
with an odd outer cycle by replacing the hub vertex with two adjacent vertices, which require five colors. Additionally, he proved that, with a single exception (the eight-vertex complement graph
of the cube
) every nearly planar graph has an embedding onto the projective plane
.
However, the phrase "nearly planar graph" is highly ambiguous: it has also been used to refer to apex graphs, graphs formed by adding one edge to a planar graph, and graphs formed from a planar embedded graph by replacing a bounded number of faces by "vortexes" of bounded pathwidth, as well as for other less precisely-defined sets of graphs.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a branch of mathematics, an apex graph is a graph that can be made planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
by the removal of a single vertex. The deleted vertex is called an apex of the graph. We say an apex, not the apex because an apex graph may have more than one apex (for example, in the minimal nonplanar graphs K5 or K3,3, every vertex is an apex). This class includes graphs that are themselves planar, in which case again every vertex is an apex. For technical reasons, it also includes the null graph
Null graph
In the mathematical field of graph theory, the null graph may refer either to the order zero graph, or alternatively, to any edgeless graph .-Order zero graph:...
.
Apex graphs are closed
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under the operation of taking minors
Minor (graph theory)
In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....
and play a role in several other aspects of graph minor theory: linkless embedding
Linkless embedding
In topological graph theory, a mathematical discipline, a linkless embedding of an undirected graph is an embedding of the graph into Euclidean space in such a way that no two cycles of the graph have nonzero linking number. A flat embedding is an embedding with the property that every cycle is the...
, Hadwiger's conjecture
Hadwiger conjecture (graph theory)
In graph theory, the Hadwiger conjecture states that, if all proper colorings of an undirected graph G use k or more colors, then one can find k disjoint connected subgraphs of G such that each subgraph is connected by an edge to each other subgraph...
, YΔY-reducible graphs, and relations between treewidth and graph diameter
Distance (graph theory)
In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance...
.
Characterization and recognition
Apex graphs are closedClosure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under the operation of taking minors
Minor (graph theory)
In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....
: contracting any edge, or removing any edge or vertex, leads to another apex graph. For, if G is an apex graph with apex v, then any contraction or removal that does not involve v preserves the planarity of the remaining graph, as does any edge removal of an edge incident to v. If an edge incident to v is contracted, the effect on the remaining graph is equivalent to the removal of the other endpoint of the edge. And if v itself is removed, any other vertex may be chosen as the apex.
Because they form a minor-closed family of graphs
Robertson–Seymour theorem
In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering...
, the apex graphs have a forbidden graph characterization: there exists a finite set A of minor-minimal non-apex graphs such that a graph is an apex graph if and only if it does not contain as a minor any graph in A. However, a complete description of the graphs in A remains unknown.
Despite the unknown set of forbidden minors, it is possible to test whether a given graph is an apex graph, and if so, to find an apex for the graph, in linear time. More generally, for any fixed constant k, it is possible to recognize in linear time the k-apex graphs, the graphs in which the removal of some carefully chosen set of at most k vertices leads to a planar graph. If k is variable, however, the problem is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
.
Chromatic number
Every apex graph has chromatic number at most five: the underlying planar graph requires at most four colors by the four color theoremFour color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
, and the remaining vertex needs at most one additional color. used this fact in their proof of the case k = 6 of the Hadwiger conjecture
Hadwiger conjecture (graph theory)
In graph theory, the Hadwiger conjecture states that, if all proper colorings of an undirected graph G use k or more colors, then one can find k disjoint connected subgraphs of G such that each subgraph is connected by an edge to each other subgraph...
, the statement that every 6-chromatic graph has the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
K6 as a minor: they showed that any minimal counterexample to the conjecture would have to be an apex graph, but since there are no 6-chromatic apex graphs such a counterexample cannot exist.
conjectured that every 6-vertex-connected graph that does not have K6 as a minor must be an apex graph. If this were proved, the Robertson–Seymour–Thomas result on the Hadwiger conjecture would be an immediate consequence.
Local treewidth
A graph family F has bounded local treewidth if the graphs in F obey a functional relationship between diameterDistance (graph theory)
In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance...
and treewidth: there exists a function ƒ such that the treewidth of a diameter-d graph in F is at most ƒ(d). The apex graphs do not have bounded local treewidth: the apex graphs formed by connecting an apex vertex to every vertex of an n × n grid graph have treewidth n and diameter 2, so the treewidth is not bounded by a function of diameter for these graphs. However, apex graphs are intimately connected to bounded local treewidth: the minor-closed graph families F that have bounded local treewidth are exactly the families that have an apex graph as one of their forbidden minors. A minor-closed family of graphs that has an apex graph as one of its forbidden minors is known as apex-minor-free. With this terminology, the connection between apex graphs and local treewidth can be restated as the fact that apex-minor-free graph families are the same as minor-closed graph families with bounded local treewidth.
The concept of bounded local treewidth forms the basis of the theory of bidimensionality
Bidimensionality
Bidimensionality theory characterizes a broad range of graph problems that admit efficient approximate, fixed-parameter or kernel solutions in a broad range of graphs. These graph classes include planar graphs, map graphs, bounded-genus graphs and graphs excluding any fixed minor...
, and allows for many algorithmic problems on apex-minor-free graphs to be solved exactly by a polynomial-time algorithm or a fixed-parameter tractable algorithm, or approximated using a polynomial time approximation scheme. Apex-minor-free graph families obey a strengthened version of the graph structure theorem
Graph structure theorem
In mathematics, the graph structure theorem is a major result in the area of graph theory. The result establishes a deep and fundamental connection between the theory of graph minors and topological embeddings. The theorem is stated in the seventeenth of a series of 23 papers by Neil Robertson and...
, leading to additional approximation algorithms for graph coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
and the travelling salesman problem
Travelling salesman problem
The travelling salesman problem is an NP-hard problem in combinatorial optimization studied in operations research and theoretical computer science. Given a list of cities and their pairwise distances, the task is to find the shortest possible tour that visits each city exactly once...
. However, some of these results can also be extended to arbitrary minor-closed graph families via structure theorems relating them to apex-minor-free graphs.
Embeddings
If G is an apex graph with apex v, and τ is the minimum number of faces needed to cover all the neighbors of v in a planar embedding of G\{v}, then G may be embedded onto a two-dimensional surface of genusGenus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
τ − 1: simply add that number of bridges to the planar embedding, connecting together all the faces into which v must be connected. For instance, adding a single vertex to an outerplanar graph
Outerplanar graph
In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...
(a graph with τ = 1) produces a planar graph. When G\{v} is 3-connected, his bound is within a constant factor of optimal: every surface embedding of G requires genus at least τ/160. However, it is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
to determine the optimal genus of a surface embedding of an apex graph.
By using SPQR trees to encode the possible embeddings of the planar part of an apex graph, it is possible to compute a drawing
Graph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
of the graph in the plane in which the only crossings involve the apex vertex, minimizing the total number of crossings, in polynomial time. However, if arbitrary crossings are allowed, it becomes NP-hard to minimize the number of crossings, even in the special case of apex graphs formed by adding a single edge to a planar graph.
Apex graphs are also linklessly embeddable
Linkless embedding
In topological graph theory, a mathematical discipline, a linkless embedding of an undirected graph is an embedding of the graph into Euclidean space in such a way that no two cycles of the graph have nonzero linking number. A flat embedding is an embedding with the property that every cycle is the...
in three-dimensional space: they can be embedded in such a way that each cycle in the graph is the boundary of a disk that is not crossed by any other feature of the graph. A drawing of this type may be obtained by drawing the planar part of the graph in a plane, placing the apex above the plane, and connecting the apex by straight-line edges to each of its neighbors. Linklessly embeddable graphs form a minor-closed family with the seven graphs in the Petersen family
Petersen family
In graph theory, the Petersen family is a set of seven undirected graphs that includes the Petersen graph and the complete graph K6. The Petersen family is named after Danish mathematician Julius Petersen, the namesake of the Petersen graph....
as their minimal forbidden minors; therefore, these graphs are also forbidden as minors for the apex graphs. However, there exist linklessly embeddable graphs that are not apex graphs.
YΔY-reducibility
A connected graph is YΔY-reducible if it can be reduced to a single vertex by a sequence of steps, each of which is a Δ-Y or Y-Δ transform, the removal of a self-loop or multiple adjacency, the removal of a vertex with one neighbor, and the replacement of a vertex of degree two and its two neighboring edges by a single edge.Like the apex graphs and the linkless embeddable graphs, the YΔY-reducible graphs are closed under graph minors. And, like the linkless embeddable graphs, the YΔY-reducible graphs have the seven graphs in the Petersen family
Petersen family
In graph theory, the Petersen family is a set of seven undirected graphs that includes the Petersen graph and the complete graph K6. The Petersen family is named after Danish mathematician Julius Petersen, the namesake of the Petersen graph....
as forbidden minors, prompting the question of whether these are the only forbidden minors and whether the YΔY-reducible graphs are the same as the linkless embeddable graphs. However, Neil Robertson provided an example of an apex graph that is not YΔY-reducible. Since every apex graph is linkless embeddable, this shows that there are graphs that are linkless embeddable but not YΔY-reducible and therefore that there are additional forbidden minors for the YΔY-reducible graphs.
Robertson's apex graph is shown in the figure. It can be obtained by connecting an apex vertex to each of the degree-three vertices of a rhombic dodecahedron
Rhombic dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
, or by merging together two diametrally opposed vertices of a four-dimensional hypercube graph. Because the rhombic dodecahedron's graph is planar, Robertson's graph is an apex graph. It is a triangle-free graph
Triangle-free graph
In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
with minimum degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
four, so it cannot be changed by any YΔY-reduction.
Nearly planar graphs

Möbius ladder
In graph theory, the Möbius ladder Mn is a cubic circulant graph with an even number n of vertices, formed from an n-cycle by adding edges connecting opposite pairs of vertices in the cycle...
s) can be embedded onto the Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
in such a way that the single edge of the strip coincides with a Hamiltonian cycle of the graph. Prior to the proof of the four color theorem
Four color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
, he proved that every nearly planar graph can be colored with at most four colors, except for the graphs formed from a wheel graph
Wheel graph
In the mathematical discipline of graph theory, a wheel graph Wn is a graph with n vertices, formed by connecting a single vertex to all vertices of an -cycle. The numerical notation for wheels is used inconsistently in the literature: some authors instead use n to refer to the length of the cycle,...
with an odd outer cycle by replacing the hub vertex with two adjacent vertices, which require five colors. Additionally, he proved that, with a single exception (the eight-vertex complement graph
Complement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
of the cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
) every nearly planar graph has an embedding onto the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
.
However, the phrase "nearly planar graph" is highly ambiguous: it has also been used to refer to apex graphs, graphs formed by adding one edge to a planar graph, and graphs formed from a planar embedded graph by replacing a bounded number of faces by "vortexes" of bounded pathwidth, as well as for other less precisely-defined sets of graphs.

