
Wheel graph
Encyclopedia
In the mathematical discipline of graph theory
, a wheel graph Wn is a graph with n vertices, formed by connecting a single vertex to all vertices of an (n-1)-cycle
. The numerical notation for wheels is used inconsistently in the literature: some authors instead use n to refer to the length of the cycle, so that their Wn is the graph we denote Wn+1. A wheel graph can also be defined as the 1-skeleton of an (n-1)-gonal pyramid
.
Wheel graphs are planar graph
s, and as such have a unique planar embedding. More specifically, every wheel graph is a Halin graph
. They are self-dual: the planar dual
of any wheel graph is an isomorphic graph. Any maximal planar graph, other than K4 = W4, contains as a subgraph either W5 or W6.
There is always a Hamiltonian cycle in the wheel graph and there are cycles in Wn .
cycles in Wn .
For odd values of n, Wn is a perfect graph
with chromatic number 3: the vertices of the cycle can be given two colors, and the center vertex given a third color. For even n, Wn has chromatic number 4, and (when n ≥ 6) is not perfect. W7 is the only wheel graph that is a unit distance graph
in the Euclidean plane.
The chromatic polynomial
of the wheel graph Wn is :

In matroid
theory, two particularly important special classes of matroids are the wheel matroids and the whirl matroids, both derived from wheel graphs. The k-wheel matroid is the cycle matroid of a wheel Wk+1, while the k-whirl matroid is derived from the k-wheel by considering the outer cycle of the wheel, as well as all of its spanning tree
s, to be independent.
The wheel W6 supplied a counterexample to a conjecture of Paul Erdős
on Ramsey theory
: he had conjectured that the complete graph has the smallest Ramsey number among all graphs with the same chromatic number, but Faudree and McKay (1993) showed W6 has Ramsey number 17 while the complete graph with the same chromatic number, K4, has Ramsey number 18. That is, for every 17-vertex graph G, either G or its complement contains W6 as a subgraph, while neither the 17-vertex Paley graph
nor its complement contains a copy of K4.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a wheel graph Wn is a graph with n vertices, formed by connecting a single vertex to all vertices of an (n-1)-cycle
Cycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
. The numerical notation for wheels is used inconsistently in the literature: some authors instead use n to refer to the length of the cycle, so that their Wn is the graph we denote Wn+1. A wheel graph can also be defined as the 1-skeleton of an (n-1)-gonal pyramid
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
.
Wheel graphs are planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s, and as such have a unique planar embedding. More specifically, every wheel graph is a Halin graph
Halin graph
In graph theory, a mathematical discipline, a Halin graph is a planar graph constructed from a plane embedding of a tree with at least four vertices and with no vertices of degree 2, by connecting all the leaves of the tree with a cycle that passes around the tree in the natural cyclic order...
. They are self-dual: the planar dual
Dual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
of any wheel graph is an isomorphic graph. Any maximal planar graph, other than K4 = W4, contains as a subgraph either W5 or W6.
There is always a Hamiltonian cycle in the wheel graph and there are
 cycles in Wn .
cycles in Wn .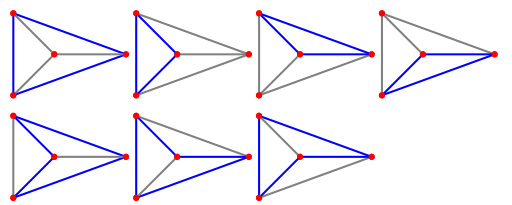 The 7 cycles of the wheel graph W4. |
For odd values of n, Wn is a perfect graph
Perfect graph
In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....
with chromatic number 3: the vertices of the cycle can be given two colors, and the center vertex given a third color. For even n, Wn has chromatic number 4, and (when n ≥ 6) is not perfect. W7 is the only wheel graph that is a unit distance graph
Unit distance graph
In mathematics, and particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points by an edge whenever the distance between the two points is exactly one...
in the Euclidean plane.
The chromatic polynomial
Chromatic polynomial
The chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...
of the wheel graph Wn is :

In matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
theory, two particularly important special classes of matroids are the wheel matroids and the whirl matroids, both derived from wheel graphs. The k-wheel matroid is the cycle matroid of a wheel Wk+1, while the k-whirl matroid is derived from the k-wheel by considering the outer cycle of the wheel, as well as all of its spanning tree
Spanning tree
Spanning tree can refer to:* Spanning tree , a tree which contains every vertex of a more general graph* Spanning tree protocol, a protocol for finding spanning trees in bridged networks...
s, to be independent.
The wheel W6 supplied a counterexample to a conjecture of Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
on Ramsey theory
Ramsey theory
Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of mathematics that studies the conditions under which order must appear...
: he had conjectured that the complete graph has the smallest Ramsey number among all graphs with the same chromatic number, but Faudree and McKay (1993) showed W6 has Ramsey number 17 while the complete graph with the same chromatic number, K4, has Ramsey number 18. That is, for every 17-vertex graph G, either G or its complement contains W6 as a subgraph, while neither the 17-vertex Paley graph
Paley graph
In mathematics, and specifically graph theory, Paley graphs, named after Raymond Paley, are dense undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ in a quadratic residue. The Paley graphs form an infinite family of conference...
nor its complement contains a copy of K4.

