In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the dual graph of a given planar graph

Planar graph

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...

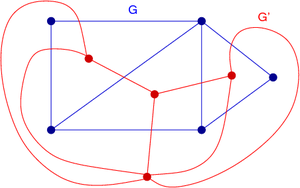
 G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding

Graph embedding

In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...

 of G. The term "dual

Duality (mathematics)

In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...

" is used because this property is symmetric

Symmetric function

In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...

, meaning that if H is a dual of G, then G is a dual of H (if G is connected). The same notion of duality may also be used for more general embeddings of graphs on manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

s.

Properties

• The dual of a planar graph
  Planar graph
  In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
  
   is a planar multigraph
  Multigraph
  In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....
  
   - multiple edges.
• If G is a connected graph and if G′ is a dual of G then G is a dual of G′.

• Dual graphs are not unique, in the sense that the same graph can have non-isomorphic
  Graph isomorphism
  In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
  
   dual graphs because the dual graph depends on a particular plane embedding. In the picture, red graphs are not isomorphic because the upper one has a vertex with degree 6 (the outer region).

Because of the dualism, any result involving counting regions and vertices can be dualized by exchanging them.

Algebraic dual

Let G be a connected graph. An algebraic dual of G is a graph G^★ so that
G and G^★ have the same set of edges, any cycle

Cycle space

In graph theory, an area of mathematics, a cycle space is a vector space defined from an undirected graph; elements of the cycle space represent formal combinations of cycles in the graph....

 of G is a cut of G^★, and any cut of G is a cycle of G^★.
Every planar graph has an algebraic dual which is in general not unique (any dual defined by a plane embedding will do). The converse is actually true, as settled by Whitney:

A connected graph G is planar if and only if it has an algebraic dual.

The same fact can be expressed in the theory of matroid

Matroid

In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....

s: if M is the graphic matroid of a graph G, then the dual matroid of M is a graphic matroid if and only if G is planar. If G is planar, the dual matroid is the graphic matroid of the dual graph of G.

Weak dual

The weak dual of an embedded planar graph

Planar graph

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...

 is the subgraph of the dual graph whose vertices correspond to the bounded faces of the primal graph. A planar graph is outerplanar

Outerplanar graph

In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...

 if and only if its weak dual is a forest

Tree (graph theory)

In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...

, and a planar graph is a Halin graph

Halin graph

In graph theory, a mathematical discipline, a Halin graph is a planar graph constructed from a plane embedding of a tree with at least four vertices and with no vertices of degree 2, by connecting all the leaves of the tree with a cycle that passes around the tree in the natural cyclic order...

 if and only if its weak dual is biconnected

Biconnected graph

In the mathematical discipline of graph theory, a biconnected graph is a connected graph with no articulation vertices.In other words, a biconnected graph is connected and nonseparable, meaning that if any vertex were to be removed, the graph will remain connected.The property of being 2-connected...

and outerplanar. For any embedded planar graph G, let G⁺ be the multigraph formed by adding a single new vertex v in the unbounded face of G, and connecting v to each vertex of the outer face (multiple times, if a vertex appears multiple times on the boundary of the outer face); then, G is the weak dual of the planar dual of G⁺.