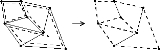
Cycle space
Encyclopedia
In graph theory
, an area of mathematics, a cycle space is a vector space
defined from an undirected graph; elements of the cycle space represent formal combinations of cycles
in the graph.
Cycle spaces allow one to use the tools of linear algebra
to study graphs. A cycle basis is a set of cycles that generates the cycle space.
-vector space if we take the symmetric difference
as addition, identity function
as negation, and empty set
as zero. The one-element sets form a basis
, so its dimension is equal to the number of edges of G. Because every element of this vector space is a subset of E, it can be regarded as an indicator function of type , then this vector space coincide with the free Z2-module
, then this vector space coincide with the free Z2-module
with basis E. This is the (binary) edge space of G.
An important subspace
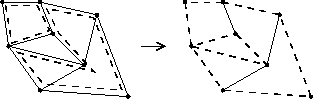
of the edge space is the (binary) cycle space. It is by definition the subspace generated by (the edge sets of) all the simple cycles of the graph. The addition of two
cycles (shown dashed) is illustrated in the figure.
Note that the result here (also shown dashed) is not a simple cycle but an edge-disjoint union of two simple cycles.
There are a number of basic results concerning the cycle space. The symmetric difference of two simple cycles is either a simple cycle or a union of edge-disjoint simple cycles. Using this observation, one can show that an edge set is in the cycle space if and only if it is a disjoint union of simple cycles. Phrased another way: the set F of edges is in the cycle space if and only if every vertex in the subgraph spanned by F has even degree.
It is not necessary to use all cycles to generate the cycle space: if G is connected and any spanning tree
T of G is given, then the fundamental cycles of T form a basis
of the cycle space, known as a cycle basis. The dimension of the cycle space of a connected graph is thus related to the number of vertices and edges of the graph. If the graph has n vertices and m edges then the dimension is m − n + 1. In a planar graph
, the set of interior faces of an embedding of the graph also provides a cycle basis.
An important application of the cycle space are Whitney's planarity criterion
and Mac Lane's planarity criterion
, which give an algebraic characterization of the planar graph
s.
ZE of functions from the edge set E to the integers. It is necessary (for the notation) to choose an arbitrary orientation of the graph in order to define the cycle space, but the definition does not depend on that choice. An integral cycle is a function such that the sum of values on edges oriented into a vertex x equals the sum of values on edges oriented out of x, for every vertex x. The set of integral cycles is a subgroup of the integral edge space. A cycle that never takes the value zero is called nowhere zero.
Reversing the orientation of an edge negates the value of a cycle on that edge. It is in this sense that the theory is independent of the arbitrary orientation. Given any one cycle, the orientation can be chosen so that cycle takes only nonnegative values.
An integral cycle whose maximum absolute value on any edge is less than k, a positive integer, is sometimes called a k-flow on G. W.T. Tutte developed an extensive theory of nowhere-zero k-flows that is in some ways dual to that of graph coloring
.
, abelian group
, or (most generally) commutative ring
(with unity) R replacing the integers. If R is a field, the cycle space is a vector space
over R with dimension m - n + c, where c is the number of connected components of G. If R is any commutative ring, the cycle space is a free R-module
with rank m - n + c.
When R is an abelian group such a cycle may also be called an R-flow on G. Nowhere-zero R-flows for a finite abelian group R of k elements are related to nowhere-zero integral k-flows in Tutte's theory. The number of nowhere-zero R-cycles is an evaluation of the Tutte polynomial
, dual to the number of proper colorings of the graph (Tutte, 1984, Section IX.4).
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, an area of mathematics, a cycle space is a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
defined from an undirected graph; elements of the cycle space represent formal combinations of cycles
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
in the graph.
Cycle spaces allow one to use the tools of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
to study graphs. A cycle basis is a set of cycles that generates the cycle space.
The binary cycle space
Let G be a finite simple undirected graph with edge set E. The power set of E becomes a Z2Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
-vector space if we take the symmetric difference
Symmetric difference
In mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
as addition, identity function
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
as negation, and empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
as zero. The one-element sets form a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
, so its dimension is equal to the number of edges of G. Because every element of this vector space is a subset of E, it can be regarded as an indicator function of type
 , then this vector space coincide with the free Z2-module
, then this vector space coincide with the free Z2-moduleFree module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
with basis E. This is the (binary) edge space of G.
An important subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of the edge space is the (binary) cycle space. It is by definition the subspace generated by (the edge sets of) all the simple cycles of the graph. The addition of two
cycles (shown dashed) is illustrated in the figure.
Note that the result here (also shown dashed) is not a simple cycle but an edge-disjoint union of two simple cycles.

There are a number of basic results concerning the cycle space. The symmetric difference of two simple cycles is either a simple cycle or a union of edge-disjoint simple cycles. Using this observation, one can show that an edge set is in the cycle space if and only if it is a disjoint union of simple cycles. Phrased another way: the set F of edges is in the cycle space if and only if every vertex in the subgraph spanned by F has even degree.
It is not necessary to use all cycles to generate the cycle space: if G is connected and any spanning tree
Spanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
T of G is given, then the fundamental cycles of T form a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of the cycle space, known as a cycle basis. The dimension of the cycle space of a connected graph is thus related to the number of vertices and edges of the graph. If the graph has n vertices and m edges then the dimension is m − n + 1. In a planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
, the set of interior faces of an embedding of the graph also provides a cycle basis.
An important application of the cycle space are Whitney's planarity criterion
Dual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
and Mac Lane's planarity criterion
Mac Lane's planarity criterion
In graph theory, Mac Lane's planarity criterion is a characterisation of planar graphs in terms of their cycle spaces. It states that a finite undirected graph is planar if and only if...
, which give an algebraic characterization of the planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s.
The integral cycle space
The foregoing development can be carried out over the integers, Z. The integral edge space is the abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
ZE of functions from the edge set E to the integers. It is necessary (for the notation) to choose an arbitrary orientation of the graph in order to define the cycle space, but the definition does not depend on that choice. An integral cycle is a function such that the sum of values on edges oriented into a vertex x equals the sum of values on edges oriented out of x, for every vertex x. The set of integral cycles is a subgroup of the integral edge space. A cycle that never takes the value zero is called nowhere zero.
Reversing the orientation of an edge negates the value of a cycle on that edge. It is in this sense that the theory is independent of the arbitrary orientation. Given any one cycle, the orientation can be chosen so that cycle takes only nonnegative values.
An integral cycle whose maximum absolute value on any edge is less than k, a positive integer, is sometimes called a k-flow on G. W.T. Tutte developed an extensive theory of nowhere-zero k-flows that is in some ways dual to that of graph coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
.
The cycle space over a field or commutative ring
The construction of the integral cycle space can be carried out for any fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, or (most generally) commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
(with unity) R replacing the integers. If R is a field, the cycle space is a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over R with dimension m - n + c, where c is the number of connected components of G. If R is any commutative ring, the cycle space is a free R-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
with rank m - n + c.
When R is an abelian group such a cycle may also be called an R-flow on G. Nowhere-zero R-flows for a finite abelian group R of k elements are related to nowhere-zero integral k-flows in Tutte's theory. The number of nowhere-zero R-cycles is an evaluation of the Tutte polynomial
Tutte polynomial
The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a polynomial in two variables which plays an important role in graph theory, a branch of mathematics and theoretical computer science...
, dual to the number of proper colorings of the graph (Tutte, 1984, Section IX.4).

