Bidimensionality
Encyclopedia
Bidimensionality theory characterizes a broad range of graph problems (bidimensional) that admit efficient approximate, fixed-parameter or kernel solutions in a broad range of graphs. These graph classes include planar graph
s, map graphs, bounded-genus
graphs and graphs excluding any fixed minor. In particular, bidimensionality theory builds on the Graph Minor Theory
of Robertson
and Seymour by extending the mathematical results and building new algorithmic tools. The theory was introduced in the work of Demaine
, Fomin, Hajiaghayi, and Thilikos.
is a subset of 
for some finite alphabet 
. An instance of a parameterized problem consists of (x,k), where k is called the parameter.
A parameterized problem
is minor-bidimensional if
Examples of minor-bidimensional problems are the parameterized versions of Vertex Cover
, Feedback Vertex Set
, Minimum Maximal Matching, and Longest Path
.
Let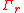
be the graph obtained from the 
-grid by
triangulating internal faces such that all internal vertices become of degree 6,
and then one corner of degree two joined by edges with all vertices
of the external face.
A parameterized problem
is contraction-bidimensional if
Examples of contraction-bidimensional problems are Dominating Set
, Connected Dominating Set
, Max-Leaf Spanning Tree, and Edge Dominating Set
|.
be a minor-bidimensional problem such that for any graph G excluding some fixed graph as a minor and of treewidth at most t, deciding whether 
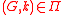can be done in time 
. Then for every graph G excluding some fixed graph as a minor, deciding whether 
can be done in time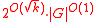 
. Similarly, for contraction-bidimensional problems, for graph G excluding some fixed apex graph
as a minor, inclusion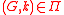
can be decided in time 
.
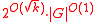Thus many bidimensional problems like Vertex Cover, Dominating Set, k-Path, are solvable in time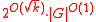
on graphs excluding some fixed graph as a minor.
) for many bidimensional problems.
If a minor (contraction) bidimensional problem has several additional properties then the problem poses Efficient Polynomial Time Approximation Scheme (EPTAS) on (apex) minor-free graphs.
In particular, by making use of Bidimensionality, it was shown that Feedback Vertex Set, Vertex Cover, Connected Vertex Cover, Cycle Packing, Diamond Hitting Set, Maximum Induced Forest, Maximum Induced Bipartite Subgraph and Maximum Induced Planar Subgraph admit an EPTAS on H-minor-free graphs. Edge Dominating Set, Dominating Set, r-Dominating Set, Connected Dominating Set, r-Scattered Set, Minimum Maximal Matching, Independent Set, Maximum Full-Degree Spanning Tree, Max Induced at most d-Degree Subgraph, Max Internal Spanning Tree, Induced Matching, Triangle Packing, Partial r-Dominating Set and Partial Vertex Cover admit an EPTAS on apex-minor-free graphs.
algorithm, that maps the input instance to an equivalent instance with at most O(k) vertices.
Every minor-bidimensional problem
with additional properties, namely, with the separation property and with finite integer index, has a linear vertex kernel on graphs excluding some fixed graph as a minor. Similarly, every contraction-bidimensional problem 
with the separation property and with finite integer index has a linear vertex kernel on graphs excluding some fixed apex graph
as a minor.
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s, map graphs, bounded-genus
Graph embedding
In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...
graphs and graphs excluding any fixed minor. In particular, bidimensionality theory builds on the Graph Minor Theory
Minor (graph theory)
In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....
of Robertson
Neil Robertson (mathematician)
G. Neil Robertson is a mathematician working mainly in topological graph theory, currently a distinguished professor at the Ohio State University. He earned his Ph.D. in 1969 at the University of Waterloo under his doctoral advisor William Tutte. According to the criteria of the Erdős Number...
and Seymour by extending the mathematical results and building new algorithmic tools. The theory was introduced in the work of Demaine
Erik Demaine
Erik D. Demaine , is a professor of Computer Science at the Massachusetts Institute of Technology.-Early life:...
, Fomin, Hajiaghayi, and Thilikos.
Definition
A parameterized problemParameterized complexity
Parameterized complexity is a branch of computational complexity theory in computer science that focuses on classifying computational problems according to their inherent difficulty with respect to multiple parameters of the input. The complexity of a problem is then measured as a function in those...
is a subset of for some finite alphabet . An instance of a parameterized problem consists of (x,k), where k is called the parameter.A parameterized problem
is minor-bidimensional if
- For any pair of graphs
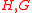, such that 
is a minor of 
and integer 
, 
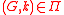yields that 
. In other words, contracting or deleting an edge in a graph 
cannot increase the parameter; and - there is
such that for every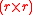 
-grid 
, 
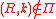for every 
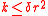. In other words, the value of the solution on 
should be at least 
.
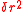Examples of minor-bidimensional problems are the parameterized versions of Vertex Cover
Vertex cover
In the mathematical discipline of graph theory, a vertex cover of a graph is a set of vertices such that each edge of the graph is incident to at least one vertex of the set....
, Feedback Vertex Set
Feedback vertex set
In the mathematical discipline of graph theory, a feedback vertex set of a graph is a set of vertices whose removal leaves a graph without cycles. In other words, each feedback vertex set contains at least one vertex of any cycle in the graph....
, Minimum Maximal Matching, and Longest Path
Longest path problem
In the mathematical discipline of graph theory, the longest path problem is the problem of finding a simple path of maximum length in a given graph. A path is called simple if it does not have any repeated vertices...
.
Let
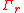be the graph obtained from the -grid bytriangulating internal faces such that all internal vertices become of degree 6,
and then one corner of degree two joined by edges with all vertices
of the external face.
A parameterized problem
is contraction-bidimensional if
- For any pair of graphs
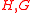, such that 
is a contraction of 
and integer 
, 
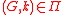yields that 
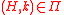. In other words, contracting an edge in a graph 
cannot increase the parameter; and - there is
such that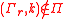 
for every 
.
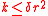Examples of contraction-bidimensional problems are Dominating Set
Dominating set
In graph theory, a dominating set for a graph G = is a subset D of V such that every vertex not in D is joined to at least one member of D by some edge...
, Connected Dominating Set
Connected dominating set
In graph theory, a connected dominated set and a maximum leaf spanning tree are two closely related structures defined on an undirected graph.-Definitions:A connected dominating set of a graph G is a set D of vertices with two properties:...
, Max-Leaf Spanning Tree, and Edge Dominating Set
Edge dominating set
In graph theory, an edge dominating set for a graph G = is a subset D ⊆ E such that every edge not in D is adjacent to at least one edge in D. An edge dominating set is also known as a line dominating set...
|.
Excluding Grid Theorems
All algorithmic applications of bidimensionality are based on the following combinatorial property: either the treewidth of a graph is small, or the graph contains a large grid as a minor or contraction. More precisely,- There is a function f such that every graph G excluding a fixed h-vertex graph as a minorMinor (graph theory)In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....
and of treewidth at least f(h)r contains (r x r)-grid as a minor. - There is a function g such that every graph G excluding a fixed h-vertex apex graphApex graphIn graph theory, a branch of mathematics, an apex graph is a graph that can be made planar by the removal of a single vertex. The deleted vertex is called an apex of the graph. We say an apex, not the apex because an apex graph may have more than one apex...
as a minor and of treewidth at least g(h) r can be edge-contracted to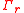
.
Subexponential parameterized algorithms
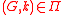Let be a minor-bidimensional problem such that for any graph G excluding some fixed graph as a minor and of treewidth at most t, deciding whether can be done in time . Then for every graph G excluding some fixed graph as a minor, deciding whether can be done in time 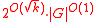. Similarly, for contraction-bidimensional problems, for graph G excluding some fixed apex graphApex graph
In graph theory, a branch of mathematics, an apex graph is a graph that can be made planar by the removal of a single vertex. The deleted vertex is called an apex of the graph. We say an apex, not the apex because an apex graph may have more than one apex...
as a minor, inclusion
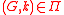can be decided in time 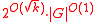.Thus many bidimensional problems like Vertex Cover, Dominating Set, k-Path, are solvable in time
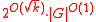on graphs excluding some fixed graph as a minor.Polynomial Time Approximation Schemes (PTAS)
Bidimensionality theory has been used to obtain Polynomial Time Approximation Schemes (PTASPolynomial-time approximation scheme
In computer science, a polynomial-time approximation scheme is a type of approximation algorithm for optimization problems ....
) for many bidimensional problems.
If a minor (contraction) bidimensional problem has several additional properties then the problem poses Efficient Polynomial Time Approximation Scheme (EPTAS) on (apex) minor-free graphs.
In particular, by making use of Bidimensionality, it was shown that Feedback Vertex Set, Vertex Cover, Connected Vertex Cover, Cycle Packing, Diamond Hitting Set, Maximum Induced Forest, Maximum Induced Bipartite Subgraph and Maximum Induced Planar Subgraph admit an EPTAS on H-minor-free graphs. Edge Dominating Set, Dominating Set, r-Dominating Set, Connected Dominating Set, r-Scattered Set, Minimum Maximal Matching, Independent Set, Maximum Full-Degree Spanning Tree, Max Induced at most d-Degree Subgraph, Max Internal Spanning Tree, Induced Matching, Triangle Packing, Partial r-Dominating Set and Partial Vertex Cover admit an EPTAS on apex-minor-free graphs.
Kernelization
A parameterized problem with a parameter k is said to admit a linear vertex kernel if there is a polynomial time reduction, called a kernelizationKernelization
In computer science, a kernelization is an efficient algorithm that preprocesses instances of decision problems by mapping them to equivalent instances with a guaranteed upper bound on the size of the output, called the kernel of the instance. Kernelization is often achieved by applying a set of...
algorithm, that maps the input instance to an equivalent instance with at most O(k) vertices.
Every minor-bidimensional problem
with additional properties, namely, with the separation property and with finite integer index, has a linear vertex kernel on graphs excluding some fixed graph as a minor. Similarly, every contraction-bidimensional problem with the separation property and with finite integer index has a linear vertex kernel on graphs excluding some fixed apex graphApex graph
In graph theory, a branch of mathematics, an apex graph is a graph that can be made planar by the removal of a single vertex. The deleted vertex is called an apex of the graph. We say an apex, not the apex because an apex graph may have more than one apex...
as a minor.