Vertex cover
Encyclopedia
In the mathematical
discipline of graph theory
, a vertex cover of a graph
is a set of vertices such that each edge of the graph is incident
to at least one vertex of the set.
The problem of finding a minimum vertex cover is a classical optimization problem
in computer science
and is a typical example of an NP-hard
optimization problem that has an approximation algorithm
. Its decision version
, the vertex cover problem, was one of Karp's 21 NP-complete problems
and is therefore a classical NP-complete
problem in computational complexity theory
. Furthermore, the vertex cover problem is fixed-parameter tractable and a central problem in parameterized complexity theory
.
The minimum vertex cover problem can be formulated as a half-integral linear program whose dual linear program is the maximum matching problem.
A minimum vertex cover is a vertex cover of smallest possible size. The vertex cover number
is the size of a minimum vertex cover. The following figure shows examples of minimum vertex covers in two graphs.
of finding a smallest vertex cover in a given graph.
If the problem is stated as a decision problem
, it is called the vertex cover problem:
The vertex cover problem is an NP-complete
problem: it was one of Karp's 21 NP-complete problems
. It is often used in computational complexity theory
as a starting point for NP-hard
ness proofs.
.
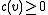The (weighted) minimum vertex cover problem can be formulated as the following integer linear program (ILP).
This ILP belongs to the more general class of ILPs for covering problem
s.
The integrality gap of this ILP is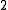
, so its relaxation gives a factor-
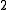approximation algorithm
for the minimum vertex cover problem.
Furthermore, the linear programming relaxation of that ILP is half-integral, that is, there exists an optimal solution for which each entry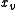
is either 0, 1/2, or 1.
variant of the vertex cover problem is NP-complete
, which means it is unlikely that there is an efficient algorithm to solve it exactly. NP-completeness can be proven by reduction from 3-satisfiability
or, as Karp did, by reduction from the clique problem
. Vertex cover remains NP-complete even in cubic graph
s and even in planar graph
s of degree at most 3.
For bipartite graph
s, the equivalence between vertex cover and maximum matching described by König's theorem
allows the bipartite vertex cover problem to be solved in polynomial time.
algorithm can solve the problem in time 2knO(1). Vertex cover is therefore fixed-parameter tractable, and if we are only interested in small k, we can solve the problem in polynomial time. One algorithmic technique that works here is called bounded search tree algorithm, and its idea is to repeatedly choose some vertex and recursively branch, with two cases at each step: place either the current vertex or all its neighbours into the vertex cover.
The algorithm for solving vertex cover that achieves the best asymptotic dependence on the parameter runs in time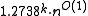
.
Under reasonable complexity-theoretic assumptions, namely the exponential time hypothesis
, this running time cannot be improved to 2o(k)nO(1).
However, for planar graph
s, and more generally, for graphs excluding some fixed graph as a minor, a vertex cover of size k can be found in time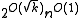
, i.e., the problem is subexponential fixed-parameter tractable. This algorithm is again optimal, in the sense that, under the exponential time hypothesis
, no algorithm can solve vertex cover on planar graphs in time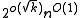
.
by repeatedly taking both endpoints of an edge into the vertex cover, then removing them from the graph. Put otherwise, we find a maximal matching M with a greedy algorithm and construct a vertex cover C that consists of all endpoints of the edges in M. In the following figure, a maximal matching M is marked with red, and the vertex cover C is marked with blue.
The set C constructed this way is a vertex cover: suppose that an edge e is not covered by C; then M ∪ {e} is a matching and e ∉ M, which is a contradiction with the assumption that M is maximal. Furthermore, if e = {u, v} ∈ M, then any vertex cover – including an optimal vertex cover – must contain u or v (or both); otherwise the edge e is not covered. That is, an optimal cover contains at least one endpoint of each edge in M; in total, the set C is at most 2 times as large as the optimal vertex cover.
This simple algorithm was discovered independently by Fanica Gavril and Mihalis Yannakakis.
More involved techniques show that there are approximation algorithms with a slightly better approximation factor. For example, an approximation algorithm with an approximation factor of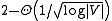
is known.
The minimum vertex cover problem is APX-complete
, that is, it cannot be approximated arbitrarily well unless P = NP.
Using techniques from the PCP theorem
, Dinur
and Safra
proved in 2005 that minimum vertex cover cannot be approximated within a factor of 1.3606 for any sufficiently large vertex degree unless P = NP. Moreover, if the unique games conjecture
is true then minimum vertex cover cannot be approximated within any constant factor better than 2.
Although finding the minimum-size vertex cover is equivalent to finding the maximum-size independent set, as described above, the two problems are not equivalent in an approximation-preserving way: The Independent Set problem has no constant-factor approximation unless P = NP.
s which is often just called vertex cover for hypergraphs and, in a more combinatorial context, transversal.
The notions of hitting set and set cover are equivalent.
Formally, let H = (V, E) be a hypergraph with vertex set V and hyperedge set E. Then a set S ⊆ V is called hitting set of H if, for all edges e ∈ E, it holds S ∩ e ≠ ∅.
The computational problems minimum hitting set and hitting set are defined as in the case of graphs. Note that we get back the case of vertex covers for simple graphs if the maximum size of the hyperedges is 2.
If that size is restricted to d, the problem of finding a minimum d-hitting set permits a d-approximation
algorithm. Assuming the unique games conjecture
, this is the best constant-factor algorithm that is possible and otherwise there is the possibility of improving the approximation to d − 1.
The hitting set problem is W[2]-complete for the parameter OPT, that is, it is unlikely that there is an algorithm that runs in time f(OPT)nO(1) where OPT is the cardinality of the smallest hitting set.
The hitting set problem is fixed-parameter tractable for the parameter OPT + d, where d is the size of the largest edge of the hypergraph. More specifically, there is an algorithm for hitting set that runs in time dOPTnO(1).
:
An instance of set cover can be viewed as an arbitrary bipartite graph, with sets represented by vertices on the left, elements of the universe represented by vertices on the right, and edges representing the inclusion of elements in sets. The task is then to find a minimum cardinality subset of left-vertices which covers all of the right-vertices. In the hitting set problem, the objective is to cover the left-vertices using a minimum subset of the right vertices. Converting from one problem to the other is therefore achieved by interchanging the two sets of vertices.
s. In this case, each time global memory is written, the current thread and set of locks held by that thread are stored. Under lockset-based detection, if later another thread writes to that location and there is not a race, it must be because it holds at least one lock in common with each of the previous writes. Thus the size of the hitting set represents the minimum lock set size to be race-free. This is useful in eliminating redundant write events, since large lock sets are considered unlikely in practice.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
discipline of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a vertex cover of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
is a set of vertices such that each edge of the graph is incident
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
to at least one vertex of the set.
The problem of finding a minimum vertex cover is a classical optimization problem
Optimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and is a typical example of an NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
optimization problem that has an approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
. Its decision version
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
, the vertex cover problem, was one of Karp's 21 NP-complete problems
Karp's 21 NP-complete problems
One of the most important results in computational complexity theory was Stephen Cook's 1971 demonstration of the first NP-complete problem, the boolean satisfiability problem...
and is therefore a classical NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem in computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
. Furthermore, the vertex cover problem is fixed-parameter tractable and a central problem in parameterized complexity theory
Parameterized complexity
Parameterized complexity is a branch of computational complexity theory in computer science that focuses on classifying computational problems according to their inherent difficulty with respect to multiple parameters of the input. The complexity of a problem is then measured as a function in those...
.
The minimum vertex cover problem can be formulated as a half-integral linear program whose dual linear program is the maximum matching problem.
Definition
Formally, a vertex cover of a graph G is a set C of vertices such that each edge of G is incident to at least one vertex in C. The set C is said to cover the edges of G. The following figure shows examples of vertex covers in two graphs (the set C is marked with red).A minimum vertex cover is a vertex cover of smallest possible size. The vertex cover number
is the size of a minimum vertex cover. The following figure shows examples of minimum vertex covers in two graphs.Examples
- The set of all vertices is a vertex cover.
- The endpoints of any maximal matching form a vertex cover.
- The complete bipartite graphComplete bipartite graphIn the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
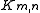has a minimum vertex cover of size 
.
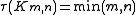Properties
- A set of vertices is a vertex cover, if and only if its complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
is an independent setIndependent set (graph theory)In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
. An immediate consequence is: - The number of vertices of a graph is equal to its vertex cover number plus the size of a maximum independent set (GallaiTibor GallaiTibor Gallai was a Hungarian mathematician. He worked in combinatorics, especially in graph theory, and was a lifelong friend and collaborator of Paul Erdős. He was a student of Dénes König and an advisor of László Lovász...
1959).
Computational problem
The minimum vertex cover problem is the optimization problemOptimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
of finding a smallest vertex cover in a given graph.
- INSTANCE: Graph
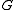
- OUTPUT: Smallest number
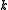such that 
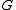has a vertex cover of size 
.
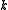If the problem is stated as a decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
, it is called the vertex cover problem:
- INSTANCE: Graph
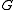and positive integer 
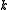. - QUESTION: Does
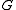have a vertex cover of size at most 
?
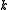The vertex cover problem is an NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem: it was one of Karp's 21 NP-complete problems
Karp's 21 NP-complete problems
One of the most important results in computational complexity theory was Stephen Cook's 1971 demonstration of the first NP-complete problem, the boolean satisfiability problem...
. It is often used in computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
as a starting point for NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
ness proofs.
ILP formulation
Assume that every vertex has an associated cost of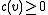.The (weighted) minimum vertex cover problem can be formulated as the following integer linear program (ILP).
| minimize |  |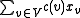
(minimize the total cost) | ||
| subject to |  |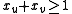
for all  |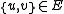
(cover every edge of the graph) | |
 |
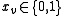for all  . |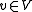
(every vertex is either in the vertex cover or not) |
This ILP belongs to the more general class of ILPs for covering problem
Covering problem
In combinatorics and computer science, covering problems are computational problems that ask whether a certain combinatorial structure 'covers' another, or how large the structure has to be to do that....
s.
The integrality gap of this ILP is
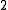, so its relaxation gives a factor- 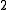approximation algorithmApproximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
for the minimum vertex cover problem.
Furthermore, the linear programming relaxation of that ILP is half-integral, that is, there exists an optimal solution for which each entry
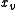is either 0, 1/2, or 1.Exact evaluation
The decisionDecision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
variant of the vertex cover problem is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
, which means it is unlikely that there is an efficient algorithm to solve it exactly. NP-completeness can be proven by reduction from 3-satisfiability
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
or, as Karp did, by reduction from the clique problem
Clique problem
In computer science, the clique problem refers to any of the problems related to finding particular complete subgraphs in a graph, i.e., sets of elements where each pair of elements is connected....
. Vertex cover remains NP-complete even in cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
s and even in planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s of degree at most 3.
For bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
s, the equivalence between vertex cover and maximum matching described by König's theorem
König's theorem (graph theory)
In the mathematical area of graph theory, König's theorem, proved by Dénes Kőnig in 1931, describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs...
allows the bipartite vertex cover problem to be solved in polynomial time.
Fixed-parameter tractability
An exhaustive searchBrute-force search
In computer science, brute-force search or exhaustive search, also known as generate and test, is a trivial but very general problem-solving technique that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem's...
algorithm can solve the problem in time 2knO(1). Vertex cover is therefore fixed-parameter tractable, and if we are only interested in small k, we can solve the problem in polynomial time. One algorithmic technique that works here is called bounded search tree algorithm, and its idea is to repeatedly choose some vertex and recursively branch, with two cases at each step: place either the current vertex or all its neighbours into the vertex cover.
The algorithm for solving vertex cover that achieves the best asymptotic dependence on the parameter runs in time
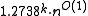.Under reasonable complexity-theoretic assumptions, namely the exponential time hypothesis
Exponential time hypothesis
In computational complexity theory, the exponential time hypothesis is an unproven computational hardness assumption formalized by stating that 3-SAT cannot be solved in subexponential time in the worst case. The exponential time hypothesis, if true, would imply that P ≠ NP...
, this running time cannot be improved to 2o(k)nO(1).
However, for planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s, and more generally, for graphs excluding some fixed graph as a minor, a vertex cover of size k can be found in time
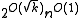, i.e., the problem is subexponential fixed-parameter tractable. This algorithm is again optimal, in the sense that, under the exponential time hypothesisExponential time hypothesis
In computational complexity theory, the exponential time hypothesis is an unproven computational hardness assumption formalized by stating that 3-SAT cannot be solved in subexponential time in the worst case. The exponential time hypothesis, if true, would imply that P ≠ NP...
, no algorithm can solve vertex cover on planar graphs in time
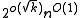.Approximate evaluation
One can find a factor-2 approximationApproximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
by repeatedly taking both endpoints of an edge into the vertex cover, then removing them from the graph. Put otherwise, we find a maximal matching M with a greedy algorithm and construct a vertex cover C that consists of all endpoints of the edges in M. In the following figure, a maximal matching M is marked with red, and the vertex cover C is marked with blue.
The set C constructed this way is a vertex cover: suppose that an edge e is not covered by C; then M ∪ {e} is a matching and e ∉ M, which is a contradiction with the assumption that M is maximal. Furthermore, if e = {u, v} ∈ M, then any vertex cover – including an optimal vertex cover – must contain u or v (or both); otherwise the edge e is not covered. That is, an optimal cover contains at least one endpoint of each edge in M; in total, the set C is at most 2 times as large as the optimal vertex cover.
This simple algorithm was discovered independently by Fanica Gavril and Mihalis Yannakakis.
More involved techniques show that there are approximation algorithms with a slightly better approximation factor. For example, an approximation algorithm with an approximation factor of
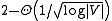is known.Inapproximability
No better constant-factor approximation algorithm than the above one is known.The minimum vertex cover problem is APX-complete
APX
In complexity theory the class APX is the set of NP optimization problems that allow polynomial-time approximation algorithms with approximation ratio bounded by a constant...
, that is, it cannot be approximated arbitrarily well unless P = NP.
Using techniques from the PCP theorem
PCP theorem
In computational complexity theory, the PCP theorem states that every decision problem in the NP complexity class has probabilistically checkable proofs of constant query complexity and logarithmic randomness complexity .The PCP theorem says that for some universal constant K, for every...
, Dinur
Irit Dinur
Irit Dinur is an Israeli mathematician. She is currently professor of computer science at the Weizmann Institute of Science. Her research is in foundations of computer science and in combinatorics, especially probabilistically checkable proofs, hardness of approximation. She graduated from the...
and Safra
Shmuel Safra
Shmuel Safra is a Professor of Computer Science at Tel Aviv University, Israel. Born in Jerusalem.Safra's research areas include Complexity Theory and Automata Theory...
proved in 2005 that minimum vertex cover cannot be approximated within a factor of 1.3606 for any sufficiently large vertex degree unless P = NP. Moreover, if the unique games conjecture
Unique games conjecture
In computational complexity theory, the Unique Games Conjecture is a conjecture made by Subhash Khot in 2002. The conjecture postulates that the problem of determining the value of a certain type of game, known as a unique game, has NP-hard algorithmic complexity...
is true then minimum vertex cover cannot be approximated within any constant factor better than 2.
Although finding the minimum-size vertex cover is equivalent to finding the maximum-size independent set, as described above, the two problems are not equivalent in an approximation-preserving way: The Independent Set problem has no constant-factor approximation unless P = NP.
Vertex cover in hypergraphs
Given a collection of sets, a set which intersects all sets in the collection in at least one element is called a hitting set, and a simple NP-complete problem is to find a hitting set of smallest size or minimum hitting set. By mapping the sets in the collection onto hyperedges, this can be understood as a natural generalization of the vertex cover problem to hypergraphHypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
s which is often just called vertex cover for hypergraphs and, in a more combinatorial context, transversal.
The notions of hitting set and set cover are equivalent.
Formally, let H = (V, E) be a hypergraph with vertex set V and hyperedge set E. Then a set S ⊆ V is called hitting set of H if, for all edges e ∈ E, it holds S ∩ e ≠ ∅.
The computational problems minimum hitting set and hitting set are defined as in the case of graphs. Note that we get back the case of vertex covers for simple graphs if the maximum size of the hyperedges is 2.
If that size is restricted to d, the problem of finding a minimum d-hitting set permits a d-approximation
K-approximation of k-hitting set
In computer science, k-approximation of k-hitting set is an approximation algorithm for weighted hitting set. The input is a collection S of subsets of some universe T and a mapping W from S to non-negative numbers called the weights of the elements of S. In k-hitting set the size of the sets in S...
algorithm. Assuming the unique games conjecture
Unique games conjecture
In computational complexity theory, the Unique Games Conjecture is a conjecture made by Subhash Khot in 2002. The conjecture postulates that the problem of determining the value of a certain type of game, known as a unique game, has NP-hard algorithmic complexity...
, this is the best constant-factor algorithm that is possible and otherwise there is the possibility of improving the approximation to d − 1.
Fixed-parameter tractability
For the hitting set problem, different parameterizations make sense.The hitting set problem is W[2]-complete for the parameter OPT, that is, it is unlikely that there is an algorithm that runs in time f(OPT)nO(1) where OPT is the cardinality of the smallest hitting set.
The hitting set problem is fixed-parameter tractable for the parameter OPT + d, where d is the size of the largest edge of the hypergraph. More specifically, there is an algorithm for hitting set that runs in time dOPTnO(1).
Hitting set and set cover
The hitting set problem is equivalent to the set cover problemSet cover problem
The set covering problem is a classical question in computer science and complexity theory.It is a problem "whose study has led to the development of fundamental techniques for the entire field" of approximation algorithms...
:
An instance of set cover can be viewed as an arbitrary bipartite graph, with sets represented by vertices on the left, elements of the universe represented by vertices on the right, and edges representing the inclusion of elements in sets. The task is then to find a minimum cardinality subset of left-vertices which covers all of the right-vertices. In the hitting set problem, the objective is to cover the left-vertices using a minimum subset of the right vertices. Converting from one problem to the other is therefore achieved by interchanging the two sets of vertices.
Applications
An example of a practical application involving the hitting set problem arises in efficient dynamic detection of race conditionRace condition
A race condition or race hazard is a flaw in an electronic system or process whereby the output or result of the process is unexpectedly and critically dependent on the sequence or timing of other events...
s. In this case, each time global memory is written, the current thread and set of locks held by that thread are stored. Under lockset-based detection, if later another thread writes to that location and there is not a race, it must be because it holds at least one lock in common with each of the previous writes. Thus the size of the hitting set represents the minimum lock set size to be race-free. This is useful in eliminating redundant write events, since large lock sets are considered unlikely in practice.