
K-approximation of k-hitting set
Encyclopedia
In computer science
, k-approximation of k-hitting set is an approximation algorithm
for weighted hitting set. The input is a collection
S of subset
s of some universe T and a mapping
W from S to non-negative numbers called the weights of the elements of S. In k-hitting set the size of the sets in S cannot be larger than k. That is,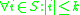 . The problem is now to pick some subset T
. The problem is now to pick some subset T' of T such that every set in S contains some element of T' , and such that the total weight of all elements in T' is as small as possible.
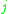 in S is maintained a price,
in S is maintained a price, 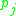 , which is initially 0. For an element a in T, let S(a) be the collection of sets from S containing a. During the algorithm the following invariant is kept
, which is initially 0. For an element a in T, let S(a) be the collection of sets from S containing a. During the algorithm the following invariant is kept
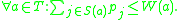
We say that an element a from T is tight if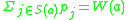 . The main part of the algorithm consists of a loop: As long as there is a set in S that contains an element from T which is not tight, the price of this set is increased as much as possible without violating the invariant above. When this loop exits, all sets contain some tight element. Pick all the tight elements to be the hitting set.
. The main part of the algorithm consists of a loop: As long as there is a set in S that contains an element from T which is not tight, the price of this set is increased as much as possible without violating the invariant above. When this loop exits, all sets contain some tight element. Pick all the tight elements to be the hitting set.
Note that for any hitting set T* and any prices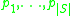 where the invariant from the algorithm is true, the total weight of the hitting set is an upper limit to the sum over all members of T* of the sum of the prices of sets containing this element, that is:
where the invariant from the algorithm is true, the total weight of the hitting set is an upper limit to the sum over all members of T* of the sum of the prices of sets containing this element, that is:  . This follows from the invariant property. Further, since the price of every set must occur at least once on the left hand side, we get
. This follows from the invariant property. Further, since the price of every set must occur at least once on the left hand side, we get 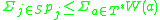 . Especially, this property is true for the optimal hitting set.
. Especially, this property is true for the optimal hitting set.
Further, for the hitting set H returned from the algorithm above, we have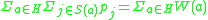 . Since any price
. Since any price 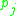 can appear at most k times in the left-hand side (since subsets of S can contain no more than k element from T) we get
can appear at most k times in the left-hand side (since subsets of S can contain no more than k element from T) we get  Combined with the previous paragraph we get
Combined with the previous paragraph we get 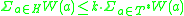 , where T* is the optimal hitting set. This is exactly the guarantee that it is a k-approximation algorithm.
, where T* is the optimal hitting set. This is exactly the guarantee that it is a k-approximation algorithm.
to a linear programming
algorithm. For an explanation see http://algo.inria.fr/seminars/sem00-01/vazirani.html.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, k-approximation of k-hitting set is an approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
for weighted hitting set. The input is a collection
Collection (computing)
In computer science, a collection is a grouping of some variable number of data items that have some shared significance to the problem being solved and need to be operated upon together in some controlled fashion. Generally, the data items will be of the same type or, in languages supporting...
S of subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of some universe T and a mapping
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
W from S to non-negative numbers called the weights of the elements of S. In k-hitting set the size of the sets in S cannot be larger than k. That is,
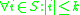 . The problem is now to pick some subset T
. The problem is now to pick some subset TThe algorithm
For each set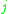 in S is maintained a price,
in S is maintained a price, 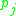 , which is initially 0. For an element a in T, let S(a) be the collection of sets from S containing a. During the algorithm the following invariant is kept
, which is initially 0. For an element a in T, let S(a) be the collection of sets from S containing a. During the algorithm the following invariant is kept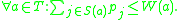
We say that an element a from T is tight if
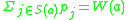 . The main part of the algorithm consists of a loop: As long as there is a set in S that contains an element from T which is not tight, the price of this set is increased as much as possible without violating the invariant above. When this loop exits, all sets contain some tight element. Pick all the tight elements to be the hitting set.
. The main part of the algorithm consists of a loop: As long as there is a set in S that contains an element from T which is not tight, the price of this set is increased as much as possible without violating the invariant above. When this loop exits, all sets contain some tight element. Pick all the tight elements to be the hitting set.Correctness
The algorithm always terminates because in each iteration of the loop the price of some set in S is increased enough to make one more element from T tight. If it cannot increase any price, it exits. It runs in polynomial time because the loop will not make more iterations than the number of elements in the union of all the sets of S. It returns a hitting set, because when the loop exits, all sets in S contain a tight element from T, and the set of these tight elements are returned.Note that for any hitting set T* and any prices
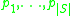 where the invariant from the algorithm is true, the total weight of the hitting set is an upper limit to the sum over all members of T* of the sum of the prices of sets containing this element, that is:
where the invariant from the algorithm is true, the total weight of the hitting set is an upper limit to the sum over all members of T* of the sum of the prices of sets containing this element, that is:  . This follows from the invariant property. Further, since the price of every set must occur at least once on the left hand side, we get
. This follows from the invariant property. Further, since the price of every set must occur at least once on the left hand side, we get 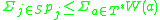 . Especially, this property is true for the optimal hitting set.
. Especially, this property is true for the optimal hitting set.Further, for the hitting set H returned from the algorithm above, we have
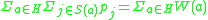 . Since any price
. Since any price 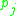 can appear at most k times in the left-hand side (since subsets of S can contain no more than k element from T) we get
can appear at most k times in the left-hand side (since subsets of S can contain no more than k element from T) we get  Combined with the previous paragraph we get
Combined with the previous paragraph we get 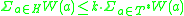 , where T* is the optimal hitting set. This is exactly the guarantee that it is a k-approximation algorithm.
, where T* is the optimal hitting set. This is exactly the guarantee that it is a k-approximation algorithm.Relation to linear programming
This algorithm is an instance of the primal-dual method, also called the pricing method. The intuition is that it is dualDuality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
to a linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
algorithm. For an explanation see http://algo.inria.fr/seminars/sem00-01/vazirani.html.

