Hypergraph
Encyclopedia
In mathematics
, a hypergraph is a generalization of a graph
, where an edge
can connect any number of vertices
. Formally, a hypergraph
is a pair 
where 
is a set of elements, called nodes or vertices, and 
is a set of non-empty subsets of 
called hyperedges or links. Therefore, 
is a subset of 
, where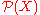 
is the power set of 
.
While graph edges are pairs of nodes, hyperedges are arbitrary sets of nodes, and can therefore contain an arbitrary number of nodes. However, it is often useful to study hypergraphs where all hyperedges have the same cardinality: a k-uniform hypergraph is a hypergraph such that all its hyperedges have size k. (In other words, it is a collection of sets of size k.) So a 2-uniform hypergraph is a graph, a 3-uniform hypergraph is a collection of triples, and so on.
A hypergraph is also called a set system or a family of sets drawn from the universal set X. Hypergraphs can be viewed as incidence structure
s and vice versa. In particular, there is a Levi graph
corresponding to every hypergraph, and vice versa. In computational geometry
, a hypergraph may be called a range space and the hyperedges are called ranges.
In cooperative game
theory, hypergraphs are called simple games (voting games); this notion is applied to solve problems in social choice theory
.
Special cases of hypergraphs include the clutter, where no edge appears as a subset of another edge; and the abstract simplicial complex
, which contains all subsets of every edge.
The collection of hypergraphs is a category
with hypergraph homomorphism
s as morphism
s.
Let
be the hypergraph consisting of vertices
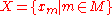
that is, the vertices are indexed by an index
, and the edge set is
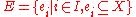
with the edges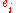
indexed by an index 
.
A subhypergraph is a hypergraph with some vertices removed. Formally, the subhypergraph
induced by a subset 
of 
is defined as
The partial hypergraph is a hypergraph with some edges removed. Given a subset
of the index set 
, the partial hypergraph generated by 
is the hypergraph
Given a subset
, the section hypergraph is the partial hypergraph
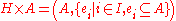
The dual
of 
is a hypergraph whose vertices and edges are interchanged, so that the vertices are given by 
and whose edges are given by 
where
When a notion of equality is properly defined, as done below, the operation of taking the dual of a hypergraph is an involution, i.e.,
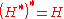
A connected graph G with the same vertex set as a connected hypergraph H is a host graph for H if every hyperedge of H induces a connected subgraph in G. For a disconnected hypergraph H, G is a host graph if there is a bijection between the connected components
of G and of H, such that each connected component G' of G is a host of the corresponding H' .
The primal graph of a hypergraph is the graph with the same vertices of the hypergraph, and edges between all pairs of vertices contained in the same hyperedge. The primal graph is sometimes also known as the Gaifman graph of the hypergraph.
BG as follows: the sets X and E are the partitions of BG, and (x1, e1) are connected with an edge if and only if vertex x1 is contained in edge e1 in H. Conversely, any bipartite graph with fixed parts and no unconnected nodes in the second part represents some hypergraph in the manner described above. This bipartite graph is also called incidence graph.
is a map from the vertex set of one hypergraph to another such that each edge maps to one other edge.
A hypergraph
is isomorphic to a hypergraph 
, written as 
if there exists a bijection
and a permutation
of 
such that
The bijection
is then called the isomorphism
of the graphs. Note that
if and only if 
.
When the edges of a hypergraph are explicitly labeled, one has the additional notion of strong isomorphism. One says that
is strongly isomorphic to 
if the permutation is the identity. One then writes 
. Note that all strongly isomorphic graphs are isomorphic, but not vice-versa.
When the vertices of a hypergraph are explicitly labeled, one has the notions of equivalence, and also of equality. One says that
is equivalent to 
, and writes 
if the isomorphism 
has
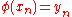
and
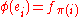
Note that
if and only if 
If, in addition, the permutation
is the identity, one says that 
equals 
, and writes 
. Note that, with this definition of equality, graphs are self-dual:
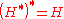
A hypergraph automorphism
is an isomorphism from a vertex set into itself, that is a relabeling of vertices. The set of automorphisms of a hypergraph H (= (X, E)) is a group
under composition, called the automorphism group of the hypergraph and written Aut(H).
with edges
and
Then clearly
and 
are isomorphic (with 
, etc.), but they are not strongly isomorphic. So, for example, in 
, vertex 
meets edges 1, 4 and 6, so that,
In graph
, there does not exist any vertex that meets edges 1, 4 and 6:
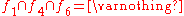
In this example,
and 
are equivalent, 
, and the duals are strongly isomorphic: 
.
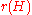of a hypergraph 
is the maximum cardinality of any of the edges in the hypergraph. If all edges have the same cardinality k, the hypergraph is said to be uniform or k-uniform, or is called a k-hypergraph. A graph is just a 2-uniform hypergraph.
The degree d(v) of a vertex v is the number of edges that contain it. H is k-regular if every vertex has degree k.
The dual of a uniform hypergraph is regular and vice-versa.
Two vertices x and y of H are called symmetric if there exists an automorphism such that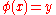
. Two edges 
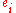and 
are said to be symmetric if there exists an automorphism such that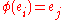 
.
A hypergraph is said to be vertex-transitive (or vertex-symmetric) if all of its vertices are symmetric. Similarly, a hypergraph is edge-transitive if all edges are symmetric. If a hypergraph is both edge- and vertex-symmetric, then the hypergraph is simply transitive.
Because of hypergraph duality, the study of edge-transitivity is identical to the study of vertex-transitivity.
that has nonempty intersection
with every edge. A transversal T is called minimal if no proper subset of T is a transversal. The transversal hypergraph of H is the hypergraph (X, F) whose edge set F consists of all minimal transversals of H. Computing the transversal
hypergraph has applications in machine learning
and other fields of computer science
, as game theory
, indexing of database
s, SAT problem
, data mining
and optimization
.
and 
. Every hypergraph has an 
incidence matrix
where
The transpose
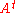of the incidence
matrix defines a hypergraph
called the dual of 
, where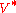 
is an m-element set and 
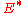is an n-element set of subsets of 
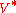. For 
and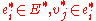 
if and only if
.
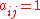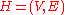be a hypergraph such that 
. Then 
is a proper colouring of 
if and only if, for all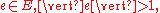 
there exists 
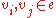such that 
.
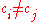In other words: For every edge in the graph having at least two nodes as endpoints, the nodes this edge connects are not all of the same color.
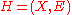, there exists a partition
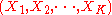
of the vertex set
such that the subhypergraph 
generated by 
is transitive for each 
, and such that
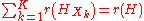
where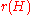
is the rank of H.
As a corollary, an edge-transitive hypergraph that is not vertex-transitive is bicolorable.
Graph partitioning (and in particular, hypergraph partitioning) has many applications to IC design and parallel computing.
s and concepts involving graphs also hold for hypergraphs. Ramsey's theorem
and Line graph of a hypergraph are typical examples. Some methods for studying symmetries of graphs extend to hypergraphs.
Two prominent theorems are the Erdős–Ko–Rado theorem and the Kruskal–Katona theorem on uniform hypergraphs.
In one possible visual representation for hypergraphs, similar to the standard graph drawing
style in which curves in the plane are used to depict graph edges, a hypergraph's vertices are depicted as points, disks, or boxes, and its hyperedges are depicted as trees that have the vertices as their leaves. If the vertices are represented as points, the hyperedges may also be shown as smooth curves that connect sets of points, or as simple closed curves that enclose sets of points.
In another style of hypergraph visualization, the subdivision model of hypergraph drawing, the plane is subdivided into regions, each of which represents a single vertex of the hypergraph. The hyperedges of the hypergraph are represented by contiguous subsets of these regions, which may be indicated by coloring, by drawing outlines around them, or both. An order-n Venn diagram
, for instance, may be viewed as a subdivision drawing of a hypergraph with n hyperedges (the curves defining the diagram) and 2n − 1 vertices (represented by the regions into which these curves subdivide the plane). In contrast with the polynomial-time recognition of planar graph
s, it is NP-complete
to determine whether a hypergraph has a planar subdivision drawing, but the existence of a drawing of this type may be tested efficiently when the adjacency pattern of the regions is constrained to be a path, cycle, or tree.
, since it is not transitive. The graph corresponding to the Levi graph of this generalization is a directed acyclic graph
. Consider, for example, the generalized hypergraph whose vertex set is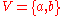
and whose edges are 
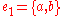and 
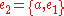. Then, although 
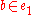and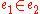 
, it is not true that 
. However, the transitive closure
of set membership for such hypergraphs does induce a partial order, and "flattens" the hypergraph into a partially ordered set
.
Alternately, edges can be allowed to point at other edges, (irrespective of the requirement that the edges be ordered as directed, acyclic graphs). This allows graphs with edge-loops, which need not contain vertices at all. For example, consider the generalized hypergraph consisting of two edges
and 
, and 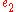zero vertices, so that 
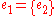and 
. As this loop is infinitely recursive, sets that are the edges violate the axiom of foundation. In particular, there is no transitive closure of set membership for such hypergraphs. Although such structures may seem strange at first, they can be readily understood by noting that the equivalent generalization of their Levi graph is no longer bipartite
, but is rather just some general directed graph
.
The generalized incidence matrix for such hypergraphs is, by definition, a square matrix, of a rank equal to the total number of vertices plus edges. Thus, for the above example, the incidence matrix
is simply
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a hypergraph is a generalization of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, where an edge
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
can connect any number of vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
. Formally, a hypergraph
is a pair where is a set of elements, called nodes or vertices, and is a set of non-empty subsets of called hyperedges or links. Therefore, is a subset of , where 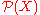is the power set of .While graph edges are pairs of nodes, hyperedges are arbitrary sets of nodes, and can therefore contain an arbitrary number of nodes. However, it is often useful to study hypergraphs where all hyperedges have the same cardinality: a k-uniform hypergraph is a hypergraph such that all its hyperedges have size k. (In other words, it is a collection of sets of size k.) So a 2-uniform hypergraph is a graph, a 3-uniform hypergraph is a collection of triples, and so on.
A hypergraph is also called a set system or a family of sets drawn from the universal set X. Hypergraphs can be viewed as incidence structure
Incidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
s and vice versa. In particular, there is a Levi graph
Levi graph
In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for...
corresponding to every hypergraph, and vice versa. In computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
, a hypergraph may be called a range space and the hyperedges are called ranges.
In cooperative game
Cooperative game
In game theory, a cooperative game is a game where groups of players may enforce cooperative behaviour, hence the game is a competition between coalitions of players, rather than between individual players...
theory, hypergraphs are called simple games (voting games); this notion is applied to solve problems in social choice theory
Social choice theory
Social choice theory is a theoretical framework for measuring individual interests, values, or welfares as an aggregate towards collective decision. A non-theoretical example of a collective decision is passing a set of laws under a constitution. Social choice theory dates from Condorcet's...
.
Special cases of hypergraphs include the clutter, where no edge appears as a subset of another edge; and the abstract simplicial complex
Abstract simplicial complex
In mathematics, an abstract simplicial complex is a purely combinatorial description of the geometric notion of a simplicial complex, consisting of a family of finite sets closed under the operation of taking subsets...
, which contains all subsets of every edge.
The collection of hypergraphs is a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
with hypergraph homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s as morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s.
Terminology
Because hypergraph links can have any cardinality, there are multiple, distinct notions of the concept of a subgraph: subhypergraphs, partial hypergraphs and section hypergraphs.Let
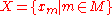
be the hypergraph consisting of verticesthat is, the vertices are indexed by an index
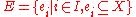
, and the edge set iswith the edges
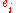indexed by an index .A subhypergraph is a hypergraph with some vertices removed. Formally, the subhypergraph
induced by a subset of is defined asThe partial hypergraph is a hypergraph with some edges removed. Given a subset
of the index set , the partial hypergraph generated by is the hypergraphGiven a subset
, the section hypergraph is the partial hypergraph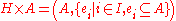The dual
of is a hypergraph whose vertices and edges are interchanged, so that the vertices are given by and whose edges are given by whereWhen a notion of equality is properly defined, as done below, the operation of taking the dual of a hypergraph is an involution, i.e.,
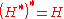
A connected graph G with the same vertex set as a connected hypergraph H is a host graph for H if every hyperedge of H induces a connected subgraph in G. For a disconnected hypergraph H, G is a host graph if there is a bijection between the connected components
Connected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
of G and of H, such that each connected component G
The primal graph of a hypergraph is the graph with the same vertices of the hypergraph, and edges between all pairs of vertices contained in the same hyperedge. The primal graph is sometimes also known as the Gaifman graph of the hypergraph.
Bipartite graph model
A hypergraph H may be represented by a bipartite graphBipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
BG as follows: the sets X and E are the partitions of BG, and (x1, e1) are connected with an edge if and only if vertex x1 is contained in edge e1 in H. Conversely, any bipartite graph with fixed parts and no unconnected nodes in the second part represents some hypergraph in the manner described above. This bipartite graph is also called incidence graph.
Isomorphism and equality
A hypergraph homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
is a map from the vertex set of one hypergraph to another such that each edge maps to one other edge.
A hypergraph
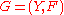is isomorphic to a hypergraph , written as if there exists a bijectionBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
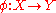
and a permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of such thatThe bijection
is then called the isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
of the graphs. Note that
if and only if .When the edges of a hypergraph are explicitly labeled, one has the additional notion of strong isomorphism. One says that
is strongly isomorphic to if the permutation is the identity. One then writes . Note that all strongly isomorphic graphs are isomorphic, but not vice-versa.When the vertices of a hypergraph are explicitly labeled, one has the notions of equivalence, and also of equality. One says that
is equivalent to , and writes if the isomorphism has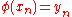and
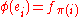
Note that
if and only if If, in addition, the permutation
is the identity, one says that equals , and writes . Note that, with this definition of equality, graphs are self-dual: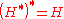A hypergraph automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
is an isomorphism from a vertex set into itself, that is a relabeling of vertices. The set of automorphisms of a hypergraph H (= (X, E)) is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under composition, called the automorphism group of the hypergraph and written Aut(H).
Examples
Consider the hypergraph with edgesand
Then clearly
and are isomorphic (with , etc.), but they are not strongly isomorphic. So, for example, in , vertex meets edges 1, 4 and 6, so that,In graph
, there does not exist any vertex that meets edges 1, 4 and 6: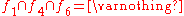In this example,
and are equivalent, , and the duals are strongly isomorphic: .Symmetric hypergraphs
The rank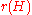 of a hypergraph is the maximum cardinality of any of the edges in the hypergraph. If all edges have the same cardinality k, the hypergraph is said to be uniform or k-uniform, or is called a k-hypergraph. A graph is just a 2-uniform hypergraph.The degree d(v) of a vertex v is the number of edges that contain it. H is k-regular if every vertex has degree k.
The dual of a uniform hypergraph is regular and vice-versa.
Two vertices x and y of H are called symmetric if there exists an automorphism such that
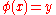. Two edges 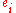and are said to be symmetric if there exists an automorphism such that 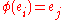.A hypergraph is said to be vertex-transitive (or vertex-symmetric) if all of its vertices are symmetric. Similarly, a hypergraph is edge-transitive if all edges are symmetric. If a hypergraph is both edge- and vertex-symmetric, then the hypergraph is simply transitive.
Because of hypergraph duality, the study of edge-transitivity is identical to the study of vertex-transitivity.
Transversals
A transversal or hitting set of a hypergraph H = (X, E) is a set that has nonempty intersectionIntersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
with every edge. A transversal T is called minimal if no proper subset of T is a transversal. The transversal hypergraph of H is the hypergraph (X, F) whose edge set F consists of all minimal transversals of H. Computing the transversal
Transversal
In geometry , when two coplanar lines exist such that a third coplanar line passes thru both lines. This third line is named the Transversal....
hypergraph has applications in machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
and other fields of computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, as game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, indexing of database
Index (database)
A database index is a data structure that improves the speed of data retrieval operations on a database table at the cost of slower writes and increased storage space...
s, SAT problem
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
, data mining
Data mining
Data mining , a relatively young and interdisciplinary field of computer science is the process of discovering new patterns from large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics and database systems...
and optimization
Optimization (computer science)
In computer science, program optimization or software optimization is the process of modifying a software system to make some aspect of it work more efficiently or use fewer resources...
.
Incidence matrix
Let and . Every hypergraph has an incidence matrixIncidence matrix
In mathematics, an incidence matrix is a matrix that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related ...
whereThe transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
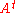of the incidenceIncidence (geometry)
In geometry, the relations of incidence are those such as 'lies on' between points and lines , and 'intersects' . That is, they are the binary relations describing how subsets meet...
matrix defines a hypergraph
called the dual of , where 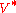is an m-element set and 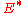is an n-element set of subsets of 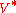. For and 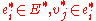if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
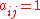.Hypergraph coloring
Hypergraph colouring is defined as follows. Let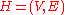 be a hypergraph such that . Then is a proper colouring of if and only if, for all 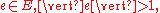there exists 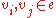such that 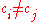.In other words: For every edge in the graph having at least two nodes as endpoints, the nodes this edge connects are not all of the same color.
Partitions
A partition theorem due to E. Dauber states that, for an edge-transitive hypergraph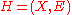, there exists a partitionPartition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
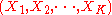
of the vertex set
such that the subhypergraph generated by is transitive for each , and such that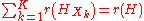where
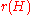is the rank of H.As a corollary, an edge-transitive hypergraph that is not vertex-transitive is bicolorable.
Graph partitioning (and in particular, hypergraph partitioning) has many applications to IC design and parallel computing.
Theorems
Many theoremTheorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s and concepts involving graphs also hold for hypergraphs. Ramsey's theorem
Ramsey's theorem
In combinatorics, Ramsey's theorem states that in any colouring of the edges of a sufficiently large complete graph, one will find monochromatic complete subgraphs...
and Line graph of a hypergraph are typical examples. Some methods for studying symmetries of graphs extend to hypergraphs.
Two prominent theorems are the Erdős–Ko–Rado theorem and the Kruskal–Katona theorem on uniform hypergraphs.
Hypergraph drawing
Although hypergraphs are more difficult to draw on paper than graphs, several researchers have studied methods for the visualization of hypergraphs.In one possible visual representation for hypergraphs, similar to the standard graph drawing
Graph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
style in which curves in the plane are used to depict graph edges, a hypergraph's vertices are depicted as points, disks, or boxes, and its hyperedges are depicted as trees that have the vertices as their leaves. If the vertices are represented as points, the hyperedges may also be shown as smooth curves that connect sets of points, or as simple closed curves that enclose sets of points.
In another style of hypergraph visualization, the subdivision model of hypergraph drawing, the plane is subdivided into regions, each of which represents a single vertex of the hypergraph. The hyperedges of the hypergraph are represented by contiguous subsets of these regions, which may be indicated by coloring, by drawing outlines around them, or both. An order-n Venn diagram
Venn diagram
Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...
, for instance, may be viewed as a subdivision drawing of a hypergraph with n hyperedges (the curves defining the diagram) and 2n − 1 vertices (represented by the regions into which these curves subdivide the plane). In contrast with the polynomial-time recognition of planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s, it is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
to determine whether a hypergraph has a planar subdivision drawing, but the existence of a drawing of this type may be tested efficiently when the adjacency pattern of the regions is constrained to be a path, cycle, or tree.
Generalizations
One possible generalization of a hypergraph is to allow edges to point at other edges. There are two variations of this generalization. In one, the edges consist not only of a set of vertices, but may also contain subsets of vertices, ad infinitum. Set membership then provides an ordering, but the ordering is neither a partial order nor a preorderPreorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
, since it is not transitive. The graph corresponding to the Levi graph of this generalization is a directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
. Consider, for example, the generalized hypergraph whose vertex set is
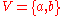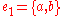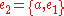and whose edges are and . Then, although 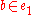and 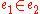, it is not true that . However, the transitive closureTransitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
of set membership for such hypergraphs does induce a partial order, and "flattens" the hypergraph into a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
.
Alternately, edges can be allowed to point at other edges, (irrespective of the requirement that the edges be ordered as directed, acyclic graphs). This allows graphs with edge-loops, which need not contain vertices at all. For example, consider the generalized hypergraph consisting of two edges
and , and 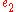zero vertices, so that 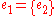and . As this loop is infinitely recursive, sets that are the edges violate the axiom of foundation. In particular, there is no transitive closure of set membership for such hypergraphs. Although such structures may seem strange at first, they can be readily understood by noting that the equivalent generalization of their Levi graph is no longer bipartiteBipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
, but is rather just some general directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
.
The generalized incidence matrix for such hypergraphs is, by definition, a square matrix, of a rank equal to the total number of vertices plus edges. Thus, for the above example, the incidence matrix
Incidence matrix
In mathematics, an incidence matrix is a matrix that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related ...
is simply
See also
- P systemP systemA P system is a computational model in the field of computer science that performs calculations using a biologically-inspired process. They are based upon the structure of biological cells, abstracting from the way in which chemicals interact and cross cell membranes...
- Factor graphFactor graphIn probability theory and its applications, a factor graph is a particular type of graphical model, with applications in Bayesian inference, that enables efficient computation of marginal distributions through the sum-product algorithm...
- GreedoidGreedoidIn combinatorics, a greedoid is a type of set system. It arises from the notion of the matroid, which was originally introduced by Whitney in 1935 to study planar graphs and was later used by Edmonds to characterize a class of optimization problems that can be solved by greedy algorithms...
- Incidence structureIncidence structureIn mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
- MatroidMatroidIn combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....