Set cover problem
Encyclopedia
The set covering problem (SCP) is a classical question in computer science
and complexity theory
.
It is a problem "whose study has led to the development of fundamental techniques for the entire field" of approximation algorithms. It was also one of Karp's 21 NP-complete problems
shown to be NP-complete
in 1972.
Given a set of elements (called the universe) and
(called the universe) and  sets whose union comprises the universe, the set cover problem is to identify the smallest number of sets whose union still contains all elements in the universe. For example, assume we are given the following elements
sets whose union comprises the universe, the set cover problem is to identify the smallest number of sets whose union still contains all elements in the universe. For example, assume we are given the following elements 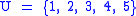 and sets
and sets 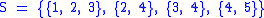 . Clearly the union of all the sets in
. Clearly the union of all the sets in 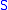 contain all elements in
contain all elements in  . However, we can cover all of the elements with the following, smaller number of sets:
. However, we can cover all of the elements with the following, smaller number of sets: 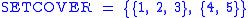 .
.
More formally, given a universe and a family
and a family 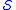 of subsets of
of subsets of  ,
,
a cover is a subfamily of sets whose union is
of sets whose union is  . In the set covering decision problem
. In the set covering decision problem
, the input is a pair and an integer
and an integer 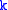 ; the question is whether
; the question is whether
there is a set covering of size or less. In the set covering optimization problem
or less. In the set covering optimization problem
, the input is a pair , and the task is to find a set covering that uses the fewest sets.
, and the task is to find a set covering that uses the fewest sets.
The decision version of set covering is NP-complete
, and the optimization version of set cover is NP-hard
.
This ILP belongs to the more general class of ILPs for covering problem
s.
The integrality gap of this ILP is at most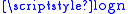 , so its relaxation gives a factor-
, so its relaxation gives a factor- approximation algorithm
approximation algorithm
for the minimum set cover problem (where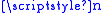 is the size of the universe).
is the size of the universe).
be viewed as an arbitrary bipartite graph
, with sets represented by vertices on the left, the universe represented by vertices on the
right, and edges representing the inclusion of elements in sets. The task is then to find a minimum cardinality subset of left-vertices which covers all of the right-vertices. In the Hitting set problem, the objective is to cover the left-vertices using a minimum subset of the right vertices. Converting from one problem to the other is therefore achieved by interchanging the two sets of vertices.
for set covering chooses sets according to one rule: at each stage, choose the set that contains the largest number of uncovered elements. It can be shown that this algorithm achieves an approximation ratio of , where
, where  is the size of the largest set and
is the size of the largest set and 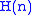 is the
is the  -th harmonic number:
-th harmonic number:

 There is a standard example on which the greedy algorithm achieves an approximation ratio of
There is a standard example on which the greedy algorithm achieves an approximation ratio of  .
.
The universe consists of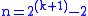 elements. The set system consists of
elements. The set system consists of 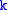 pairwise disjoint sets
pairwise disjoint sets
 with sizes
with sizes 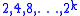 respectively, as well as two additional disjoint sets
respectively, as well as two additional disjoint sets 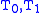 ,
,
each of which contains half of the elements from each . On this input, the greedy algorithm takes the sets
. On this input, the greedy algorithm takes the sets
 , in that order, while the optimal solution consists only of
, in that order, while the optimal solution consists only of 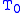 and
and 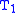 .
.
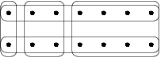
An example of such an input for is pictured on the right.
is pictured on the right.
Inapproximability results show that the greedy algorithm is essentially the best-possible polynomial time approximation algorithm for set cover
(see Inapproximability results below), under plausible complexity assumptions.
See k-approximation of k-hitting set
for an f-approximation of weighted set cover.
 , unless NP has quasi-polynomial time algorithms. Feige (1998)
, unless NP has quasi-polynomial time algorithms. Feige (1998)
improved this lower bound to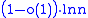 under the same assumptions, which essentially matches
under the same assumptions, which essentially matches
the approximation ratio achieved by the greedy algorithm. established a lower bound
of , where
, where  is a constant, under the weaker assumption that P
is a constant, under the weaker assumption that P NP.
NP.
A similar result with a higher value of was recently proved by .
was recently proved by .
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
.
It is a problem "whose study has led to the development of fundamental techniques for the entire field" of approximation algorithms. It was also one of Karp's 21 NP-complete problems
Karp's 21 NP-complete problems
One of the most important results in computational complexity theory was Stephen Cook's 1971 demonstration of the first NP-complete problem, the boolean satisfiability problem...
shown to be NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
in 1972.
Given a set of elements
 (called the universe) and
(called the universe) and  sets whose union comprises the universe, the set cover problem is to identify the smallest number of sets whose union still contains all elements in the universe. For example, assume we are given the following elements
sets whose union comprises the universe, the set cover problem is to identify the smallest number of sets whose union still contains all elements in the universe. For example, assume we are given the following elements 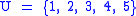 and sets
and sets 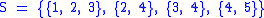 . Clearly the union of all the sets in
. Clearly the union of all the sets in 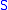 contain all elements in
contain all elements in  . However, we can cover all of the elements with the following, smaller number of sets:
. However, we can cover all of the elements with the following, smaller number of sets: 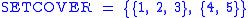 .
.More formally, given a universe
 and a family
and a family 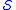 of subsets of
of subsets of  ,
,a cover is a subfamily
 of sets whose union is
of sets whose union is  . In the set covering decision problem
. In the set covering decision problemDecision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
, the input is a pair
 and an integer
and an integer 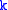 ; the question is whether
; the question is whetherthere is a set covering of size
 or less. In the set covering optimization problem
or less. In the set covering optimization problemOptimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
, the input is a pair
 , and the task is to find a set covering that uses the fewest sets.
, and the task is to find a set covering that uses the fewest sets.The decision version of set covering is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
, and the optimization version of set cover is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
.
Integer linear program formulation
The minimum set cover problem can be formulated as the following integer linear program.| minimize |  |
(minimize the total cost) | |
| subject to | 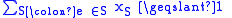 |
for all  |
(cover every element of the universe) |
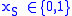 |
for all 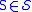 . . |
(every set is either in the set cover or not) |
This ILP belongs to the more general class of ILPs for covering problem
Covering problem
In combinatorics and computer science, covering problems are computational problems that ask whether a certain combinatorial structure 'covers' another, or how large the structure has to be to do that....
s.
The integrality gap of this ILP is at most
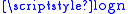 , so its relaxation gives a factor-
, so its relaxation gives a factor- approximation algorithm
approximation algorithmApproximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
for the minimum set cover problem (where
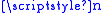 is the size of the universe).
is the size of the universe).Hitting set formulation
Set covering is equivalent to the Hitting set problem. It is easy to see this by observing that an instance of set covering canbe viewed as an arbitrary bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
, with sets represented by vertices on the left, the universe represented by vertices on the
right, and edges representing the inclusion of elements in sets. The task is then to find a minimum cardinality subset of left-vertices which covers all of the right-vertices. In the Hitting set problem, the objective is to cover the left-vertices using a minimum subset of the right vertices. Converting from one problem to the other is therefore achieved by interchanging the two sets of vertices.
Greedy algorithm
The greedy algorithmGreedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
for set covering chooses sets according to one rule: at each stage, choose the set that contains the largest number of uncovered elements. It can be shown that this algorithm achieves an approximation ratio of
 , where
, where  is the size of the largest set and
is the size of the largest set and 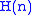 is the
is the  -th harmonic number:
-th harmonic number:

 .
.The universe consists of
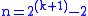 elements. The set system consists of
elements. The set system consists of 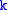 pairwise disjoint sets
pairwise disjoint sets with sizes
with sizes 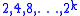 respectively, as well as two additional disjoint sets
respectively, as well as two additional disjoint sets 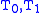 ,
,each of which contains half of the elements from each
 . On this input, the greedy algorithm takes the sets
. On this input, the greedy algorithm takes the sets , in that order, while the optimal solution consists only of
, in that order, while the optimal solution consists only of 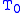 and
and 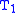 .
.An example of such an input for
 is pictured on the right.
is pictured on the right.Inapproximability results show that the greedy algorithm is essentially the best-possible polynomial time approximation algorithm for set cover
(see Inapproximability results below), under plausible complexity assumptions.
Low-frequency systems
If each element occurs in at most f sets, then a solution can be found in polynomial time that approximates the optimum to within a factor of f as follows: while an uncovered element exists, add all (at most f) sets which contain this element to the cover. In the end we end up with some cover, which we output. To see that this is an f-approximation it suffices to note that every time we add f sets, at least one of those is in an optimal cover as well. For f = 2, this is the normal approximation algorithm for vertex cover.See k-approximation of k-hitting set
K-approximation of k-hitting set
In computer science, k-approximation of k-hitting set is an approximation algorithm for weighted hitting set. The input is a collection S of subsets of some universe T and a mapping W from S to non-negative numbers called the weights of the elements of S. In k-hitting set the size of the sets in S...
for an f-approximation of weighted set cover.
Inapproximability results
showed that set covering cannot be approximated in polynomial time to within a factor of , unless NP has quasi-polynomial time algorithms. Feige (1998)
, unless NP has quasi-polynomial time algorithms. Feige (1998)improved this lower bound to
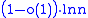 under the same assumptions, which essentially matches
under the same assumptions, which essentially matchesthe approximation ratio achieved by the greedy algorithm. established a lower bound
of
 , where
, where  is a constant, under the weaker assumption that P
is a constant, under the weaker assumption that P NP.
NP.A similar result with a higher value of
 was recently proved by .
was recently proved by .Related problems
- Hitting set is an equivalent reformulation of Set Cover.
- Vertex cover is a special case of Hitting Set.
- Edge cover is a special case of Set Cover.
- Set packingSet packingSet packing is a classical NP-complete problem in computational complexity theory and combinatorics, and was one of Karp's 21 NP-complete problems.Suppose we have a finite set S and a list of subsets of S...
is the dual problem of Set Cover. - Maximum coverage problemMaximum coverage problemThe maximum coverage problem is a classical question in computer science and computational complexity theory.It is a problem that is widely taught in approximation algorithms.As input you are given several sets and a number k....
is to choose at most k sets to cover as many elements as possible. - Dominating setDominating setIn graph theory, a dominating set for a graph G = is a subset D of V such that every vertex not in D is joined to at least one member of D by some edge...
is the problem of selecting a set of vertices (the dominating set) in a graph such that all other vertices are adjacent to at least one vertex in the dominating set. The Dominating set problem was shown NP complete by reducing it to Set cover

