In graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, an edge contraction is an operation

Graph operations

Operations on graphs produce new graphs from old ones. They may be separated into the following major categories.-Elementary operations:These are sometimes called "editing operations" on graphs...

 which removes an edge from a graph while simultaneously merging together the two vertices it previously connected. Edge contraction is a fundamental operation in the theory of graph minors

Minor (graph theory)

In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....

. Vertex identification is a less restrictive form of this operation.

Definition

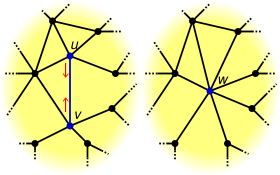
The edge contraction operation occurs relative to a particular edge, e. The edge e is removed and its two incident vertices, u and v, are merged into a new vertex w, where the edges incident to w each correspond to an edge incident to either u or v.

More generally, the operation may be performed on a set of edges by contracting each edge (in any order). Contractions may result in a graph with loops

Loop (graph theory)

In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....

 or multiple edges. These are sometimes deleted in order to keep within the class of simple graphs.

Formal definition

Let G=(V,E) be a graph (or directed graph

Directed graph

A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...

) containing an edge e=(u,v) with u≠v. Let f be a function which maps every vertex in V\{u,v} to itself, and otherwise, maps it to a new vertex w.
The contraction of e results in a new graph G′=(V′,E′), where V′=(V\{u,v})∪{w}, E′=E\{e}, and for every x∈V, x′=f(x)∈V′ is incident to an edge e′∈E′ if and only if, the corresponding edge, e∈E is incident to x in G.

Vertex identification

Vertex identification (sometimes called vertex contraction) removes the restriction that the contraction must occur over vertices sharing an incident edge. (Thus, edge contraction is a special case of vertex identification.) The operation may occur on any pair (or subset) of vertices in the graph. Edges between two contracting vertices are sometimes removed.

Path contraction

Path contraction occurs upon a the set of edges in a path

Path (graph theory)

In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...

 that contract to form a single edge between the endpoints of the path. Edges incident to vertices along the path are either eliminated, or arbitrarily (or systematically) connected to one of the endpoints.

Applications

Both edge and vertex contraction techniques are valuable in proof by induction on the number of vertices or edges in a graph, where it can be assumed that a property holds for all smaller graphs and this can be used to prove the property for the larger graph.

Contractions are also useful in structures where we wish to simplify a graph by identifying vertices that represent essentially equivalent entities. One of the most common examples is the reduction of a general directed graph

Directed graph

A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...

 to an acyclic directed graph by contracting all of the vertices in each strongly connected component

Strongly connected component

A directed graph is called strongly connected if there is a path from each vertex in the graph to every other vertex. In particular, this means paths in each direction; a path from a to b and also a path from b to a....

. If the relation described by the graph is transitive

Transitive relation

In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....

, no information is lost as long as we label each vertex with the set of labels of the vertices that were contracted to form it.

Another example is the coalescing performed in global graph coloring register allocation, where vertices are contracted (where it is safe) in order to eliminate move operations between distinct variables.

Edge contraction is used in 3D modelling packages (either manually, or through some feature of the modelling software) to consistently reduce vertex count, aiding in the creation of low-polygon models.

External links

• Mathworld: Edge Contraction