A directed graph

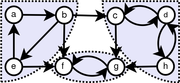
Directed graph

A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...

 is called strongly connected if there is a path

Path (graph theory)

In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...

 from each vertex

Vertex (graph theory)

In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...

 in the graph to every other vertex. In particular, this means paths in each direction; a path from a to b and also a path from b to a.

The strongly connected components of a directed graph

Directed graph

A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...

 G are its maximal strongly connected subgraphs. If each strongly connected component is contracted to a single vertex, the resulting graph is a directed acyclic graph

Directed acyclic graph

In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...

, the condensation of G. A directed graph is acyclic if and only if it has no (nontrivial) strongly connected subgraphs (because a cycle is strongly connected, and every strongly connected graph contains at least one cycle).

Kosaraju's algorithm

Kosaraju's algorithm

In computer science, the Kosaraju-Sharir algorithm is an algorithm to find the strongly connected components of a directed graph. Aho, Hopcroft and Ullman credit it to an unpublished paper from 1978 by S. Rao Kosaraju and Micha Sharir...

, Tarjan's algorithm

Tarjan's strongly connected components algorithm

Tarjan's Algorithm is a graph theory algorithm for finding the strongly connected components of a graph...

 and Gabow's algorithm all efficiently compute the strongly connected components of a directed graph, but Tarjan's and Gabow's are favoured in practice since they require only one depth-first search

Depth-first search

Depth-first search is an algorithm for traversing or searching a tree, tree structure, or graph. One starts at the root and explores as far as possible along each branch before backtracking....

 rather than two.

Algorithms for finding strongly connected components may be used to solve 2-satisfiability

2-satisfiability

In computer science, 2-satisfiability is the problem of determining whether a collection of two-valued variables with constraints on pairs of variables can be assigned values satisfying all the constraints...

 problems (systems of Boolean variables with constraints on the values of pairs of variables): as showed, a 2-satisfiability

2-satisfiability

In computer science, 2-satisfiability is the problem of determining whether a collection of two-valued variables with constraints on pairs of variables can be assigned values satisfying all the constraints...

 instance is unsatisfiable if and only if there is a variable v such that v and its complement are both contained in the same strongly connected component of the implication graph

Implication graph

In mathematical logic, an implication graph is a skew-symmetric directed graph G composed of vertex set V and directed edge set E. Each vertex in V represents the truth status of a Boolean literal, and each directed edge from vertex u to vertex v represents the material implication "If the literal...

 of the instance.

According to Robbins theorem

Robbins theorem

In graph theory, a strong orientation of an undirected graph is an assignment of a direction to each edge that makes it into a strongly connected graph. Robbins' theorem, named after , states that the graphs that have strong orientations are exactly the 2-edge-connected graphs...

, an undirected graph may be oriented in such a way that it becomes strongly connected, if and only if it is 2-edge-connected

K-edge-connected graph

In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G =  be an arbitrary graph....

.