2-satisfiability
Encyclopedia
In computer science
, 2-satisfiability (abbreviated as 2-SAT or just 2SAT) is the problem of determining whether a collection of two-valued (Boolean
or binary
) variables with constraints
on pairs of variables can be assigned values satisfying all the constraints. It is a special case of the general Boolean satisfiability problem
, which can involve constraints on more than two variables, and of constraint satisfaction problem
s, which can allow more than two choices for the value of each variable. But in contrast to those problems, which are NP-complete
, it has a known polynomial time solution. Instances of the 2-satisfiability problem are typically expressed as 2-CNF
or Krom formulas.
A 2-SAT problem may be described using a Boolean expression
with a special restricted form: a conjunction
of disjunctions (and of ors), where each disjunction (or operation) has two arguments that may either be variables or the negations of variables. The variables or their negations appearing in this formula are known as terms
and the disjunctions of pairs of terms are known as clauses
. For example, the following formula is in conjunctive normal form, with seven variables and eleven clauses:
The 2-satisfiability problem is to find a truth assignment to these variables that makes a formula of this type true: we must choose whether to make each of the variables true or false, so that every clause has at least one term that becomes true. For the expression shown above, one possible satisfying assignment is the one that sets all seven of the variables to true. There are also 15 other ways of setting all the variables so that the formula becomes true. Therefore, the 2-SAT instance represented by this expression is satisfiable.
Formulas with the form described above are known as 2-CNF formulas; the "2" in this name stands for the number of terms per clause, and "CNF" stands for conjunctive normal form
, a type of Boolean expression in the form of a conjunction of disjunctions. They are also called Krom formulas, after the work of UC Davis
mathematician Melven R. Krom, whose 1967 paper was one of the earliest works on the 2-satisfiability problem.
Each clause in a 2-CNF formula is logically equivalent
to an implication from one variable or negated variable to the other. For example,
Because of this equivalence between these different types of operation, a 2-satisfiability instance may also be written in implicative normal form, in which we replace each or operation in the conjunctive normal form by both of the two implications to which it is equivalent.
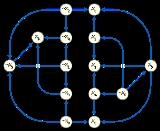
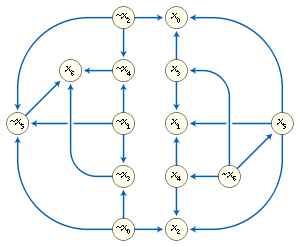
A third, more graphical way of describing a 2-satisfiability instance is as an implication graph
. An implication graph is a directed graph
in which there is one vertex
per variable or negated variable, and an edge connecting one vertex to another whenever the corresponding variables are related by an implication in the implicative normal form of the instance. An implication graph must be a skew-symmetric graph
, meaning that the undirected graph formed by forgetting the orientations of its edges has a symmetry
that takes each variable to its negation and reverses the orientations of all of the edges.
Suppose that a 2-satisfiability instance contains two clauses that both use the same variable x, but that x is negated in one clause and not in the other. Then we may combine the two clauses to produce a third clause, having the two other terms in the two clauses; this third clause must also be satisfied whenever the first two clauses are both satisfied. For instance, we may combine the clauses
and 
in this way to produce the clause 
. In terms of the implicative form of a 2-CNF formula, this rule amounts to finding two implications 
and 
, and inferring by transitivity
a third implication
.
Krom writes that a formula is consistent if repeated application of this inference rule cannot generate both the clauses
and 
, for any variable 
. As he proves, a 2-CNF formula is satisfiable if and only if it is consistent. For, if a formula is not consistent, it is not possible to satisfy both of the two clauses 
and 
simultaneously. And, if it is consistent, then the formula can be extended by repeatedly adding one clause of the form 
or 
at a time, preserving consistency at each step, until it includes such a clause for every variable. At each of these extension steps, one of these two clauses may always be added while preserving consistency, for if not then the other clause could be generated using the inference rule. Once all variables have a clause of this form in the formula, a satisfying assignment of all of the variables may be generated by setting a variable 
to true if the formula contains the clause 
and setting it to false if the formula contains the clause 
. If there were a clause not satisfied by this assignment, i.e., one in which both variables appeared with sign opposite to their appearances in the added clauses, it would be possible to resolve this clause with one to reverse the sign of that variable, and then to resolve it with the original clause to produce a clause of the other variable in double with the sign it held in the original clause. Since the formula is known to have remained consistent, this is impossible, so the assignment must satisfy the original formula as well.
Krom was concerned primarily with completeness
of systems of inference rules, rather than with the efficiency of algorithms. However, his method leads to a polynomial time bound for solving 2-satisfiability problems.
By grouping together all of the clauses that use the same variable, and applying the inference rule to each pair of clauses, it is possible to find all inferences that are possible from a given 2-CNF instance, and to test whether it is consistent, in total time , where is the number of variables in the instance: for each variable, there may be pairs of clauses involving that variable, to which the inference rule may be applied. Thus, it is possible to determine whether a given 2-CNF instance is satisfiable in time . Because finding a satisfying assignment using Krom's method involves a sequence of consistency checks, it would take time . quote a faster time bound of for this algorithm, based on more careful ordering of its operations. Nevertheless, even this smaller time bound was greatly improved by the later linear time algorithms of and .
In terms of the implication graph of the 2-satisfiability instance, Krom's inference rule can be interpreted as constructing the transitive closure
of the graph. As observes, it can also be seen as an instance of the Davis–Putnam algorithm
for solving satisfiability problems using the principle of resolution
. Its correctness follows from the more general correctness of the Davis-Putnam algorithm, and its polynomial time bound is clear since each resolution step increases the number of clauses in the instance, which is upper bounded by a quadratic function of the number of variables.
for solving constraint satisfaction problems with binary variables and pairwise constraints; they apply this technique to a problem of classroom scheduling, but they also observe that it applies to other problems including 2-SAT.
The basic idea of their approach is to build a partial truth assignment, one variable at a time. Certain steps of the algorithms are "choice points", points at which a variable can be given either of two different truth values, and later steps in the algorithm may cause it to backtrack to one of these choice points. However, only the most recent choice can be backtracked over; all choices made earlier than the most recent one are permanent.
Initially, there is no choice point, and all variables are unassigned.
At each step, the algorithm chooses the variable whose value to set, as follows:
Intuitively, the algorithm follows all chains of inference after making each of its choices; this either leads to a contradiction and a backtracking step, or, if no contradiction is derived, it follows that the choice was a correct one that leads to a satisfying assignment. Therefore, the algorithm either correctly finds a satisfying assignment or it correctly determines that the input is unsatisfiable.
Even et al. did not describe in detail how to implement this algorithm efficiently; they state only that by "using appropriate data structures in order to find the implications of any decision", each step of the algorithm (other than the backtracking) can be performed quickly. However, some inputs may cause the algorithm to backtrack many times, each time performing many steps before backtracking, so its overall complexity may be nonlinear. To avoid this problem, they modify the algorithm so that, after reaching each choice point, it tests in parallel both alternative assignments for the variable set at the choice point, interleaving both parallel tests to produce a sequential algorithm. As soon as one of these two parallel tests reaches another choice point, the other parallel branch is aborted. In this way, the total time spent performing both parallel tests is proportional to the size of the portion of the input formula whose values are permanently assigned. As a result, the algorithm takes linear time in total.
s from graph theory
.
Two vertices in a directed graph are said to be strongly connected to each other if there is a directed path from one to the other and vice versa. This is an equivalence relation
, and the vertices of the graph may be partitioned into strongly connected components, subsets within which every two vertices are strongly connected. There are several efficient linear time algorithms for finding the strongly connected components of a graph, based on depth first search: Tarjan's strongly connected components algorithm
and Gabow's algorithm
each perform a single depth first search. Kosaraju's algorithm
performs two depth first searches, but is very simple: the first search is used only to order the vertices, in the reverse of a postorder depth-first traversal. Then, the second pass of the algorithm loops through the vertices in this order, and for each vertex that has not already been assigned to a component, it performs a depth-first search of the transpose graph
starting from that vertex, backtracking when the search reaches a previously-assigned vertices; the unsassigned vertices reached by this search form a new component.
In terms of the implication graph, two terms belong to the same strongly connected component whenever there exist chains of implications from one term to the other and vice versa. Therefore, the two terms must have the same value in any satisfying assignment to the given 2-satisfiability instance. In particular, if a variable and its negation both belong to the same strongly connected component, the instance cannot be satisfied, because it is impossible to assign both of these terms the same value. As Aspvall et al. showed, this is a necessary and sufficient condition: a 2-CNF formula is satisfiable if and only if there is no variable that belongs to the same strongly connected component as its negation.
This immediately leads to a linear time algorithm for testing satisfiability of 2-CNF formulae: simply perform a strong connectivity analysis on the implication graph and check that each variable and its negation belong to different components. However, as Aspvall et al. also showed, it also leads to a linear time algorithm for finding a satisfying assignment, when one exists. Their algorithm performs the following steps:
Due to the topological ordering, when a term is set to false, all terms that lead to it via a chain of implications will themselves already have been set to false. Symmetrically, when a term is set to true, all terms that can be reached from it via a chain of implications will already have been set to true. Therefore, the truth assignment constructed by this procedure satisfies the given formula, which also completes the proof of correctness of the necessary and sufficient condition identified by Aspvall et al.
As Aspvall et al. show, a similar procedure involving topologically ordering the strongly connected components of the implication graph may also be used to evaluate fully quantified Boolean formulae
in which the formula being quantified is a 2-CNF formula.
problem are based on 2-satisfiability. This problem concerns placing textual labels on the features of a diagram or map. Typically, the set of possible locations for each label is highly constrained, not only by the map itself (each label must be near the feature it labels, and must not obscure other features), but by each other: two labels will be illegible if they overlap each other. In general, label placement is an NP-hard
problem. However, if each feature has only two possible locations for its label (say, extending to the left and to the right of the feature) then it may be solved in polynomial time. For, in this case, one may create a 2-satisfiability instance that has a variable for each label and constraints preventing each pair of labels from being assigned overlapping positions. If the labels are all congruent rectangles, the corresponding 2-SAT instance can be shown to have only linearly many constraints, leading to near-linear time algorithms for finding a labeling. describe a map labeling problem in which each label is a rectangle that may be placed in one of three positions with respect to a line segment that it labels: it may have the segment as one of its sides, or it may be centered on the segment. They represent these three positions using two binary variables in such a way that, again, testing the existence of a valid labeling becomes a 2-SAT problem.
use this observation as part of an approximation algorithm
for the problem of finding square labels of the largest possible size for a given set of points, with the constraint that each label has one of its corners on the point that it labels. To find a labeling with a given size, they eliminate squares that, if doubled, would overlap another points, and they eliminate points that can be labeled in a way that cannot possibly overlap with another point's label, and they show that the remaining points have only two possible label placements, allowing the 2-SAT approach to be used. By searching for the largest size that leads to a solvable 2-SAT instance, they find a solution with approximation ratio at most two. Similarly, if each label is rectangular and must be placed in such a way that the point it labels is somewhere along its bottom edge, then using 2-SAT to find the optimal solution in which the label has the point on a bottom corner leads to an approximation ratio of at most two.
Similar reductions to 2-satisfiability have been applied to other geometric placement problems. In graph drawing
, if the vertex locations are fixed and each edge must be drawn as a circular arc with one of two possible locations, then the problem of choosing which arc to use for each edge in order to avoid crossings is a 2SAT problem with a variable for each edge and a constraint for each pair of placements that would lead to a crossing. However, in this case it is possible to speed up the solution, compared to an algorithm that builds and then searches an explicit representation of the implication graph, by searching the graph implicitly
.
In VLSI integrated circuit design, if a collection of modules must be connected by wires that can each bend at most once, then again there are two possible routes for the wires, and the problem of choosing which of these two routes to use, in such a way that all wires can be routed in a single layer of the circuit, can be solved as a 2SAT instance.
consider another VLSI design problem: the question of whether or not to mirror-reverse each module in a circuit design. This mirror reversal leaves the module's operations unchanged, but it changes the order of the points at which the input and output signals of the module connect to it, possibly changing how well the module fits into the rest of the design. Boros et al. consider a simplified version of the problem in which the modules have already been placed along a single linear channel, in which the wires between modules must be routed, and there is a fixed bound on the density of the channel (the maximum number of signals that must pass through any cross-section of the channel). They observe that this version of the problem may be solved as a 2-SAT instance, in which the constraints relate the orientations of pairs of modules that are directly across the channel from each other; as a consequence, the optimal density may also be calculated efficiently, by performing a binary search in which each step involves the solution of a 2-SAT instance.
in a metric space
into two clusters is to choose the clusters in such a way as to minimize the sum of the diameter
s of the clusters, where the diameter of any single cluster is the largest distance between any two of its points; this is preferable to minimizing the maximum cluster size, which may lead to very similar points being assigned to different clusters. If the target diameters of the two clusters are known, a clustering that achieves those targets may be found by solving a 2-satisfiability instance. The instance has one variable per point, indicating whether that point belongs to the first cluster or the second cluster. Whenever any two points are too far apart from each other for both to belong to the same cluster, a clause is added to the instance that prevents this assignment.
The same method also can be used as a subroutine when the individual cluster diameters are unknown. To test whether a given sum of diameters can be achieved without knowing the individual cluster diameters, one may try all maximal pairs of target diameters that add up to at most the given sum, representing each pair of diameters as a 2-satisfiability instance and using a 2-satisfiability algorithm to determine whether that pair can be realized by a clustering. To find the optimal sum of diameters one may perform a binary search in which each step is a feasibility test of this type. The same approach also works to find clusterings that optimize other combinations than sums of the cluster diameters, and that use arbitrary dissimilarity numbers (rather than distances in a metric space) to measure the size of a cluster. The time bound for this algorithm is dominated by the time to solve a sequence of 2-SAT instances that are closely related to each other, and shows how to solve these related instances more quickly than if they were solved independently from each other, leading to a total time bound of for the sum-of-diameters clustering problem.
, even when each teacher has at most three available hours, but it can be solved as an instance of 2-satisfiability when each teacher only has two available hours. (Teachers with only a single available hour may easily be eliminated from the problem.) In this problem, each variable vij corresponds to an hour that teacher i must spend with cohort j, the assignment to the variable specifies whether that hour is the first or the second of the teacher's available hours, and there is a 2-SAT clause preventing any conflict of either of two types: two cohorts assigned to a teacher at the same time as each other, or one cohort assigned to two teachers at the same time.
apply 2-satisfiability to a problem of sports scheduling, in which the pairings of a round-robin tournament
have already been chosen and the games must be assigned to the teams' stadiums. In this problem, it is desirable to alternate home and away games to the extent possible, avoiding "breaks" in which a team plays two home games in a row or two away games in a row. At most two teams can avoid breaks entirely, alternating between home and away games; no other team can have the same home-away schedule as these two, because then it would be unable to play the team with which it had the same schedule. Therefore, an optimal schedule has two breakless teams and a single break for every other team. Once one of the breakless teams is chosen, one can set up a 2-satisfiability problem in which each variable represents the home-away assignment for a single team in a single game, and the constraints enforce the properties that any two teams have a consistent assignment for their games, that each team have at most one break before and at most one break after the game with the breakless team, and that no team has two breaks. Therefore, testing whether a schedule admits a solution with the optimal number of breaks can be done by solving a linear number of 2-satisfiability problems, one for each choice of the breakless team. A similar technique also allows finding schedules in which every team has a single break, and maximizing rather than minimizing the number of breaks (to reduce the total mileage traveled by the teams).
is the process of recovering shapes from their cross-sections.
In digital tomography, a simplified version of the problem that has been frequently studied, the shape to be recovered is a polyomino
(a subset of the squares in the two-dimensional square lattice
), and the cross-sections provide aggregate information about the sets of squares in individual rows and columns of the lattice. For instance, in the popular nonogram puzzles, also known as paint by numbers or griddlers, the set of squares to be determined represents the dark pixel
s in a bitmap image
, and the input given to the puzzle solver tells him or her how many consecutive blocks of dark pixels to include in each row or column of the image, and how long each of those blocks should be. In other forms of digital tomography, even less information about each row or column is given: only the total number of squares, rather than the number and length of the blocks of squares. An equivalent version of the problem is that we must recover a given 0-1 matrix given only the sums of the values in each row and in each column of the matrix.
Although there exist polynomial time algorithms to find a matrix having given row and column sums, the solution may be far from unique: any submatrix in the form of a 2 × 2 identity matrix
can be complemented without affecting the correctness of the solution. Therefore, researchers have searched for constraints on the shape to be reconstructed that can be used to restrict the space of solutions. For instance, one might assume that the shape is connected; however, testing whether there exists a connected solution is NP-complete. An even more constrained version that is easier to solve is that the shape is orthogonally convex: having a single contiguous block of squares in each row and column.
Improving several previous solutions, showed how to reconstruct connected orthogonally convex shapes efficiently, using 2-SAT. The idea of their solution is to guess the indexes of rows containing the leftmost and rightmost cells of the shape to be reconstructed, and then to set up a 2-SAT problem that tests whether there exists a shape consistent with these guesses and with the given row and column sums. They use four 2-SAT variables for each square that might be part of the given shape, one to indicate whether it belongs to each of four possible "corner regions" of the shape, and they use constraints that force these regions to be disjoint, to have the desired shapes, to form an overall shape with contiguous rows and columns, and to have the desired row and column sums. Their algorithm takes time where is the smaller of the two dimensions of the input shape and is the larger of the two dimensions. The same method was later extended to orthogonally convex shapes
that might be connected only diagonally instead of requiring orthogonal connectivity.
More recently, as part of a solver for full nonogram puzzles, used 2-SAT to combine information obtained from several other heuristic
s. Given a partial solution to the puzzle, they use dynamic programming
within each row or column to determine whether the constraints of that row or column force any of its squares to be white or black, and whether any two squares in the same row or column can be connected by an implication relation. They also transform the nonogram into a digital tomography problem by replacing the sequence of block lengths in each row and column by its sum, and use a maximum flow formulation to determine whether this digital tomography problem combining all of the rows and columns has any squares whose state can be determined or pairs of squares that can be connected by an implication relation. If either of these two heuristics determines the value of one of the squares, it is included in the partial solution and the same calculations are repeated. However, if both heuristics fail to set any squares, the implications found by both of them are combined into a 2-satisfiability problem and a 2-satisfiability solver is used to find squares whose value is fixed by the problem, after which the procedure is again repeated. This procedure may or may not succeed in finding a solution, but it is guaranteed to run in polynomial time. Batenburg and Kosters report that, although most newspaper puzzles do not need its full power, both this procedure and a more powerful but slower procedure which combines this 2-SAT approach with the limited backtracking of are significantly more effective than the dynamic programming and flow heuristics without 2-SAT when applied to more difficult randomly generated nonograms.
and a small number of complete bipartite subgraphs
, inferring business relationships among autonomous subsystems of the internet, and reconstruction of evolutionary trees.
ic amount of writable memory, is easy to describe: simply choose (nondeterministically) a variable v and search (nondeterministically) for a chain of implications leading from v to its negation and then back to v. If such a chain is found, the instance cannot be satisfiable. By the Immerman-Szelepcsényi theorem
, it is also possible in nondeterministic logspace to verify that a satisfiable 2-SAT instance is satisfiable.
2-satisfiability is NL-complete
, meaning that it is one of the "hardest" or "most expressive" problems in the complexity class
NL
of problems solvable nondeterministically in logarithmic space. Completeness here means that a deterministic Turing machine using only logarithmic space can transform any other problem in NL into an equivalent 2-satisfiability problem. Analogously to similar results for the more well-known complexity class NP
, this transformation together with the Immerman-Szelepcsényi theorem allow any problem in NL to be represented as a second order logic formula with a single existentially quantified predicate with clauses limited to length 2; such formulae are known as SO-Krom. Similarly, the implicative normal form can be expressed in first order logic with the addition of an operator for transitive closure
.
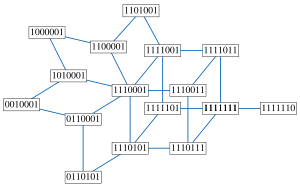The set of all solutions to a 2-satisfiability instance has the structure of a median graph
, in which an edge corresponds to the operation of flipping the values of a set of variables that are all constrained to be equal or unequal to each other. In particular, by following edges in this way one can get from any solution to any other solution. Conversely, any median graph can be represented as the set of solutions to a 2-satisfiability instance in this way. The median of any three solutions is formed by setting each variable to the value it holds in the majority
of the three solutions; this median always forms another solution to the instance.
describes an algorithm for efficiently listing all solutions to a given 2-satisfiability instance, and for solving several related problems.
There also exist algorithms for finding two satisfying assignments that have the maximal Hamming distance
from each other.
is #P-complete, which implies that it is not solvable in polynomial time unless P = NP. Moreover, there is no fully polynomial randomized approximation scheme
for #2SAT unless NP
= RP
and this even holds when the input is restricted to monotone 2-CNF formulas, i.e., 2-CNF formulas in which each literal
is a positive occurrence of a variable.
The fastest known algorithm for computing the exact number of satisfying assignments to a 2SAT formula runs in time
.
as n goes to infinity: if α < 1, the limit is one, while if α > 1, the limit is zero. Thus, the problem exhibits a phase transition
at α = 1.
with two literals
per clause, and the task is to determine the maximum number of clauses that can be simultaneously satisfied by an assignment. MAX-2-SAT is NP-hard
and it is a particular case of a maximum satisfiability problem
.
By formulating MAX-2-SAT as a problem of finding a cut
(that is, a partition of the vertices into two subsets) maximizing the number of edges that have one endpoint in the first subset and one endpoint in the second, in a graph related to the implication graph, and applying semidefinite programming
methods to this cut problem, it is possible to find in polynomial time an approximate solution that satisfies at least 0.940... times the optimal number of clauses. A balanced MAX 2-SAT instance is an instance of MAX 2-SAT where every variable appears positively and negatively with equal weight. For this problem, one can improve the approximation ratio to
.
If the unique games conjecture
is true, then it is impossible to approximate MAX 2-SAT, balanced or not, with an approximation constant better than 0.943... in polynomial time.
Under the weaker assumption that P ≠ NP, the problem is only known to be inapproximable within a constant better than 21/22 = 0.95454...
Various authors have also explored exponential worst-case time bounds for exact solution of MAX-2-SAT instances.
-variable 2SAT instance and an integer , and the problem is to decide whether there exists a satisfying assignment in which at most of the variables are true. One may easily encode the vertex cover problem as a W2SAT problem: given a graph and a bound on the size of a vertex cover, create a variable for each vertex of a graph, and for each edge of the graph create a 2SAT clause . Then the satisfying instances of the resulting 2SAT formula encode solutions to the vertex cover problem, and there is a satisfying assignment with true variables if and only if there is a vertex cover with vertices. Therefore, W2SAT is NP-complete
.
Moreover, in parameterized complexity
W2SAT provides a natural W[1]-complete problem, which implies that W2SAT is not fixed-parameter tractable unless this holds for all problems in W[1]. That is, it is unlikely that there exists an algorithm for W2SAT whose running time takes the form . Even more strongly, W2SAT cannot be solved in time unless the exponential time hypothesis
fails.
in which the formula being quantified is a 2-CNF formula. The 2-satisfiability problem is the special case of this quantified 2-CNF problem, in which all quantifiers are existential. Krom also developed an effective decision procedure for these formulae; showed that it can be solved in linear time, by an extension of their technique of strongly connected components and topological ordering.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, 2-satisfiability (abbreviated as 2-SAT or just 2SAT) is the problem of determining whether a collection of two-valued (Boolean
Boolean logic
Boolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...
or binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
) variables with constraints
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
on pairs of variables can be assigned values satisfying all the constraints. It is a special case of the general Boolean satisfiability problem
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
, which can involve constraints on more than two variables, and of constraint satisfaction problem
Constraint satisfaction problem
Constraint satisfaction problems s are mathematical problems defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variables, which is solved by constraint...
s, which can allow more than two choices for the value of each variable. But in contrast to those problems, which are NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
, it has a known polynomial time solution. Instances of the 2-satisfiability problem are typically expressed as 2-CNF
Conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
or Krom formulas.
Problem representations
Boolean expression
In computer science, a Boolean expression is an expression in a programming language that produces a Boolean value when evaluated, i.e. one of true or false...
with a special restricted form: a conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
of disjunctions (and of ors), where each disjunction (or operation) has two arguments that may either be variables or the negations of variables. The variables or their negations appearing in this formula are known as terms
Term (logic)
In mathematical logic, universal algebra, and rewriting systems, terms are expressions which can be obtained from constant symbols, variables and function symbols...
and the disjunctions of pairs of terms are known as clauses
Clause (logic)
In logic, a clause is a finite disjunction ofliterals. Clausesare usually written as follows, where the symbols l_i areliterals:l_1 \vee \cdots \vee l_nIn some cases, clauses are written as sets of literals, so that clause above...
. For example, the following formula is in conjunctive normal form, with seven variables and eleven clauses:
The 2-satisfiability problem is to find a truth assignment to these variables that makes a formula of this type true: we must choose whether to make each of the variables true or false, so that every clause has at least one term that becomes true. For the expression shown above, one possible satisfying assignment is the one that sets all seven of the variables to true. There are also 15 other ways of setting all the variables so that the formula becomes true. Therefore, the 2-SAT instance represented by this expression is satisfiable.
Formulas with the form described above are known as 2-CNF formulas; the "2" in this name stands for the number of terms per clause, and "CNF" stands for conjunctive normal form
Conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
, a type of Boolean expression in the form of a conjunction of disjunctions. They are also called Krom formulas, after the work of UC Davis
University of California, Davis
The University of California, Davis is a public teaching and research university established in 1905 and located in Davis, California, USA. Spanning over , the campus is the largest within the University of California system and third largest by enrollment...
mathematician Melven R. Krom, whose 1967 paper was one of the earliest works on the 2-satisfiability problem.
Each clause in a 2-CNF formula is logically equivalent
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
to an implication from one variable or negated variable to the other. For example,
Because of this equivalence between these different types of operation, a 2-satisfiability instance may also be written in implicative normal form, in which we replace each or operation in the conjunctive normal form by both of the two implications to which it is equivalent.
A third, more graphical way of describing a 2-satisfiability instance is as an implication graph
Implication graph
In mathematical logic, an implication graph is a skew-symmetric directed graph G composed of vertex set V and directed edge set E. Each vertex in V represents the truth status of a Boolean literal, and each directed edge from vertex u to vertex v represents the material implication "If the literal...
. An implication graph is a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
in which there is one vertex
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
per variable or negated variable, and an edge connecting one vertex to another whenever the corresponding variables are related by an implication in the implicative normal form of the instance. An implication graph must be a skew-symmetric graph
Skew-symmetric graph
In graph theory, a branch of mathematics, a skew-symmetric graph is a directed graph that is isomorphic to its own transpose graph, the graph formed by reversing all of its edges. The isomorphism is required to be an involution without any fixed points....
, meaning that the undirected graph formed by forgetting the orientations of its edges has a symmetry
Graph automorphism
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....
that takes each variable to its negation and reverses the orientations of all of the edges.
Algorithms
Several algorithms are known for solving the 2-satisfiability problem; the most efficient of them take linear time.Resolution and transitive closure
described the following polynomial time decision procedure for solving 2-satisfiability instances.Suppose that a 2-satisfiability instance contains two clauses that both use the same variable x, but that x is negated in one clause and not in the other. Then we may combine the two clauses to produce a third clause, having the two other terms in the two clauses; this third clause must also be satisfied whenever the first two clauses are both satisfied. For instance, we may combine the clauses
and in this way to produce the clause . In terms of the implicative form of a 2-CNF formula, this rule amounts to finding two implications and , and inferring by transitivityTransitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
a third implication
.Krom writes that a formula is consistent if repeated application of this inference rule cannot generate both the clauses
and , for any variable . As he proves, a 2-CNF formula is satisfiable if and only if it is consistent. For, if a formula is not consistent, it is not possible to satisfy both of the two clauses and simultaneously. And, if it is consistent, then the formula can be extended by repeatedly adding one clause of the form or at a time, preserving consistency at each step, until it includes such a clause for every variable. At each of these extension steps, one of these two clauses may always be added while preserving consistency, for if not then the other clause could be generated using the inference rule. Once all variables have a clause of this form in the formula, a satisfying assignment of all of the variables may be generated by setting a variable to true if the formula contains the clause and setting it to false if the formula contains the clause . If there were a clause not satisfied by this assignment, i.e., one in which both variables appeared with sign opposite to their appearances in the added clauses, it would be possible to resolve this clause with one to reverse the sign of that variable, and then to resolve it with the original clause to produce a clause of the other variable in double with the sign it held in the original clause. Since the formula is known to have remained consistent, this is impossible, so the assignment must satisfy the original formula as well.Krom was concerned primarily with completeness
Completeness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
of systems of inference rules, rather than with the efficiency of algorithms. However, his method leads to a polynomial time bound for solving 2-satisfiability problems.
By grouping together all of the clauses that use the same variable, and applying the inference rule to each pair of clauses, it is possible to find all inferences that are possible from a given 2-CNF instance, and to test whether it is consistent, in total time , where is the number of variables in the instance: for each variable, there may be pairs of clauses involving that variable, to which the inference rule may be applied. Thus, it is possible to determine whether a given 2-CNF instance is satisfiable in time . Because finding a satisfying assignment using Krom's method involves a sequence of consistency checks, it would take time . quote a faster time bound of for this algorithm, based on more careful ordering of its operations. Nevertheless, even this smaller time bound was greatly improved by the later linear time algorithms of and .
In terms of the implication graph of the 2-satisfiability instance, Krom's inference rule can be interpreted as constructing the transitive closure
Transitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
of the graph. As observes, it can also be seen as an instance of the Davis–Putnam algorithm
Davis–Putnam algorithm
The Davis–Putnam algorithm was developed by Martin Davis and Hilary Putnam for checking the validity of a first-order logic formula using a resolution-based decision procedure for propositional logic. Since the set of valid first-order formulas is recursively enumerable but not recursive, there...
for solving satisfiability problems using the principle of resolution
Resolution (logic)
In mathematical logic and automated theorem proving, resolution is a rule of inference leading to a refutation theorem-proving technique for sentences in propositional logic and first-order logic...
. Its correctness follows from the more general correctness of the Davis-Putnam algorithm, and its polynomial time bound is clear since each resolution step increases the number of clauses in the instance, which is upper bounded by a quadratic function of the number of variables.
Limited backtracking
describe a technique involving limited backtrackingBacktracking
Backtracking is a general algorithm for finding all solutions to some computational problem, that incrementally builds candidates to the solutions, and abandons each partial candidate c as soon as it determines that c cannot possibly be completed to a valid solution.The classic textbook example...
for solving constraint satisfaction problems with binary variables and pairwise constraints; they apply this technique to a problem of classroom scheduling, but they also observe that it applies to other problems including 2-SAT.
The basic idea of their approach is to build a partial truth assignment, one variable at a time. Certain steps of the algorithms are "choice points", points at which a variable can be given either of two different truth values, and later steps in the algorithm may cause it to backtrack to one of these choice points. However, only the most recent choice can be backtracked over; all choices made earlier than the most recent one are permanent.
Initially, there is no choice point, and all variables are unassigned.
At each step, the algorithm chooses the variable whose value to set, as follows:
- If there is a clause in which both of the variables are set, in a way that falsifies the clause, then the algorithm backtracks to its most recent choice point, undoing the assignments it made since that choice, and reverses the decision made at that choice. If no choice point has been reached, or if the algorithm has already backtracked over the most recent choice point, then it aborts the search and reports that the input 2-CNF formula is unsatisfiable.
- If there is a clause in which one of the variables has been set, and the clause may still become either true or false, then the other variable is set in a way that forces the clause to become true.
- If all clauses are either guaranteed to be true for the current assignment or have two unset variables, then the algorithm creates a choice point and sets one of the unassigned variables to an arbitrarily chosen value.
Intuitively, the algorithm follows all chains of inference after making each of its choices; this either leads to a contradiction and a backtracking step, or, if no contradiction is derived, it follows that the choice was a correct one that leads to a satisfying assignment. Therefore, the algorithm either correctly finds a satisfying assignment or it correctly determines that the input is unsatisfiable.
Even et al. did not describe in detail how to implement this algorithm efficiently; they state only that by "using appropriate data structures in order to find the implications of any decision", each step of the algorithm (other than the backtracking) can be performed quickly. However, some inputs may cause the algorithm to backtrack many times, each time performing many steps before backtracking, so its overall complexity may be nonlinear. To avoid this problem, they modify the algorithm so that, after reaching each choice point, it tests in parallel both alternative assignments for the variable set at the choice point, interleaving both parallel tests to produce a sequential algorithm. As soon as one of these two parallel tests reaches another choice point, the other parallel branch is aborted. In this way, the total time spent performing both parallel tests is proportional to the size of the portion of the input formula whose values are permanently assigned. As a result, the algorithm takes linear time in total.
Strongly connected components
found a simpler linear time procedure for solving 2-satisfiability instances, based on the notion of strongly connected componentStrongly connected component
A directed graph is called strongly connected if there is a path from each vertex in the graph to every other vertex. In particular, this means paths in each direction; a path from a to b and also a path from b to a....
s from graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
.
Two vertices in a directed graph are said to be strongly connected to each other if there is a directed path from one to the other and vice versa. This is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, and the vertices of the graph may be partitioned into strongly connected components, subsets within which every two vertices are strongly connected. There are several efficient linear time algorithms for finding the strongly connected components of a graph, based on depth first search: Tarjan's strongly connected components algorithm
Tarjan's strongly connected components algorithm
Tarjan's Algorithm is a graph theory algorithm for finding the strongly connected components of a graph...
and Gabow's algorithm
Gabow's algorithm
In graph theory, the Cheriyan–Mehlhorn/Gabow algorithm is a linear-time method for finding the strongly connected components of a directed graph. It was discovered in 1996 by Joseph Cheriyan and Kurt Mehlhornand rediscovered in 1999 by Harold N...
each perform a single depth first search. Kosaraju's algorithm
Kosaraju's algorithm
In computer science, the Kosaraju-Sharir algorithm is an algorithm to find the strongly connected components of a directed graph. Aho, Hopcroft and Ullman credit it to an unpublished paper from 1978 by S. Rao Kosaraju and Micha Sharir...
performs two depth first searches, but is very simple: the first search is used only to order the vertices, in the reverse of a postorder depth-first traversal. Then, the second pass of the algorithm loops through the vertices in this order, and for each vertex that has not already been assigned to a component, it performs a depth-first search of the transpose graph
Transpose graph
In the mathematical and algorithmic study of graph theory, the converse, transpose or reverse of a directed graph G is another directed graph on the same set of vertices with all of the edges reversed compared to the orientation of the corresponding edges in G...
starting from that vertex, backtracking when the search reaches a previously-assigned vertices; the unsassigned vertices reached by this search form a new component.
In terms of the implication graph, two terms belong to the same strongly connected component whenever there exist chains of implications from one term to the other and vice versa. Therefore, the two terms must have the same value in any satisfying assignment to the given 2-satisfiability instance. In particular, if a variable and its negation both belong to the same strongly connected component, the instance cannot be satisfied, because it is impossible to assign both of these terms the same value. As Aspvall et al. showed, this is a necessary and sufficient condition: a 2-CNF formula is satisfiable if and only if there is no variable that belongs to the same strongly connected component as its negation.
This immediately leads to a linear time algorithm for testing satisfiability of 2-CNF formulae: simply perform a strong connectivity analysis on the implication graph and check that each variable and its negation belong to different components. However, as Aspvall et al. also showed, it also leads to a linear time algorithm for finding a satisfying assignment, when one exists. Their algorithm performs the following steps:
- Construct the implication graph of the instance, and find its strongly connected components using any of the known linear-time algorithms for strong connectivity analysis.
- Check whether any strongly connected component contains both a variable and its negation. If so, report that the instance is not satisfiable and halt.
- Construct the condensationStrongly connected componentA directed graph is called strongly connected if there is a path from each vertex in the graph to every other vertex. In particular, this means paths in each direction; a path from a to b and also a path from b to a....
of the implication graph, a smaller graph that has one vertex for each strongly connected component, and an edge from component to component whenever the implication graph contains an edge such that belongs to component and belongs to component . The condensation is automatically a directed acyclic graphDirected acyclic graphIn mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
and, like the implication graph from which it was formed, it is skew-symmetric. - Topologically orderTopological sortingIn computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that, for every edge uv, u comes before v in the ordering...
the vertices of the condensation; the order in which the components are generated by Kosaraju's algorithm is automatically a topological ordering. - For each component in this order, if its variables do not already have truth assignments, set all the terms in the component to be false. This also causes all of the terms in the complementary component to be set to true.
Due to the topological ordering, when a term is set to false, all terms that lead to it via a chain of implications will themselves already have been set to false. Symmetrically, when a term is set to true, all terms that can be reached from it via a chain of implications will already have been set to true. Therefore, the truth assignment constructed by this procedure satisfies the given formula, which also completes the proof of correctness of the necessary and sufficient condition identified by Aspvall et al.
As Aspvall et al. show, a similar procedure involving topologically ordering the strongly connected components of the implication graph may also be used to evaluate fully quantified Boolean formulae
True quantified Boolean formula
In computational complexity theory, the language TQBF is a formal language consisting of the true quantified Boolean formulas. A quantified Boolean formula is a formula in quantified propositional logic where every variable is quantified , using either existential or universal quantifiers, at the...
in which the formula being quantified is a 2-CNF formula.
Conflict-free placement of geometric objects
A number of exact and approximate algorithms for the automatic label placementAutomatic label placement
Automatic label placement refers to the computer methods of placing labels automatically on a map or chart. This is related to the typographic design of such labels....
problem are based on 2-satisfiability. This problem concerns placing textual labels on the features of a diagram or map. Typically, the set of possible locations for each label is highly constrained, not only by the map itself (each label must be near the feature it labels, and must not obscure other features), but by each other: two labels will be illegible if they overlap each other. In general, label placement is an NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
problem. However, if each feature has only two possible locations for its label (say, extending to the left and to the right of the feature) then it may be solved in polynomial time. For, in this case, one may create a 2-satisfiability instance that has a variable for each label and constraints preventing each pair of labels from being assigned overlapping positions. If the labels are all congruent rectangles, the corresponding 2-SAT instance can be shown to have only linearly many constraints, leading to near-linear time algorithms for finding a labeling. describe a map labeling problem in which each label is a rectangle that may be placed in one of three positions with respect to a line segment that it labels: it may have the segment as one of its sides, or it may be centered on the segment. They represent these three positions using two binary variables in such a way that, again, testing the existence of a valid labeling becomes a 2-SAT problem.
use this observation as part of an approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
for the problem of finding square labels of the largest possible size for a given set of points, with the constraint that each label has one of its corners on the point that it labels. To find a labeling with a given size, they eliminate squares that, if doubled, would overlap another points, and they eliminate points that can be labeled in a way that cannot possibly overlap with another point's label, and they show that the remaining points have only two possible label placements, allowing the 2-SAT approach to be used. By searching for the largest size that leads to a solvable 2-SAT instance, they find a solution with approximation ratio at most two. Similarly, if each label is rectangular and must be placed in such a way that the point it labels is somewhere along its bottom edge, then using 2-SAT to find the optimal solution in which the label has the point on a bottom corner leads to an approximation ratio of at most two.
Similar reductions to 2-satisfiability have been applied to other geometric placement problems. In graph drawing
Graph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
, if the vertex locations are fixed and each edge must be drawn as a circular arc with one of two possible locations, then the problem of choosing which arc to use for each edge in order to avoid crossings is a 2SAT problem with a variable for each edge and a constraint for each pair of placements that would lead to a crossing. However, in this case it is possible to speed up the solution, compared to an algorithm that builds and then searches an explicit representation of the implication graph, by searching the graph implicitly
Implicit graph
In the study of graph algorithms, an implicit graph representation is a graph whose vertices or edges are not represented as explicit objects in a computer's memory, but rather are determined algorithmically from some more concise input.-Neighborhood representations:The notion of an implicit graph...
.
In VLSI integrated circuit design, if a collection of modules must be connected by wires that can each bend at most once, then again there are two possible routes for the wires, and the problem of choosing which of these two routes to use, in such a way that all wires can be routed in a single layer of the circuit, can be solved as a 2SAT instance.
consider another VLSI design problem: the question of whether or not to mirror-reverse each module in a circuit design. This mirror reversal leaves the module's operations unchanged, but it changes the order of the points at which the input and output signals of the module connect to it, possibly changing how well the module fits into the rest of the design. Boros et al. consider a simplified version of the problem in which the modules have already been placed along a single linear channel, in which the wires between modules must be routed, and there is a fixed bound on the density of the channel (the maximum number of signals that must pass through any cross-section of the channel). They observe that this version of the problem may be solved as a 2-SAT instance, in which the constraints relate the orientations of pairs of modules that are directly across the channel from each other; as a consequence, the optimal density may also be calculated efficiently, by performing a binary search in which each step involves the solution of a 2-SAT instance.
Data clustering
One way of clustering a set of data pointsData clustering
Cluster analysis or clustering is the task of assigning a set of objects into groups so that the objects in the same cluster are more similar to each other than to those in other clusters....
in a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
into two clusters is to choose the clusters in such a way as to minimize the sum of the diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
s of the clusters, where the diameter of any single cluster is the largest distance between any two of its points; this is preferable to minimizing the maximum cluster size, which may lead to very similar points being assigned to different clusters. If the target diameters of the two clusters are known, a clustering that achieves those targets may be found by solving a 2-satisfiability instance. The instance has one variable per point, indicating whether that point belongs to the first cluster or the second cluster. Whenever any two points are too far apart from each other for both to belong to the same cluster, a clause is added to the instance that prevents this assignment.
The same method also can be used as a subroutine when the individual cluster diameters are unknown. To test whether a given sum of diameters can be achieved without knowing the individual cluster diameters, one may try all maximal pairs of target diameters that add up to at most the given sum, representing each pair of diameters as a 2-satisfiability instance and using a 2-satisfiability algorithm to determine whether that pair can be realized by a clustering. To find the optimal sum of diameters one may perform a binary search in which each step is a feasibility test of this type. The same approach also works to find clusterings that optimize other combinations than sums of the cluster diameters, and that use arbitrary dissimilarity numbers (rather than distances in a metric space) to measure the size of a cluster. The time bound for this algorithm is dominated by the time to solve a sequence of 2-SAT instances that are closely related to each other, and shows how to solve these related instances more quickly than if they were solved independently from each other, leading to a total time bound of for the sum-of-diameters clustering problem.
Scheduling
consider a model of classroom scheduling in which a set of n teachers must be scheduled to teach each of m cohorts of students; the number of hours per week that teacher i spends with cohort j is described by entry Rij of a matrix R given as input to the problem, and each teacher also has a set of hours during which he or she is available to be scheduled. As they show, the problem is NP-completeNP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
, even when each teacher has at most three available hours, but it can be solved as an instance of 2-satisfiability when each teacher only has two available hours. (Teachers with only a single available hour may easily be eliminated from the problem.) In this problem, each variable vij corresponds to an hour that teacher i must spend with cohort j, the assignment to the variable specifies whether that hour is the first or the second of the teacher's available hours, and there is a 2-SAT clause preventing any conflict of either of two types: two cohorts assigned to a teacher at the same time as each other, or one cohort assigned to two teachers at the same time.
apply 2-satisfiability to a problem of sports scheduling, in which the pairings of a round-robin tournament
Round-robin tournament
A round-robin tournament is a competition "in which each contestant meets all other contestants in turn".-Terminology:...
have already been chosen and the games must be assigned to the teams' stadiums. In this problem, it is desirable to alternate home and away games to the extent possible, avoiding "breaks" in which a team plays two home games in a row or two away games in a row. At most two teams can avoid breaks entirely, alternating between home and away games; no other team can have the same home-away schedule as these two, because then it would be unable to play the team with which it had the same schedule. Therefore, an optimal schedule has two breakless teams and a single break for every other team. Once one of the breakless teams is chosen, one can set up a 2-satisfiability problem in which each variable represents the home-away assignment for a single team in a single game, and the constraints enforce the properties that any two teams have a consistent assignment for their games, that each team have at most one break before and at most one break after the game with the breakless team, and that no team has two breaks. Therefore, testing whether a schedule admits a solution with the optimal number of breaks can be done by solving a linear number of 2-satisfiability problems, one for each choice of the breakless team. A similar technique also allows finding schedules in which every team has a single break, and maximizing rather than minimizing the number of breaks (to reduce the total mileage traveled by the teams).
Digital tomography
TomographyTomography
Tomography refers to imaging by sections or sectioning, through the use of any kind of penetrating wave. A device used in tomography is called a tomograph, while the image produced is a tomogram. The method is used in radiology, archaeology, biology, geophysics, oceanography, materials science,...
is the process of recovering shapes from their cross-sections.
In digital tomography, a simplified version of the problem that has been frequently studied, the shape to be recovered is a polyomino
Polyomino
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling with a connected interior....
(a subset of the squares in the two-dimensional square lattice
Square lattice
In mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of the integer lattice. It is one of the five types of two-dimensional lattices as classified by their symmetry groups; its symmetry group is known symbolically as p4m.Two...
), and the cross-sections provide aggregate information about the sets of squares in individual rows and columns of the lattice. For instance, in the popular nonogram puzzles, also known as paint by numbers or griddlers, the set of squares to be determined represents the dark pixel
Pixel
In digital imaging, a pixel, or pel, is a single point in a raster image, or the smallest addressable screen element in a display device; it is the smallest unit of picture that can be represented or controlled....
s in a bitmap image
Raster graphics
In computer graphics, a raster graphics image, or bitmap, is a data structure representing a generally rectangular grid of pixels, or points of color, viewable via a monitor, paper, or other display medium...
, and the input given to the puzzle solver tells him or her how many consecutive blocks of dark pixels to include in each row or column of the image, and how long each of those blocks should be. In other forms of digital tomography, even less information about each row or column is given: only the total number of squares, rather than the number and length of the blocks of squares. An equivalent version of the problem is that we must recover a given 0-1 matrix given only the sums of the values in each row and in each column of the matrix.
Although there exist polynomial time algorithms to find a matrix having given row and column sums, the solution may be far from unique: any submatrix in the form of a 2 × 2 identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
can be complemented without affecting the correctness of the solution. Therefore, researchers have searched for constraints on the shape to be reconstructed that can be used to restrict the space of solutions. For instance, one might assume that the shape is connected; however, testing whether there exists a connected solution is NP-complete. An even more constrained version that is easier to solve is that the shape is orthogonally convex: having a single contiguous block of squares in each row and column.
Improving several previous solutions, showed how to reconstruct connected orthogonally convex shapes efficiently, using 2-SAT. The idea of their solution is to guess the indexes of rows containing the leftmost and rightmost cells of the shape to be reconstructed, and then to set up a 2-SAT problem that tests whether there exists a shape consistent with these guesses and with the given row and column sums. They use four 2-SAT variables for each square that might be part of the given shape, one to indicate whether it belongs to each of four possible "corner regions" of the shape, and they use constraints that force these regions to be disjoint, to have the desired shapes, to form an overall shape with contiguous rows and columns, and to have the desired row and column sums. Their algorithm takes time where is the smaller of the two dimensions of the input shape and is the larger of the two dimensions. The same method was later extended to orthogonally convex shapes
that might be connected only diagonally instead of requiring orthogonal connectivity.
More recently, as part of a solver for full nonogram puzzles, used 2-SAT to combine information obtained from several other heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
s. Given a partial solution to the puzzle, they use dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
within each row or column to determine whether the constraints of that row or column force any of its squares to be white or black, and whether any two squares in the same row or column can be connected by an implication relation. They also transform the nonogram into a digital tomography problem by replacing the sequence of block lengths in each row and column by its sum, and use a maximum flow formulation to determine whether this digital tomography problem combining all of the rows and columns has any squares whose state can be determined or pairs of squares that can be connected by an implication relation. If either of these two heuristics determines the value of one of the squares, it is included in the partial solution and the same calculations are repeated. However, if both heuristics fail to set any squares, the implications found by both of them are combined into a 2-satisfiability problem and a 2-satisfiability solver is used to find squares whose value is fixed by the problem, after which the procedure is again repeated. This procedure may or may not succeed in finding a solution, but it is guaranteed to run in polynomial time. Batenburg and Kosters report that, although most newspaper puzzles do not need its full power, both this procedure and a more powerful but slower procedure which combines this 2-SAT approach with the limited backtracking of are significantly more effective than the dynamic programming and flow heuristics without 2-SAT when applied to more difficult randomly generated nonograms.
Other applications
2-satisfiability has also been applied to problems of recognizing undirected graphs that can be partitioned into an independent setIndependent set (graph theory)
In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
and a small number of complete bipartite subgraphs
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
, inferring business relationships among autonomous subsystems of the internet, and reconstruction of evolutionary trees.
NL-completeness
A nondeterministic algorithm for determining whether a 2-satisfiability instance is not satisfiable, using only a logarithmLogarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
ic amount of writable memory, is easy to describe: simply choose (nondeterministically) a variable v and search (nondeterministically) for a chain of implications leading from v to its negation and then back to v. If such a chain is found, the instance cannot be satisfiable. By the Immerman-Szelepcsényi theorem
Immerman-Szelepcsényi theorem
In computational complexity theory, the Immerman–Szelepcsényi theorem was proven independently by Neil Immerman and Róbert Szelepcsényi in 1987, for which they shared the 1995 Gödel Prize. In its general form the theorem states that NSPACE = co-NSPACE for any function s ≥ log n...
, it is also possible in nondeterministic logspace to verify that a satisfiable 2-SAT instance is satisfiable.
2-satisfiability is NL-complete
NL-complete
In computational complexity theory, NL-Complete is a complexity class which is complete for NL. It contains the most "difficult" or "expressive" problems in NL...
, meaning that it is one of the "hardest" or "most expressive" problems in the complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
NL
NL (complexity)
In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space....
of problems solvable nondeterministically in logarithmic space. Completeness here means that a deterministic Turing machine using only logarithmic space can transform any other problem in NL into an equivalent 2-satisfiability problem. Analogously to similar results for the more well-known complexity class NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
, this transformation together with the Immerman-Szelepcsényi theorem allow any problem in NL to be represented as a second order logic formula with a single existentially quantified predicate with clauses limited to length 2; such formulae are known as SO-Krom. Similarly, the implicative normal form can be expressed in first order logic with the addition of an operator for transitive closure
Transitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
.
The set of all solutions
Median graph
In mathematics, and more specifically graph theory, a median graph is an undirected graph in which any three vertices a, b, and c have a unique median: a vertex m that belongs to shortest paths between any two of a, b, and c.The concept of median graphs has long been studied, for instance by or ...
, in which an edge corresponds to the operation of flipping the values of a set of variables that are all constrained to be equal or unequal to each other. In particular, by following edges in this way one can get from any solution to any other solution. Conversely, any median graph can be represented as the set of solutions to a 2-satisfiability instance in this way. The median of any three solutions is formed by setting each variable to the value it holds in the majority
Majority function
In Boolean logic, the majority function is a function from n inputs to one output. The value of the operation is false when n/2 or more arguments are false, and true otherwise....
of the three solutions; this median always forms another solution to the instance.
describes an algorithm for efficiently listing all solutions to a given 2-satisfiability instance, and for solving several related problems.
There also exist algorithms for finding two satisfying assignments that have the maximal Hamming distance
Hamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
from each other.
Counting the number of satisfying assignments
#2SAT is the problem of counting the number of satisfying assignments to a given 2-CNF formula. This counting problemCounting problem
Counting problem may refer to:* Enumeration* Combinatorial enumeration* Counting problem...
is #P-complete, which implies that it is not solvable in polynomial time unless P = NP. Moreover, there is no fully polynomial randomized approximation scheme
Polynomial-time approximation scheme
In computer science, a polynomial-time approximation scheme is a type of approximation algorithm for optimization problems ....
for #2SAT unless NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
= RP
RP (complexity)
In complexity theory, RP is the complexity class of problems for which a probabilistic Turing machine exists with these properties:* It always runs in polynomial time in the input size...
and this even holds when the input is restricted to monotone 2-CNF formulas, i.e., 2-CNF formulas in which each literal
Literal (mathematical logic)
In mathematical logic, a literal is an atomic formula or its negation.The definition mostly appears in proof theory , e.g...
is a positive occurrence of a variable.
The fastest known algorithm for computing the exact number of satisfying assignments to a 2SAT formula runs in time
.Random 2-satisfiability instances
One can form a 2-satisfiability instance at random, for a given number n of variables and m of clauses, by choosing each clause uniformly at random from the set of all possible two-variable clauses. When m is small relative to n, such an instance will likely be satisfiable, but larger values of m have smaller probabilities of being satisfiable. More precisely, if m/n is fixed as a constant α ≠ 1, the probability of satisfiability tends to a limitLimit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
as n goes to infinity: if α < 1, the limit is one, while if α > 1, the limit is zero. Thus, the problem exhibits a phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
at α = 1.
Maximum-2-satisfiability
In the maximum-2-satisfiability problem (MAX-2-SAT), the input is a formula in conjunctive normal formConjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
with two literals
Literal (mathematical logic)
In mathematical logic, a literal is an atomic formula or its negation.The definition mostly appears in proof theory , e.g...
per clause, and the task is to determine the maximum number of clauses that can be simultaneously satisfied by an assignment. MAX-2-SAT is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
and it is a particular case of a maximum satisfiability problem
Maximum satisfiability problem
In computational complexity theory, the Maximum Satisfiability problem is the problem of determining the maximum number of clauses, of a given Boolean formula, that can be satisfied by some assignment...
.
By formulating MAX-2-SAT as a problem of finding a cut
Cut (graph theory)
In graph theory, a cut is a partition of the vertices of a graph into two disjoint subsets. The cut-set of the cut is the set of edges whose end points are in different subsets of the partition. Edges are said to be crossing the cut if they are in its cut-set.In an unweighted undirected graph, the...
(that is, a partition of the vertices into two subsets) maximizing the number of edges that have one endpoint in the first subset and one endpoint in the second, in a graph related to the implication graph, and applying semidefinite programming
Semidefinite programming
Semidefinite programming is a subfield of convex optimization concerned with the optimization of a linear objective functionover the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron....
methods to this cut problem, it is possible to find in polynomial time an approximate solution that satisfies at least 0.940... times the optimal number of clauses. A balanced MAX 2-SAT instance is an instance of MAX 2-SAT where every variable appears positively and negatively with equal weight. For this problem, one can improve the approximation ratio to
.If the unique games conjecture
Unique games conjecture
In computational complexity theory, the Unique Games Conjecture is a conjecture made by Subhash Khot in 2002. The conjecture postulates that the problem of determining the value of a certain type of game, known as a unique game, has NP-hard algorithmic complexity...
is true, then it is impossible to approximate MAX 2-SAT, balanced or not, with an approximation constant better than 0.943... in polynomial time.
Under the weaker assumption that P ≠ NP, the problem is only known to be inapproximable within a constant better than 21/22 = 0.95454...
Various authors have also explored exponential worst-case time bounds for exact solution of MAX-2-SAT instances.
Weighted-2-satisfiability
In the weighted 2-satisfiability problem (W2SAT), the input is an-variable 2SAT instance and an integer , and the problem is to decide whether there exists a satisfying assignment in which at most of the variables are true. One may easily encode the vertex cover problem as a W2SAT problem: given a graph and a bound on the size of a vertex cover, create a variable for each vertex of a graph, and for each edge of the graph create a 2SAT clause . Then the satisfying instances of the resulting 2SAT formula encode solutions to the vertex cover problem, and there is a satisfying assignment with true variables if and only if there is a vertex cover with vertices. Therefore, W2SAT is NP-completeNP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
.
Moreover, in parameterized complexity
Parameterized complexity
Parameterized complexity is a branch of computational complexity theory in computer science that focuses on classifying computational problems according to their inherent difficulty with respect to multiple parameters of the input. The complexity of a problem is then measured as a function in those...
W2SAT provides a natural W[1]-complete problem, which implies that W2SAT is not fixed-parameter tractable unless this holds for all problems in W[1]. That is, it is unlikely that there exists an algorithm for W2SAT whose running time takes the form . Even more strongly, W2SAT cannot be solved in time unless the exponential time hypothesis
Exponential time hypothesis
In computational complexity theory, the exponential time hypothesis is an unproven computational hardness assumption formalized by stating that 3-SAT cannot be solved in subexponential time in the worst case. The exponential time hypothesis, if true, would imply that P ≠ NP...
fails.
Quantified Boolean formulae
As well as finding the first polynomial-time algorithm for 2-satisfiability, also formulated the problem of evaluating fully quantified Boolean formulaeTrue quantified Boolean formula
In computational complexity theory, the language TQBF is a formal language consisting of the true quantified Boolean formulas. A quantified Boolean formula is a formula in quantified propositional logic where every variable is quantified , using either existential or universal quantifiers, at the...
in which the formula being quantified is a 2-CNF formula. The 2-satisfiability problem is the special case of this quantified 2-CNF problem, in which all quantifiers are existential. Krom also developed an effective decision procedure for these formulae; showed that it can be solved in linear time, by an extension of their technique of strongly connected components and topological ordering.