Maximum satisfiability problem
Encyclopedia
In computational complexity theory
, the Maximum Satisfiability problem (MAX-SAT) is the problem of determining the maximum number of clauses, of a given Boolean
formula, that can be satisfied by some assignment. It is an FNP
generalization of SAT
.
The MAX-SAT problem is NP-hard
, since its solution easily leads to the solution of the boolean satisfiability problem
, which is NP-complete
. In particular
for unweighted, and 
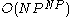for weighted.
From another point of view, it is also APX
-complete, and thus does not admit a PTAS
unless P = NP. MAX-SAT is one of the optimization extensions of the boolean satisfiability problem
, which is the problem of determining if the variables of a given Boolean
formula can be assigned in such a way as to make the formula evaluate to TRUE. If the clauses are restricted to have at most 2 literals, as in 2-satisfiability
, we get the MAX-2SAT problem. If they are restricted to at most 3 literals per clause, as in 3-satisfiability, we get the MAX-3SAT
problem.
Many exact solvers for MAX-SAT have been developed during recent years, and many of them were presented in the well-known conference on the boolean satisfiability problem and related problems, the SAT Conference. In 2006 the SAT Conference hosted the first MAX-SAT evaluation comparing performance of practical solvers for MAX-SAT, as it has done in the past for the pseudo-boolean satisfiability problem and the quantified boolean formula problem.
Because of its NP-hardness, large-size MAX-SAT instances cannot be solved exactly, and one must resort to approximation algorithms
and heuristics
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, the Maximum Satisfiability problem (MAX-SAT) is the problem of determining the maximum number of clauses, of a given Boolean
Propositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
formula, that can be satisfied by some assignment. It is an FNP
FNP (complexity)
In computational complexity theory, the complexity class FNP is the function problem extension of the decision problem class NP. The name is somewhat of a misnomer, since technically it is a class of binary relations, not functions, as the following formal definition explains:This definition does...
generalization of SAT
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
.
The MAX-SAT problem is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
, since its solution easily leads to the solution of the boolean satisfiability problem
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
, which is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
. In particular
for unweighted, and 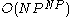for weighted.From another point of view, it is also APX
APX
In complexity theory the class APX is the set of NP optimization problems that allow polynomial-time approximation algorithms with approximation ratio bounded by a constant...
-complete, and thus does not admit a PTAS
Polynomial-time approximation scheme
In computer science, a polynomial-time approximation scheme is a type of approximation algorithm for optimization problems ....
unless P = NP. MAX-SAT is one of the optimization extensions of the boolean satisfiability problem
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
, which is the problem of determining if the variables of a given Boolean
Propositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
formula can be assigned in such a way as to make the formula evaluate to TRUE. If the clauses are restricted to have at most 2 literals, as in 2-satisfiability
2-satisfiability
In computer science, 2-satisfiability is the problem of determining whether a collection of two-valued variables with constraints on pairs of variables can be assigned values satisfying all the constraints...
, we get the MAX-2SAT problem. If they are restricted to at most 3 literals per clause, as in 3-satisfiability, we get the MAX-3SAT
MAX-3SAT
MAX-3SAT is a problem in the computational complexity subfield of computer science. It generalises the Boolean satisfiability problem which is a decision problem considered in complexity theory. It is defined as:Given a 3-CNF formula Φ MAX-3SAT is a problem in the computational complexity...
problem.
Related problems
There are several extensions to MAX-SAT:- The weighted maximum satisfiability problem (Weighted MAX-SAT) asks for the maximum weight which can be satisfied by any assignment, given a set of weighted clauses.
- The partial maximum satisfiability problem (PMAX-SAT) asks for the maximum number of clauses which can be satisfied by any assignment of a given subset of clauses. The rest of the clauses must be satisfied.
- The soft satisfiability problem (soft-SAT), given a set of SAT problems, asks for the maximum number of sets which can be satisfied by any assignment.
- The minimum satisfiability problem.
Many exact solvers for MAX-SAT have been developed during recent years, and many of them were presented in the well-known conference on the boolean satisfiability problem and related problems, the SAT Conference. In 2006 the SAT Conference hosted the first MAX-SAT evaluation comparing performance of practical solvers for MAX-SAT, as it has done in the past for the pseudo-boolean satisfiability problem and the quantified boolean formula problem.
Because of its NP-hardness, large-size MAX-SAT instances cannot be solved exactly, and one must resort to approximation algorithms
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
and heuristics
Metaheuristic
In computer science, metaheuristic designates a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. Metaheuristics make few or no assumptions about the problem being optimized and can search very large spaces...
Solvers
There are several solvers submitted to the last Max-SAT Evaluations:- Branch and BoundBranch and boundBranch and bound is a general algorithm for finding optimal solutions of various optimization problems, especially in discrete and combinatorial optimization...
based: Clone, MaxSatz (based on SatzSatz (SAT solver)SatZ is a well known SAT instance solver. It was developed by Prof. Chu Min Li, a computer science researcher. The Z stands for the last version of SAT solvers.- References :...
), IncMaxSatz, IUT_MaxSatz, WBO. - Satisfiability based: SAT4J, QMaxSat.
- Unsatisfiability based: msuncore, WPM1, PM2.
See also
- Boolean Satisfiability ProblemBoolean satisfiability problemIn computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
- Constraint satisfactionConstraint satisfactionIn artificial intelligence and operations research, constraint satisfaction is the process of finding a solution to a set of constraints that impose conditions that the variables must satisfy. A solution is therefore a vector of variables that satisfies all constraints.The techniques used in...
- Satisfiability Modulo TheoriesSatisfiability Modulo TheoriesIn computer science, the Satisfiability Modulo Theories problem is a decision problem for logical formulas with respect to combinations of background theories expressed in classical first-order logic with equality...
External links
- SAT and MAX-SAT for the lay-researcher
- http://www.satisfiability.org/
- http://www.iiia.csic.es/~maxsat06
- http://www.maxsat.udl.cat
- Weighted Max-2-SAT Benchmarks with Hidden Optimum Solutions
- Lecture Notes on MAX-SAT Approximation