.gif)
Cut (graph theory)
Encyclopedia
In graph theory
, a cut is a partition
of the vertices of a graph into two disjoint subsets. The cut-set of the cut is the set of edges whose end points are in different subsets of the partition. Edges are said to be crossing the cut if they are in its cut-set.
In an unweighted undirected graph, the size or weight of a cut is the number of edges crossing the cut. In a weighted graph, the same term is defined by the sum of the weights of the edges crossing the cut.
In a flow network
, an s-t cut is a cut that requires the source and the sink to be in different subsets, and its cut-set only consists of edges going from the source's side to the sink's side. The capacity of an s-t cut is defined by the sum of capacity
of each edge in the cut-set.
The cut of a graph can sometimes refer to its cut-set instead of the partition.
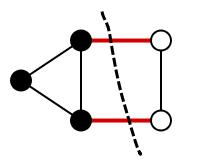A cut is minimum if the size of the cut is not larger than the size of any other cut. The illustration on the right shows a minimum cut: the size of this cut is 2, and there is no cut of size 1 because the graph is bridgeless
.
The max-flow min-cut theorem
proves that the maximum network flow
and the sum of the cut-edge weights of any minimum cut that separates the source and the sink are equal. There are polynomial-time methods to solve the min-cut problem, notably the Edmonds-Karp algorithm
.
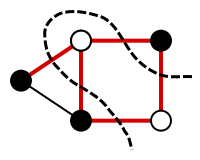A cut is maximum if the size of the cut is not smaller than the size of any other cut. The illustration on the right shows a maximum cut: the size of the cut is equal to 5, and there is no cut of size |E| because the graph is not bipartite
(there is an odd cycle).
In general, finding a maximum cut is computationally hard. The max-cut problem is one of Karp's 21 NP-complete problems
. The max cut problem is also APX-hard, meaning that there is no polynomial-time approximation scheme for it unless P = NP.
Note that min-cut and max-cut are not dual problems in the linear programming
sense, even though one gets from one problem to other by changing min to max in the objective function. The max-flow problem is the dual of the min-cut problem.
approximation due to .
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a cut is a partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the vertices of a graph into two disjoint subsets. The cut-set of the cut is the set of edges whose end points are in different subsets of the partition. Edges are said to be crossing the cut if they are in its cut-set.
In an unweighted undirected graph, the size or weight of a cut is the number of edges crossing the cut. In a weighted graph, the same term is defined by the sum of the weights of the edges crossing the cut.
In a flow network
Flow network
In graph theory, a flow network is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in Operations Research, a directed graph is called a network, the vertices are called nodes and the edges are...
, an s-t cut is a cut that requires the source and the sink to be in different subsets, and its cut-set only consists of edges going from the source's side to the sink's side. The capacity of an s-t cut is defined by the sum of capacity
Capacity of a set
In mathematics, the capacity of a set in Euclidean space is a measure of that set's "size". Unlike, say, Lebesgue measure, which measures a set's volume or physical extent, capacity is a mathematical analogue of a set's ability to hold electrical charge. More precisely, it is the capacitance of...
of each edge in the cut-set.
The cut of a graph can sometimes refer to its cut-set instead of the partition.
Definition
- A cut
is a partition 
of a graph 
.
- An s-t cut
of a network 
is a cut of 
such that 
and 
, where 
and 
are the source and the sink of 
respectively.
- The cut-set of a cut
is the set 
.
- The size of a cut
is the number of edges in the cut-set. If the edges are weighted, the value of the cut is the sum of the weights.
Minimum cut
Bridge (graph theory)
In graph theory, a bridge is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle....
.
The max-flow min-cut theorem
Max-flow min-cut theorem
In optimization theory, the max-flow min-cut theorem states that in a flow network, the maximum amount of flow passing from the source to the sink is equal to the minimum capacity which when removed in a specific way from the network causes the situation that no flow can pass from the source to the...
proves that the maximum network flow
Network flow
In graph theory, a flow network is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in Operations Research, a directed graph is called a network, the vertices are called nodes and the edges are...
and the sum of the cut-edge weights of any minimum cut that separates the source and the sink are equal. There are polynomial-time methods to solve the min-cut problem, notably the Edmonds-Karp algorithm
Edmonds-Karp algorithm
In computer science and graph theory, the Edmonds–Karp algorithm is an implementation of the Ford–Fulkerson method for computing the maximum flow in a flow network in O time. It is asymptotically slower than the relabel-to-front algorithm, which runs in O time, but it is often faster in...
.
Maximum cut
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
(there is an odd cycle).
In general, finding a maximum cut is computationally hard. The max-cut problem is one of Karp's 21 NP-complete problems
Karp's 21 NP-complete problems
One of the most important results in computational complexity theory was Stephen Cook's 1971 demonstration of the first NP-complete problem, the boolean satisfiability problem...
. The max cut problem is also APX-hard, meaning that there is no polynomial-time approximation scheme for it unless P = NP.
Note that min-cut and max-cut are not dual problems in the linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
sense, even though one gets from one problem to other by changing min to max in the objective function. The max-flow problem is the dual of the min-cut problem.
Sparsest cut
The Sparsest cut problem is to bipartition the vertices so as to minimize the ratio of the number of edges across the cut divided by the number of vertices in the smaller half of the partition. This objective function favors solutions that are both sparse (few edges crossing the cut) and balanced (close to a bisection). The problem is known to be NP-Hard, and the best known algorithm is an approximation due to .See also
- Connectivity (graph theory)Connectivity (graph theory)In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
- Prim's algorithmPrim's algorithmIn computer science, Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a connected weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...
- Graph cuts in computer visionGraph cuts in computer visionAs applied in the field of computer vision, graph cuts can be employed to efficiently solve a wide variety of low-level computer vision problems , such as image smoothing, the stereo correspondence problem, and many other computer vision problems that can be formulated in terms of energy minimization...