
Graph cuts in computer vision
Encyclopedia
As applied in the field of computer vision
, graph cuts
can be employed to efficiently solve a wide variety of low-level computer vision problems (early vision), such as image smoothing
, the stereo correspondence problem
, and many other computer vision problems that can be formulated in terms of energy minimization
. Such energy minimization problems can be reduced
to instances of the maximum flow problem
in a graph
(and thus, by the max-flow min-cut theorem
, define a minimal cut of the graph). Under most formulations of such problems in computer vision, the minimum energy solution corresponds to the maximum a posteriori estimate of a solution. Although many computer vision algorithms involve cutting a graph (e.g., normalized cuts), the term "graph cuts" is applied specifically to those models which employ a max-flow/min-cut optimization (other graph cutting algorithms may be considered as graph partitioning algorithms).
"Binary" problems (such as denoising a binary image
) can be solved exactly using this approach; problems where pixels can be labeled with more than two different labels (such as stereo correspondence, or denoising of a grayscale
image) cannot be solved exactly, but solutions produced are usually near the global optimum
.
was first applied in computer vision
in the paper by Greig, Porteous and Seheult of Durham University
. In the Bayesian
statistical context of smoothing
noisy (or corrupted) images, they showed how the maximum a posteriori estimate of a binary image
can be obtained exactly by maximizing the flow
through an associated image network, involving the introduction of a source and sink. The problem was therefore shown to be efficiently solvable. Prior to this result, approximate techniques such as simulated annealing
(as proposed by the Geman brothers), or iterated conditional modes
(a type of greedy algorithm
as suggested by Julian Besag
) ) were used to solve such image smoothing problems.
Although the general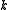 -colour problem
-colour problem
remains unsolved for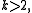 the approach of Greig, Porteous and Seheult has turned out to have wide applicability in general computer vision problems. Greig, Porteous and Seheult approaches are often applied iteratively to a sequence of binary problems, usually yielding near optimal solutions; see the article by Funka-Lea et al. for a recent application.
the approach of Greig, Porteous and Seheult has turned out to have wide applicability in general computer vision problems. Greig, Porteous and Seheult approaches are often applied iteratively to a sequence of binary problems, usually yielding near optimal solutions; see the article by Funka-Lea et al. for a recent application.
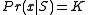
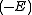
where the Energy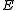 is composed of 2 different models (
is composed of 2 different models (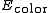 and
and 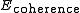 ) :
) :
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, graph cuts
Cut (graph theory)
In graph theory, a cut is a partition of the vertices of a graph into two disjoint subsets. The cut-set of the cut is the set of edges whose end points are in different subsets of the partition. Edges are said to be crossing the cut if they are in its cut-set.In an unweighted undirected graph, the...
can be employed to efficiently solve a wide variety of low-level computer vision problems (early vision), such as image smoothing
Smoothing
In statistics and image processing, to smooth a data set is to create an approximating function that attempts to capture important patterns in the data, while leaving out noise or other fine-scale structures/rapid phenomena. Many different algorithms are used in smoothing...
, the stereo correspondence problem
Correspondence problem
The correspondence problem tries to figure out which parts of an image correspond to which parts of another image, after the camera has moved, time has elapsed, and/or the objects have moved around.-Overview:...
, and many other computer vision problems that can be formulated in terms of energy minimization
Energy minimization
In computational chemistry, energy minimization methods are used to compute the equilibrium configuration of molecules and solids....
. Such energy minimization problems can be reduced
Reduction (complexity)
In computability theory and computational complexity theory, a reduction is a transformation of one problem into another problem. Depending on the transformation used this can be used to define complexity classes on a set of problems....
to instances of the maximum flow problem
Maximum flow problem
In optimization theory, the maximum flow problem is to find a feasible flow through a single-source, single-sink flow network that is maximum....
in a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
(and thus, by the max-flow min-cut theorem
Max-flow min-cut theorem
In optimization theory, the max-flow min-cut theorem states that in a flow network, the maximum amount of flow passing from the source to the sink is equal to the minimum capacity which when removed in a specific way from the network causes the situation that no flow can pass from the source to the...
, define a minimal cut of the graph). Under most formulations of such problems in computer vision, the minimum energy solution corresponds to the maximum a posteriori estimate of a solution. Although many computer vision algorithms involve cutting a graph (e.g., normalized cuts), the term "graph cuts" is applied specifically to those models which employ a max-flow/min-cut optimization (other graph cutting algorithms may be considered as graph partitioning algorithms).
"Binary" problems (such as denoising a binary image
Binary image
A binary image is a digital image that has only two possible values for each pixel. Typically the two colors used for a binary image are black and white though any two colors can be used. The color used for the object in the image is the foreground color while the rest of the image is the...
) can be solved exactly using this approach; problems where pixels can be labeled with more than two different labels (such as stereo correspondence, or denoising of a grayscale
Grayscale
In photography and computing, a grayscale or greyscale digital image is an image in which the value of each pixel is a single sample, that is, it carries only intensity information...
image) cannot be solved exactly, but solutions produced are usually near the global optimum
Global optimum
In mathematics, a global optimum is a selection from a given domain which yields either the highest value or lowest value , when a specific function is applied. For example, for the function...
.
History
The theory of graph cutsCut (graph theory)
In graph theory, a cut is a partition of the vertices of a graph into two disjoint subsets. The cut-set of the cut is the set of edges whose end points are in different subsets of the partition. Edges are said to be crossing the cut if they are in its cut-set.In an unweighted undirected graph, the...
was first applied in computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
in the paper by Greig, Porteous and Seheult of Durham University
Durham University
The University of Durham, commonly known as Durham University, is a university in Durham, England. It was founded by Act of Parliament in 1832 and granted a Royal Charter in 1837...
. In the Bayesian
Bayesian statistics
Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
statistical context of smoothing
Smoothing
In statistics and image processing, to smooth a data set is to create an approximating function that attempts to capture important patterns in the data, while leaving out noise or other fine-scale structures/rapid phenomena. Many different algorithms are used in smoothing...
noisy (or corrupted) images, they showed how the maximum a posteriori estimate of a binary image
Binary image
A binary image is a digital image that has only two possible values for each pixel. Typically the two colors used for a binary image are black and white though any two colors can be used. The color used for the object in the image is the foreground color while the rest of the image is the...
can be obtained exactly by maximizing the flow
Flow network
In graph theory, a flow network is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in Operations Research, a directed graph is called a network, the vertices are called nodes and the edges are...
through an associated image network, involving the introduction of a source and sink. The problem was therefore shown to be efficiently solvable. Prior to this result, approximate techniques such as simulated annealing
Simulated annealing
Simulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...
(as proposed by the Geman brothers), or iterated conditional modes
Iterated conditional modes
In statistics, iterated conditional modes is a deterministic algorithm for obtaining the configuration that maximizes the joint probability of a Markov random field. It does this by iteratively maximizing the probability of each variable conditioned on the rest....
(a type of greedy algorithm
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
as suggested by Julian Besag
Julian Besag
Julian Ernst Besag FRS was a British statistician known chiefly for his work in spatial statistics , and Bayesian inference .- Biography:Besag was born in Loughborough and was educated at Loughborough Grammar School...
) ) were used to solve such image smoothing problems.
Although the general
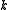 -colour problem
-colour problemGraph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
remains unsolved for
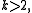 the approach of Greig, Porteous and Seheult has turned out to have wide applicability in general computer vision problems. Greig, Porteous and Seheult approaches are often applied iteratively to a sequence of binary problems, usually yielding near optimal solutions; see the article by Funka-Lea et al. for a recent application.
the approach of Greig, Porteous and Seheult has turned out to have wide applicability in general computer vision problems. Greig, Porteous and Seheult approaches are often applied iteratively to a sequence of binary problems, usually yielding near optimal solutions; see the article by Funka-Lea et al. for a recent application.Notations
- Image : x ∈ {R,G,B}N
- Output : Segmentation (also called opacity) S ∈ RN (soft segmentation). For hard segmentation S ∈ {0=background,1=foreground/object to be detected}
- Energy function : E(x, S, C, λ) where C is the color parameter and λ is the coherence parameter.
-
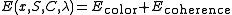
- Optimization : The segmentation can be estimated as a global minimum over S : argminS E(x, S, C, λ)
Existing methods
- Standard Graph cuts: optimize energy function over the segmentation (unknown S value).
- Iterated Graph cuts:
- First step optimizes over the color parameters using K-means.
- Second step performs the usual graph cuts algorithm.
- These 2 steps are repeated recursively until convergence.
- Dynamic graph cuts:
Allows to re-run the algorithm much faster after modifying the problem (e.g. after new seeds have been added by a user).
Energy function
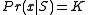
where the Energy
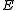 is composed of 2 different models (
is composed of 2 different models (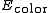 and
and 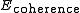 ) :
) : 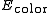 = Likelihood/Color model/Regional term
= Likelihood/Color model/Regional term
- This term can be modeled using different local (e.g. texons) or global (e.g. histograms, GMMs, Adaboost likelihood) approaches that are described below.
Histogram
- We use intensities of pixels marked as seeds to get histograms for object (foreground) and background intensity distributions : P(I|O) and P(I|B).
- Then, we use these histograms to set the regional penalties as negative log-likelihoods.
GMM (Gaussian Mixture Model)
- We usually use 2 distributions to model background and foreground pixels.
- Use a Gaussian mixture model (with 5-8 components) to model those 2 distributions.
- Goal : Try to pull apart those 2 distributions.
Texon
- A texon (or texton) is a set of pixels that has certain characteristics and is repeated in an image.
- Steps :
- Determine a good natural scale for the texture elements.
- Compute non-parametric statistics of the model-interior texons, either on intensity or on Gabor filter responses.
- References :
- Deformable-model based Textured Object Segmentation
- Contour and Texture Analysis for Image Segmentation
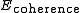 = Prior/Coherence model/Boundary term
= Prior/Coherence model/Boundary term
- Function of the coherence between neighborhood pixels. In practice, pixels are defined as neighbors if they are adjacent either horizontally, vertically or diagonally (4 way connectivity or 8 way connectivity).
- Costs can be based on local intensity gradient, Laplacian zero-crossing, gradient direction, color mixture model,...
Criticism
Graph cuts methods have become popular alternatives to the level set-based approaches for optimizing the location of a contour (see for an extensive comparison). However, graph cut approaches have been criticized in the literature for several issues:- Metrication artifacts: When an image is represented by a 4-connected lattice, graph cuts methods can exhibit unwanted "blockiness" artifacts. Various methods have been proposed for addressing this issue, such as using additional edges or by formulating the max-flow problem in continuous space.
- Shrinking bias: Since graph cuts finds a minimum cut, the algorithm can be biased toward producing a small contour. For example, the algorithm is not well-suited for segmentation of thin objects like blood vessels (see for a proposed fix).
- Multiple labels: Graph cuts is only able to find a global optimum for binary labeling (i.e., two labels) problems, such as foreground/background image segmentation. Extensions have been proposed that can find approximate solutions for multilabel graph cuts problems.
- Memory: the memory usage of graph cuts increase quickly as the image size increase. As an illustration, the Boykov-Kolmogorov max-flow algorithm v2.2 allocates
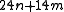 bytes (
bytes ( and
and 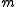 are respectively the number of nodes and edges in the graph). Nevertheless, some amount of work has been recently done in this direction for reducing the graphs before the maximum-flow computation.
are respectively the number of nodes and edges in the graph). Nevertheless, some amount of work has been recently done in this direction for reducing the graphs before the maximum-flow computation.
Algorithm
- Minimization is done using a standard minimum cut algorithm.
- Minimum cut = Maximum flow : we can solve energy minimization by maximizing the flow over the network. The Max Flow problem consists of a directed graph with edges labeled with capacities, and there are two distinct nodes: the source and the sink. Intuitively, it's easy to see that the maximum flow is determined by the bottleneck.
Implementation
Boykov & Kolmogorov published an efficient way to compute the max-flow for computer vision related graph.Software
- http://www.cs.ucl.ac.uk/staff/V.Kolmogorov/software.html
- http://vision.csd.uwo.ca/code/ — some graph cut libraries and MATLAB wrappers

