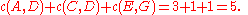Edmonds-Karp algorithm
Encyclopedia
In computer science
and graph theory
, the Edmonds–Karp algorithm is an implementation of the Ford–Fulkerson method for computing the maximum flow
in a flow network
in O(V E2) time. It is asymptotically slower than the relabel-to-front algorithm, which runs in O(V3) time, but it is often faster in practice for sparse graphs. The algorithm was first published by a Soviet scientist, Yefim (Chaim) Dinic, in 1970, and independently by Jack Edmonds
and Richard Karp
in 1972. Dinic's algorithm
includes additional techniques that reduce the running time to O(V2E).
except that the search order when finding the augmenting path is
defined. The path found must be a shortest path that has
available capacity. This can be found by a breadth-first search
, as we let edges have unit length. The running time of
O(V E2) is found by showing that each augmenting path
can be found in O(E) time, that every time at least one of the
E edges becomes saturated, that the distance from the
saturated edge to the source along the augmenting path must be
longer than last time it was saturated, and that the length is
at most V. Another property of this algorithm is
that the length of the shortest augmenting path increases
monotonically. There is an accessible proof in.
algorithm EdmondsKarp
input:
C[1..n, 1..n] (Capacity matrix)
E[1..n, 1..?] (Neighbour lists)
s (Source)
t (Sink)
output:
f (Value of maximum flow)
F (A matrix giving a legal flow with the maximum value)
f := 0 (Initial flow is zero)
F := array(1..n, 1..n) (Residual capacity from u to v is C[u,v] - F[u,v])
forever
m, P := BreadthFirstSearch(C, E, s, t, F)
if m = 0
break
f := f + m
(Backtrack search, and write flow)
v := t
while v ≠ s
u := P[v]
F[u,v] := F[u,v] + m
F[v,u] := F[v,u] - m
v := u
return (f, F)
algorithm BreadthFirstSearch
input:
C, E, s, t, F
output:
M[t] (Capacity of path found)
P (Parent table)
P := array(1..n)
for u in 1..n
P[u] := -1
P[s] := -2 (make sure source is not rediscovered)
M := array(1..n) (Capacity of found path to node)
M[s] := ∞
Q := queue
Q.push(s)
while Q.size > 0
u := Q.pop
for v in E[u]
(If there is available capacity, and v is not seen before in search)
if C[u,v] - F[u,v] > 0 and P[v] = -1
P[v] := u
M[v] := min(M[u], C[u,v] - F[u,v])
if v ≠ t
Q.push(v)
else
return M[t], P
return 0, P
In the pairs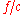
written on the edges, 
is the current flow, and 
is the capacity. The residual capacity from 
to 
is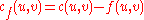 
, the total capacity, minus the flow that is already used. If the net flow from 
to 
is negative, it contributes to the residual capacity.
Notice how the length of the augmenting path found by the algorithm (in red) never decreases. The paths found are the shortest possible. The flow found is equal to the capacity across the minimum cut in the graph separating the source and the sink. There is only one minimal cut in this graph, partitioning the nodes into the sets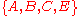
and 
, with the capacity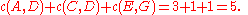
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Edmonds–Karp algorithm is an implementation of the Ford–Fulkerson method for computing the maximum flow
Maximum flow problem
In optimization theory, the maximum flow problem is to find a feasible flow through a single-source, single-sink flow network that is maximum....
in a flow network
Flow network
In graph theory, a flow network is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in Operations Research, a directed graph is called a network, the vertices are called nodes and the edges are...
in O(V E2) time. It is asymptotically slower than the relabel-to-front algorithm, which runs in O(V3) time, but it is often faster in practice for sparse graphs. The algorithm was first published by a Soviet scientist, Yefim (Chaim) Dinic, in 1970, and independently by Jack Edmonds
Jack Edmonds
Jack R. Edmonds is a mathematician, regarded as one of the most important contributors to the field of combinatorial optimization...
and Richard Karp
Richard Karp
Richard Manning Karp is a computer scientist and computational theorist at the University of California, Berkeley, notable for research in the theory of algorithms, for which he received a Turing Award in 1985, The Benjamin Franklin Medal in Computer and Cognitive Science in 2004, and the Kyoto...
in 1972. Dinic's algorithm
Dinic's algorithm
Dinic's algorithm is a strongly polynomial algorithm for computing the maximum flow in a flow network, conceived in 1970 by Israeli computer scientist Yefim Dinitz. The algorithm runs in O time and is similar to the Edmonds–Karp algorithm, which runs in O time, in that it uses shortest augmenting...
includes additional techniques that reduce the running time to O(V2E).
Algorithm
The algorithm is identical to the Ford–Fulkerson algorithm,except that the search order when finding the augmenting path is
defined. The path found must be a shortest path that has
available capacity. This can be found by a breadth-first search
Breadth-first search
In graph theory, breadth-first search is a graph search algorithm that begins at the root node and explores all the neighboring nodes...
, as we let edges have unit length. The running time of
O(V E2) is found by showing that each augmenting path
can be found in O(E) time, that every time at least one of the
E edges becomes saturated, that the distance from the
saturated edge to the source along the augmenting path must be
longer than last time it was saturated, and that the length is
at most V. Another property of this algorithm is
that the length of the shortest augmenting path increases
monotonically. There is an accessible proof in.
Pseudocode
- For a more high level description, see Ford–Fulkerson algorithm.
algorithm EdmondsKarp
input:
C[1..n, 1..n] (Capacity matrix)
E[1..n, 1..?] (Neighbour lists)
s (Source)
t (Sink)
output:
f (Value of maximum flow)
F (A matrix giving a legal flow with the maximum value)
f := 0 (Initial flow is zero)
F := array(1..n, 1..n) (Residual capacity from u to v is C[u,v] - F[u,v])
forever
m, P := BreadthFirstSearch(C, E, s, t, F)
if m = 0
break
f := f + m
(Backtrack search, and write flow)
v := t
while v ≠ s
u := P[v]
F[u,v] := F[u,v] + m
F[v,u] := F[v,u] - m
v := u
return (f, F)
algorithm BreadthFirstSearch
input:
C, E, s, t, F
output:
M[t] (Capacity of path found)
P (Parent table)
P := array(1..n)
for u in 1..n
P[u] := -1
P[s] := -2 (make sure source is not rediscovered)
M := array(1..n) (Capacity of found path to node)
M[s] := ∞
Q := queue
Q.push(s)
while Q.size > 0
u := Q.pop
for v in E[u]
(If there is available capacity, and v is not seen before in search)
if C[u,v] - F[u,v] > 0 and P[v] = -1
P[v] := u
M[v] := min(M[u], C[u,v] - F[u,v])
if v ≠ t
Q.push(v)
else
return M[t], P
return 0, P
Example
Given a network of seven nodes, source A, sink G, and capacities as shown below:In the pairs
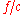written on the edges, is the current flow, and is the capacity. The residual capacity from to is 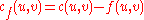, the total capacity, minus the flow that is already used. If the net flow from to is negative, it contributes to the residual capacity.| Capacity | Path |
|---|---|
| Resulting network | |
   |
 |
   |
 |
   |
 |
   |
 |
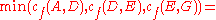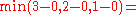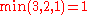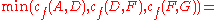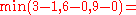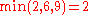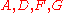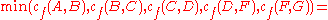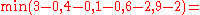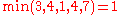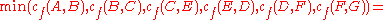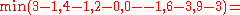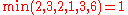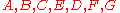Notice how the length of the augmenting path found by the algorithm (in red) never decreases. The paths found are the shortest possible. The flow found is equal to the capacity across the minimum cut in the graph separating the source and the sink. There is only one minimal cut in this graph, partitioning the nodes into the sets
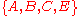and , with the capacity