
Diamond graph
Encyclopedia
In the mathematical
field of graph theory
, the diamond graph is a planar
undirected graph with 4 vertices and 5 edges. It consists of a complete graph
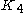 minus one edge.
minus one edge.
The diamond Graph has radius 1, diameter 2, girth 3, chromatic number 3 and chromatic index 3. It is also a 3-vertex-connected
and a 3-edge-connected
graceful
Hamiltonian graph.
s are diamond-free graphs, since every diamond contains a triangle. The Hougardy's conjecture is proved for diamond-free graphs.
The family of graphs in which each connected component
is a cactus graph
is downwardly closed under graph minor operations. This graph family may be characterized by a single forbidden minor. This minor is the diamond graph.
If both the butterfly graph
and the diamond graph are forbidden minors, the family of graphs obtained is the family of pseudoforest
s.
, the direct product
of the cyclic group
Z/2Z with itself.
The characteristic polynomial
of the diamond graph is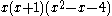 . It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
. It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the diamond graph is a planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
undirected graph with 4 vertices and 5 edges. It consists of a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
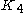 minus one edge.
minus one edge.The diamond Graph has radius 1, diameter 2, girth 3, chromatic number 3 and chromatic index 3. It is also a 3-vertex-connected
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
and a 3-edge-connected
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
graceful
Graceful labeling
In graph theory, a graceful labeling of a graph with e edges is a labeling of its vertices with distinct integers between 0 and e inclusive, such that each edge is uniquely identified by the positive, or absolute difference between its endpoints. A graph which admits a graceful labeling is called a...
Hamiltonian graph.
Diamond-free graphs and forbidden minor
A graph is diamond-free if it has no diamond as an induced subgraph. The triangle-free graphTriangle-free graph
In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
s are diamond-free graphs, since every diamond contains a triangle. The Hougardy's conjecture is proved for diamond-free graphs.
The family of graphs in which each connected component
Connected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
is a cactus graph
Cactus graph
In graph theory, a cactus is a connected graph in which any two simple cycles have at most one vertex in common. Equivalently, every edge in such a graph belongs to at most one simple cycle. Equivalently, every block is an edge or a cycle.-Properties:Cacti are outerplanar graphs...
is downwardly closed under graph minor operations. This graph family may be characterized by a single forbidden minor. This minor is the diamond graph.
If both the butterfly graph
Butterfly graph
In the mathematical field of graph theory, the butterfly graph is a planar undirected graph with 5 vertices and 6 edges...
and the diamond graph are forbidden minors, the family of graphs obtained is the family of pseudoforest
Pseudoforest
In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be...
s.
Algebraic properties
The full automorphism group of the diamond graph is a group of order 4 isomorphic to the Klein four-groupKlein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
, the direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
Z/2Z with itself.
The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the diamond graph is
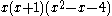 . It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
. It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.

