Nauru graph
Encyclopedia
In the mathematical
field of graph theory
, the Nauru graph is a symmetric
bipartite
cubic graph
with 24 vertices and 36 edges. It was named by David Eppstein
after the twelve-pointed star in the flag of Nauru
.
It has chromatic number 2, chromatic index 3, diameter 4, radius 4 and girth 6. It is also a 3-vertex-connected
and 3-edge-connected
graph.
The smallest cubic graphs with crossing numbers 1–8 are known . The smallest 8-crossing graph is the Nauru graph. There exists 5 non-isomorphic cubic graphs of order 24 with crossing number 8. One of them is the McGee graph
also known as the (3-7)-cage
.
: [5, −9, 7, −7, 9, −5]4.
The Nauru graph can also be constructed as the generalized Petersen graph
G(12, 5) which is formed by the vertices of an dodecagon
, connected to the vertices of a twelve-point star in which each point of the star is connected to the points five steps away from it.
s S4 and S3 and acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Nauru graph is a symmetric graph
(though not distance transitive
). It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the Nauru graph is the only cubic symmetric graph on 24 vertices.
The generalized Petersen graph G(n,k) is vertex-transitive if and only if n = 10 and k =2 or if k2 ≡ ±1 (mod n) and is edge-transitive only in the following seven cases: (n,k) = (4,1), (5,2), (8,3), (10,2), (10,3), (12,5), (24,5). So the Nauru graph is one of only seven symmetric Generalized Petersen graphs. Among these seven graphs are the cubical graph
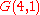, the Petersen graph
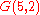, the Möbius–Kantor graph
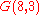, the dodecahedral graph 
and the Desargues graph
.
The Nauru graph is a Cayley graph
of S4, the symmetric group of permutations on four elements, generated by the three different ways of swapping the first element with one of the three others : (1 2), (1 3) and (1 4).
The characteristic polynomial
of the Nauru graph is equal to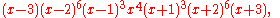
making it an integral graph
—a graph whose spectrum
consists entirely of integers.
as generalized regular polyhedra
: topological surfaces partitioned into edges, vertices, and faces in such a way that there is a symmetry taking any flag (an incident triple of a vertex, edge, and face) into any other flag.
One of these two embeddings forms a torus
, so the Nauru graph is a toroidal graph
: it consists of 12 hexagonal faces together with the 24 vertices and 36 edges of the Nauru graph. The dual graph
of this embedding is a symmetric 6-regular graph with 12 vertices and 36 edges.
The other symmetric embedding of the Nauru graph has six dodecagon
al faces, and forms a surface of genus 4. Its dual is not a simple graph, since each face shares three edges with four other faces, but a multigraph
. This dual can be formed from the graph of a regular octahedron
by replacing each edge with a bundle of three parallel edges.
The set of faces of any one of these two embeddings is the set of Petrie polygon
s of the other embedding.
. It and the prisms are the only generalized Petersen graphs G(n,p) that cannot be so represented in such a way that the symmetries of the drawing form a cyclic group of order n. Instead, its unit distance graph representation has the dihedral group
Dih6 as its symmetry group.
in an effort to collect all the cubic symmetric graphs. The whole list of the cubic symmetric graph is now named after him as the Foster Census and inside this list the Nauru graph is numbered as graph F24A but has no specific name. In 1950, H. S. M. Coxeter cited the graph a second time, giving the Hamiltonian representation used to illustrate this article and describing it as the Levi graph
of a projective configuration discovered by Zacharias.
In 2003, Ed Pegg
wrote in his online MAA column that F24A deserves a name but did not propose one. Finally, in 2007, David Eppstein used the name Nauru graph because the flag
of the Republic of Nauru has a 12-point star similar to the one that appears in the construction of the graph as a generalized Petersen graph.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Nauru graph is a symmetric
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
bipartite
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
with 24 vertices and 36 edges. It was named by David Eppstein
David Eppstein
David Arthur Eppstein is an American computer scientist and mathematician. He is professor of computer science at University of California, Irvine. He is known for his work in computational geometry, graph algorithms, and recreational mathematics.-Biography:Born in England of New Zealander...
after the twelve-pointed star in the flag of Nauru
Flag of Nauru
Following the indepencence of Nauru, the flag of Nauru was raised for the first time.The flag, chosen in a local design competition, was adopted on independence day, January 31, 1968. It depicts Nauru's geographical position, one degree below the Equator. A gold horizontal stripe representing the...
.
It has chromatic number 2, chromatic index 3, diameter 4, radius 4 and girth 6. It is also a 3-vertex-connected
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
and 3-edge-connected
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
graph.
The smallest cubic graphs with crossing numbers 1–8 are known . The smallest 8-crossing graph is the Nauru graph. There exists 5 non-isomorphic cubic graphs of order 24 with crossing number 8. One of them is the McGee graph
McGee graph
In the mathematical field of graph theory, the McGee Graph or the -cage is a 3-regular graph with 24 vertices and 36 edges.The McGeeGraph is the unique -cage . It is also the smallest cubic cage that is not a Moore graph.First discovered by Sachs but unpublished, the graph is named after McGee who...
also known as the (3-7)-cage
Cage (graph theory)
In the mathematical area of graph theory, a cage is a regular graph that has as few vertices as possible for its girth.Formally, an -graph is defined to be a graph in which each vertex has exactly r neighbors, and in which the shortest cycle has length exactly g. It is known that an -graph exists...
.
Construction
The Nauru graph is Hamiltonian and can be described by the LCF notationLCF notation
In combinatorial mathematics, LCF notation or LCF code is a notation devised by Joshua Lederberg, and extended by Coxeter and Frucht, for the representation of cubic graphs that are Hamiltonian. Since the graphs are Hamiltonian, the vertices can be arranged in a cycle, which accounts for two edges...
: [5, −9, 7, −7, 9, −5]4.
The Nauru graph can also be constructed as the generalized Petersen graph
Generalized Petersen graph
In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized...
G(12, 5) which is formed by the vertices of an dodecagon
Dodecagon
In geometry, a dodecagon is any polygon with twelve sides and twelve angles.- Regular dodecagon :It usually refers to a regular dodecagon, having all sides of equal length and all angles equal to 150°...
, connected to the vertices of a twelve-point star in which each point of the star is connected to the points five steps away from it.
Algebraic properties
The automorphism group of the Nauru graph is a group of order 144. It is isomorphic to the direct product of the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
s S4 and S3 and acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Nauru graph is a symmetric graph
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
(though not distance transitive
Distance-transitive graph
In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices v and w at any distance i, and any other two vertices x and y at the same distance, there is an automorphism of the graph that carries v to x and w to y.A distance transitive...
). It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the Nauru graph is the only cubic symmetric graph on 24 vertices.
The generalized Petersen graph G(n,k) is vertex-transitive if and only if n = 10 and k =2 or if k2 ≡ ±1 (mod n) and is edge-transitive only in the following seven cases: (n,k) = (4,1), (5,2), (8,3), (10,2), (10,3), (12,5), (24,5). So the Nauru graph is one of only seven symmetric Generalized Petersen graphs. Among these seven graphs are the cubical graph
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
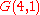, the Petersen graphPetersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
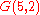, the Möbius–Kantor graphMöbius–Kantor graph
In the mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor...
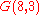, the dodecahedral graph and the Desargues graphDesargues graph
In the mathematical field of graph theory, the Desargues graph is a distance-transitive cubic graph with 20 vertices and 30 edges. It is named after Gérard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial...
.The Nauru graph is a Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of S4, the symmetric group of permutations on four elements, generated by the three different ways of swapping the first element with one of the three others : (1 2), (1 3) and (1 4).
The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Nauru graph is equal to
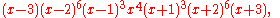
making it an integral graph
Integral graph
In the mathematical field of graph theory, an integral graph is a graph whose spectrum consists entirely of integers. In other words, a graphs is an integral graph if all the eigenvalues of its characteristic polynomial are integers....
—a graph whose spectrum
Spectral graph theory
In mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
consists entirely of integers.
Topological properties
The Nauru graph has two different embeddingsGraph embedding
In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...
as generalized regular polyhedra
Regular map (graph theory)
In mathematics, a regular map is a symmetric tessellation of a closed surface. More precisely, a regular map is a decomposition of a two-dimensional manifold such as a sphere, torus, or Klein bottle into topological disks, such that every flag can be transformed into any other flag by a symmetry...
: topological surfaces partitioned into edges, vertices, and faces in such a way that there is a symmetry taking any flag (an incident triple of a vertex, edge, and face) into any other flag.
One of these two embeddings forms a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, so the Nauru graph is a toroidal graph
Toroidal graph
In mathematics, a graph G is toroidal if it can be embedded on the torus. In other words, the graph's vertices can be placed on a torus such that no edges cross...
: it consists of 12 hexagonal faces together with the 24 vertices and 36 edges of the Nauru graph. The dual graph
Dual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
of this embedding is a symmetric 6-regular graph with 12 vertices and 36 edges.
The other symmetric embedding of the Nauru graph has six dodecagon
Dodecagon
In geometry, a dodecagon is any polygon with twelve sides and twelve angles.- Regular dodecagon :It usually refers to a regular dodecagon, having all sides of equal length and all angles equal to 150°...
al faces, and forms a surface of genus 4. Its dual is not a simple graph, since each face shares three edges with four other faces, but a multigraph
Multigraph
In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....
. This dual can be formed from the graph of a regular octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
by replacing each edge with a bundle of three parallel edges.
The set of faces of any one of these two embeddings is the set of Petrie polygon
Petrie polygon
In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets...
s of the other embedding.
Geometric properties
As with all generalized Petersen graphs, the Nauru graph can be represented by points in the plane in such a way that adjacent vertices are at unit distance apart; that is, it is a unit distance graphUnit distance graph
In mathematics, and particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points by an edge whenever the distance between the two points is exactly one...
. It and the prisms are the only generalized Petersen graphs G(n,p) that cannot be so represented in such a way that the symmetries of the drawing form a cyclic group of order n. Instead, its unit distance graph representation has the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
Dih6 as its symmetry group.
History
The first person to write about the Nauru graph was R. M. FosterR. M. Foster
Ronald Martin Foster , was a Bell Labs mathematician whose work was of significance regarding electronic filters for use on telephone lines...
in an effort to collect all the cubic symmetric graphs. The whole list of the cubic symmetric graph is now named after him as the Foster Census and inside this list the Nauru graph is numbered as graph F24A but has no specific name. In 1950, H. S. M. Coxeter cited the graph a second time, giving the Hamiltonian representation used to illustrate this article and describing it as the Levi graph
Levi graph
In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for...
of a projective configuration discovered by Zacharias.
In 2003, Ed Pegg
Ed Pegg, Jr.
Ed Pegg, Jr. is an expert on mathematical puzzles and is a self-described recreational mathematician. He creates puzzles for the Mathematical Association of America online at Ed Pegg, Jr.'s Math Games. His puzzles have also been used by Will Shortz on the puzzle segment of NPR's Weekend Edition...
wrote in his online MAA column that F24A deserves a name but did not propose one. Finally, in 2007, David Eppstein used the name Nauru graph because the flag
Flag of Nauru
Following the indepencence of Nauru, the flag of Nauru was raised for the first time.The flag, chosen in a local design competition, was adopted on independence day, January 31, 1968. It depicts Nauru's geographical position, one degree below the Equator. A gold horizontal stripe representing the...
of the Republic of Nauru has a 12-point star similar to the one that appears in the construction of the graph as a generalized Petersen graph.