
LCF notation
Encyclopedia
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics, LCF notation or LCF code is a notation devised by Joshua Lederberg
Joshua Lederberg
Joshua Lederberg ForMemRS was an American molecular biologist known for his work in microbial genetics, artificial intelligence, and the United States space program. He was just 33 years old when he won the 1958 Nobel Prize in Physiology or Medicine for discovering that bacteria can mate and...
, and extended by Coxeter
Harold Scott MacDonald Coxeter
Harold Scott MacDonald "Donald" Coxeter, was a British-born Canadian geometer. Coxeter is regarded as one of the great geometers of the 20th century. He was born in London but spent most of his life in Canada....
and Frucht
Robert Frucht
Robert Wertheimer Frucht was a German-Chilean mathematician; his research specialty was graph theory and the symmetries of graphs....
, for the representation of cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
s that are Hamiltonian
Hamiltonian path
In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle in an undirected graph that visits each vertex exactly once and also returns to the starting vertex...
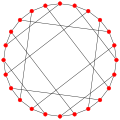
. Since the graphs are Hamiltonian, the vertices can be arranged in a cycle, which accounts for two edges per vertex. The third edge from each vertex can then be described by how many positions clockwise (positive) or counter-clockwise (negative) it leads. Often the pattern repeats, which is indicated by a superscript in the notation. For example, the Nauru graph
Nauru graph
In the mathematical field of graph theory, the Nauru graph is a symmetric bipartite cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru....
, shown on the right, has LCF notation [5, −9, 7, −7, 9, −5]4. Graphs may have different LCF notations, depending on precisely how the vertices are arranged.
The numbers between the square brackets are interpreted modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
N, where N is the number of vertices. Entries equal (modulo N) to 0, 1, and N−1 are not permitted, since they do not correspond to valid third edges.
LCF notation is useful in publishing concise descriptions of Hamiltonian cubic graphs, such as the examples below. In addition, some software packages for manipulating graphs include utilities for creating a graph from its LCF notation.
Examples
| Name | Vertices | LCF notation |
| Tetrahedral Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... graph |
4 | [2]4 |
| Utility graph | 6 | [3]6 |
| Cubical graph | 8 | [3,-3]4 |
| Wagner graph Wagner graph In the mathematical field of graph theory, the Wagner graph is a 3-regular graph with 8 vertices and 12 edges. It is the 8-vertex Möbius ladder graph.-Properties:... |
8 | [4]8 |
| Bidiakis cube Bidiakis cube In the mathematical field of graph theory, the Bidiakis cube is a 3-regular graph with 12 vertices and 18 edges.-Construction:The Bidiakis cube is a cubic Hamiltonian graph and can be defined by the LCF notation [-6,4,-4]4.... |
12 | [6,4,-4]4 or [6,-3,3,6,3,-3]2 |
| Franklin graph Franklin graph In the mathematical field of graph theory, the Franklin graph a 3-regular graph with 12 vertices and 18 edges.The Franklin graph is named after Philip Franklin, who disproved the Heawood conjecture on the number of colors needed when a two-dimensional surface is partitioned into cells by a graph... |
12 | [5,-5]6 or [-5,-3,3,5]3 |
| Frucht graph Frucht graph In the mathematical field of graph theory, the Frucht graph is a 3-regular graph with 12 vertices, 18 edges, and no nontrivial symmetries. It was first described by Robert Frucht in 1939.... |
12 | [-5,-2,-4,2,5,-2,2,5,-2,-5,4,2] |
| Truncated tetrahedral Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... graph |
12 | [2,6,-2]4 |
| Heawood graph Heawood graph In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.-Combinatorial properties:... |
14 | [5,-5]7 |
| Mobius-Kantor graph | 16 | [5,-5]8 |
| Pappus graph Pappus graph In the mathematical field of graph theory, the Pappus graph is a 3-regular undirected graph with 18 vertices and 27 edges, formed as the Levi graph of the Pappus configuration. It is named after Pappus of Alexandria, an ancient Greek mathematician who is believed to have discovered the "hexagon... |
18 | [5,7,-7,7,-7,-5]3 |
| Desargues graph Desargues graph In the mathematical field of graph theory, the Desargues graph is a distance-transitive cubic graph with 20 vertices and 30 edges. It is named after Gérard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial... |
20 | [5,-5,9,-9]5 |
| Dodecahedral graph | 20 | [10,7,4,-4,-7,10,-4,7,-7,4]2 |
| McGee graph McGee graph In the mathematical field of graph theory, the McGee Graph or the -cage is a 3-regular graph with 24 vertices and 36 edges.The McGeeGraph is the unique -cage . It is also the smallest cubic cage that is not a Moore graph.First discovered by Sachs but unpublished, the graph is named after McGee who... |
24 | [12,7,-7]8 |
| Truncated cubical Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... graph |
24 | [2,9,-2,2,-9,-2]4 |
| Truncated octahedral Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... graph |
24 | [3,-7,7,-3]6 |
| Nauru graph Nauru graph In the mathematical field of graph theory, the Nauru graph is a symmetric bipartite cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru.... |
24 | [5,-9,7,-7,9,-5]4 |
| F26A graph F26A graph In the mathematical field of graph theory, the F26A graph is a symmetric bipartite cubic graph with 26 vertices and 39 edges.It has chromatic number 2, chromatic index 3, diameter 5, radius 5 and girth 6... |
26 | [-7, 7]13 |
| Tutte–Coxeter graph | 30 | [-13,-9,7,-7,9,13]5 |
| Dyck graph Dyck graph In the mathematical field of graph theory, the Dyck graph is a 3-regular graph with 32 vertices and 48 edges, named after Walther von Dyck.It is Hamiltonian with 120 distinct Hamiltonian cycles. It has chromatic number 2, chromatic index 3, radius 5, diameter 5 and girth 6... |
32 | [5,-5,13,-13]8 |
| Gray graph Gray graph In the mathematical field of graph theory, the Gray graph is an undirected bipartite graph with 54 vertices and 81 edges. It is a cubic graph: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 , then discovered independently by Bouwer 1968 in reply to a question... |
54 | [-25,7,-7,13,-13,25]9 |
| Truncated dodecahedral graph | 60 | [30, -2, 2, 21, -2, 2, 12, -2, 2, -12, -2, 2, -21, -2, 2, 30, -2, 2, -12, -2, 2, 21, -2, 2, -21, -2, 2, 12, -2, 2]2 |
| Harries graph Harries graph In the mathematical field of graph theory, the Harries graph or Harries -cage is a 3-regular undirected graph with 70 vertices and 105 edges.... |
70 | [-29,-19,-13,13,21,-27,27,33,-13,13,19,-21,-33,29]5 |
| Harries–Wong graph Harries–Wong graph In the mathematical field of graph theory, the Harries–Wong graph is a 3-regular undirected graph with 70 vertices and 105 edges.The Harries–Wong graph has chromatic number 2, chromatic index 3, radius 6, diameter 6, girth 10 and is Hamiltonian... |
70 | [9, 25, 31, -17, 17, 33, 9, -29, -15, -9, 9, 25, -25, 29, 17, -9, 9, -27, 35, -9, 9, -17, 21, 27, -29, -9, -25, 13, 19, -9, -33, -17, 19, -31, 27, 11, -25, 29, -33, 13, -13, 21, -29, -21, 25, 9, -11, -19, 29, 9, -27, -19, -13, -35, -9, 9, 17, 25, -9, 9, 27, -27, -21, 15, -9, 29, -29, 33, -9, -25] |
| Balaban 10-cage Balaban 10-cage In the mathematical field of graph theory, the Balaban 10-cage or Balaban -cage is a 3-regular graph with 70 vertices and 105 edges named after A. T. Balaban. Published in 1972, It was the first -cage discovered but is not unique.... |
70 | [-9, -25, -19, 29, 13, 35, -13, -29, 19, 25, 9, -29, 29, 17, 33, 21, 9,-13, -31, -9, 25, 17, 9, -31, 27, -9, 17, -19, -29, 27, -17, -9, -29, 33, -25,25, -21, 17, -17, 29, 35, -29, 17, -17, 21, -25, 25, -33, 29, 9, 17, -27, 29, 19, -17, 9, -27, 31, -9, -17, -25, 9, 31, 13, -9, -21, -33, -17, -29, 29] |
| Foster graph Foster graph In the mathematical field of graph theory, the Foster graph is a 3-regular graph with 90 vertices and 135 edges.The Foster graph is Hamiltonian and has chromatic number 2, chromatic index 3, radius 8, diameter 8 and girth 10. It is also a 3-vertex-connected and 3-edge-connected graph.All the cubic... |
90 | [17,-9,37,-37,9,-17]15 |
| Biggs-Smith graph | 102 | [16, 24, -38, 17, 34, 48, -19, 41, -35, 47, -20, 34, -36, 21, 14, 48, -16, -36, -43, 28, -17, 21, 29, -43, 46, -24, 28, -38, -14, -50, -45, 21, 8, 27, -21, 20, -37, 39, -34, -44, -8, 38, -21, 25, 15, -34, 18, -28, -41, 36, 8, -29, -21, -48, -28, -20, -47, 14, -8, -15, -27, 38, 24, -48, -18, 25, 38, 31, -25, 24, -46, -14, 28, 11, 21, 35, -39, 43, 36, -38, 14, 50, 43, 36, -11, -36, -24, 45, 8, 19, -25, 38, 20, -24, -14, -21, -8, 44, -31, -38, -28, 37] |
| Balaban 11-cage Balaban 11-cage In the mathematical field of graph theory, the Balaban 11-cage or Balaban -cage is a 3-regular graph with 112 vertices and 168 edges named after A. T. Balaban.The Balaban 11-cage is the unique -cage. It was discovered by Balaban in 1973... |
112 | [44, 26, -47, -15, 35, -39, 11, -27, 38, -37, 43, 14, 28, 51, -29, -16, 41, -11, -26, 15, 22, -51, -35, 36, 52, -14, -33, -26, -46, 52, 26, 16, 43, 33, -15, 17, -53, 23, -42, -35, -28, 30, -22, 45, -44, 16, -38, -16, 50, -55, 20, 28, -17, -43, 47, 34, -26, -41, 11, -36, -23, -16, 41, 17, -51, 26, -33, 47, 17, -11, -20, -30, 21, 29, 36, -43, -52, 10, 39, -28, -17, -52, 51, 26, 37, -17, 10, -10, -45, -34, 17, -26, 27, -21, 46, 53, -10, 29, -50, 35, 15, -47, -29, -41, 26, 33, 55, -17, 42, -26, -36, 16] |
| Ljubljana graph Ljubljana graph In the mathematical field of graph theory, the Ljubljana graph is an undirected bipartite graph with 112 vertices and 168 edges.It is a cubic graph with diameter 8, radius 7, chromatic number 2 and chromatic index 3. Its girth is 10 and there are exactly 168 cycles of length 10 in it... |
112 | [47, -23, -31, 39, 25, -21, -31, -41, 25, 15, 29, -41, -19, 15, -49, 33, 39, -35, -21, 17, -33, 49, 41, 31, -15, -29, 41, 31, -15, -25, 21, 31, -51, -25, 23, 9, -17, 51, 35, -29, 21, -51, -39, 33, -9, -51, 51, -47, -33, 19, 51, -21, 29, 21, -31, -39]2 |
| Tutte 12-cage Tutte 12-cage In the mathematical field of graph theory, the Tutte 12-cage or Benson graph is a 3-regular graph with 126 vertices and 189 edges named after W. T. Tutte.... |
126 | [17, 27, -13, -59, -35, 35, -11, 13, -53, 53, -27, 21, 57, 11, -21, -57, 59, -17]7 |

