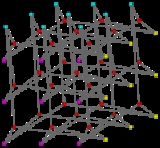
Gray graph
Encyclopedia
In the mathematical
field of graph theory
, the Gray graph is an undirected bipartite graph
with 54 vertices
and 81 edges. It is a cubic graph
: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 (unpublished), then discovered independently by Bouwer 1968 in reply to a question posed by Jon Folkman
1967. The Gray graph is interesting as the first known example of a cubic graph having the algebraic property of being edge but not vertex transitive (see below).
The Gray graph has chromatic number 2, chromatic index 3, radius 6 and diameter 6. It is also a 3-vertex-connected
and 3-edge-connected
non-planar graph
.
of this configuration; it has a vertex for every point and every line of the configuration, and an edge for every pair of a point and a line that touch each other. This construction generalizes (Bouwer 1972) to any dimension n ≥ 3, yielding an n-valent Levi graph with algebraic properties similar to those of the Gray graph.
In (Monson,Pisanski,Schulte,Ivic-Weiss 2007), the Gray graph appears as a different sort of Levi graph for the edges and triangular faces of a certain locally toroidal abstract regular 4-polytope. It is therefore the first in an infinite family of similarly constructed cubic graphs.
Marušič
and Pisanski
(2000) give several alternative methods of constructing the Gray graph. As with any bipartite graph, there are no odd-length cycles
, and there are also no cycles of four or six vertices, so the girth of the Gray graph is 8. The simplest oriented surface on which the Gray graph can be embedded has genus 7 .
The Gray graph is Hamiltonian and can be constructed from the LCF notation
: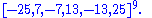
taking every edge to any other edge, but not taking every vertex to any other vertex. The vertices that correspond to points of the underlying configuration can only be symmetric to other vertices that correspond to points, and the vertices that correspond to lines can only be symmetric to other vertices that correspond to lines. Therefore, the Gray graph is a semi-symmetric graph
, the smallest possible cubic semi-symmetric graph.
The characteristic polynomial of the Gray graph is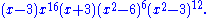
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Gray graph is an undirected bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
with 54 vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
and 81 edges. It is a cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 (unpublished), then discovered independently by Bouwer 1968 in reply to a question posed by Jon Folkman
Jon Folkman
Jon Hal Folkman was an American mathematician, a student of John Milnor, and a researcher at the RAND Corporation.-Schooling:Folkman was a Putnam Fellow in 1960. He received his Ph.D...
1967. The Gray graph is interesting as the first known example of a cubic graph having the algebraic property of being edge but not vertex transitive (see below).
The Gray graph has chromatic number 2, chromatic index 3, radius 6 and diameter 6. It is also a 3-vertex-connected
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
and 3-edge-connected
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
non-planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
.
Construction
The Gray graph can be constructed from the 27 points of a 3×3×3 grid and the 27 axis-parallel lines through these points. This collection of points and lines forms a projective configuration: each point has exactly three lines through it, and each line has exactly three points on it. The Gray graph is the Levi graphLevi graph
In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for...
of this configuration; it has a vertex for every point and every line of the configuration, and an edge for every pair of a point and a line that touch each other. This construction generalizes (Bouwer 1972) to any dimension n ≥ 3, yielding an n-valent Levi graph with algebraic properties similar to those of the Gray graph.
In (Monson,Pisanski,Schulte,Ivic-Weiss 2007), the Gray graph appears as a different sort of Levi graph for the edges and triangular faces of a certain locally toroidal abstract regular 4-polytope. It is therefore the first in an infinite family of similarly constructed cubic graphs.
Marušič
Dragan Marušic
Dragan Marušič is a Slovene mathematician.His research focuses on topics in algebraic graph theory, particularly the symmetry of graphs and the action of finite groups on combinatorial objects. In 2002, he helped show that the Gray graph is the smallest cubic semi-symmetric graph, resolving a...
and Pisanski
Tomaž Pisanski
Tomaž Pisanski is a Slovenian mathematician working mainly in graph theory.In 1980 he calculated the genus of the Cartesian product of any pair of connected, bipartite, d-valent graphs using a method that was later called the White-Pisanski method.In 1982 Vladimir Batagelj and Pisanski proved...
(2000) give several alternative methods of constructing the Gray graph. As with any bipartite graph, there are no odd-length cycles
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
, and there are also no cycles of four or six vertices, so the girth of the Gray graph is 8. The simplest oriented surface on which the Gray graph can be embedded has genus 7 .
The Gray graph is Hamiltonian and can be constructed from the LCF notation
LCF notation
In combinatorial mathematics, LCF notation or LCF code is a notation devised by Joshua Lederberg, and extended by Coxeter and Frucht, for the representation of cubic graphs that are Hamiltonian. Since the graphs are Hamiltonian, the vertices can be arranged in a cycle, which accounts for two edges...
:
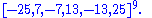
Algebraic properties
The automorphism group of the Gray graph is a group of order 1296. It acts transitively on the edges the graph but not on its vertices : there are symmetriesGraph automorphism
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....
taking every edge to any other edge, but not taking every vertex to any other vertex. The vertices that correspond to points of the underlying configuration can only be symmetric to other vertices that correspond to points, and the vertices that correspond to lines can only be symmetric to other vertices that correspond to lines. Therefore, the Gray graph is a semi-symmetric graph
Semi-symmetric graph
In the mathematical field of graph theory, a semi-symmetric graph is an undirected graph that is edge-transitive and regular, but not vertex-transitive....
, the smallest possible cubic semi-symmetric graph.
The characteristic polynomial of the Gray graph is
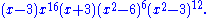
External links
- The Gray Graph Is the Smallest Graph of Its Kind, from MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
.

