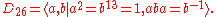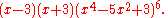F26A graph
Encyclopedia
In the mathematical
field of graph theory
, the F26A graph is a symmetric
bipartite
cubic graph
with 26 vertices and 39 edges.
It has chromatic number 2, chromatic index 3, diameter 5, radius 5 and girth 6. It is also a 3-vertex-connected
and 3-edge-connected
graph.
The F26A graph is Hamiltonian and can be described by the LCF notation
[−7, 7]13.
of the F26A graph is a group of order 78. It acts transitively on the vertices, on the edges, and on the arcs of the graph. Therefore the F26A graph is a symmetric graph
(though not distance transitive
). It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the F26A graph is the only cubic symmetric graph on 26 vertices. It is also a Cayley graph
for the dihedral group
D26, generated by a, ab, and ab4, where:
The F26A graph is the smallest cubic graph where the automorphism group acts regularly on arcs (that is, on edges considered as having a direction).
The characteristic polynomial
of the F26A graph is equal to
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the F26A graph is a symmetric
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
bipartite
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
with 26 vertices and 39 edges.
It has chromatic number 2, chromatic index 3, diameter 5, radius 5 and girth 6. It is also a 3-vertex-connected
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
and 3-edge-connected
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
graph.
The F26A graph is Hamiltonian and can be described by the LCF notation
LCF notation
In combinatorial mathematics, LCF notation or LCF code is a notation devised by Joshua Lederberg, and extended by Coxeter and Frucht, for the representation of cubic graphs that are Hamiltonian. Since the graphs are Hamiltonian, the vertices can be arranged in a cycle, which accounts for two edges...
[−7, 7]13.
Algebraic properties
The automorphism groupGraph automorphism
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....
of the F26A graph is a group of order 78. It acts transitively on the vertices, on the edges, and on the arcs of the graph. Therefore the F26A graph is a symmetric graph
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
(though not distance transitive
Distance-transitive graph
In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices v and w at any distance i, and any other two vertices x and y at the same distance, there is an automorphism of the graph that carries v to x and w to y.A distance transitive...
). It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the F26A graph is the only cubic symmetric graph on 26 vertices. It is also a Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
for the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
D26, generated by a, ab, and ab4, where:
The F26A graph is the smallest cubic graph where the automorphism group acts regularly on arcs (that is, on edges considered as having a direction).
The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the F26A graph is equal to