In the mathematical

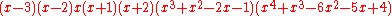Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 field of graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, the Frucht graph is a 3-regular graph

Regular graph

In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...

 with 12 vertices, 18 edges, and no nontrivial symmetries

Graph automorphism

In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....

. It was first described by Robert Frucht

Robert Frucht

Robert Wertheimer Frucht was a German-Chilean mathematician; his research specialty was graph theory and the symmetries of graphs....

 in 1939.

The Frucht graph is a Halin graph

Halin graph

In graph theory, a mathematical discipline, a Halin graph is a planar graph constructed from a plane embedding of a tree with at least four vertices and with no vertices of degree 2, by connecting all the leaves of the tree with a cycle that passes around the tree in the natural cyclic order...

 with chromatic number 3, chromatic index 3, radius 3, diameter 4 and girth 3. As with every Halin graph, the Frucht graph is planar

Planar graph

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...

, 3-vertex-connected

K-vertex-connected graph

In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...

, and polyhedral

Polyhedral graph

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...

. It is also a 3-edge-connected graph

K-edge-connected graph

In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G =  be an arbitrary graph....

.

The Frucht graph is Hamiltonian and can be constructed from the LCF notation

LCF notation

In combinatorial mathematics, LCF notation or LCF code is a notation devised by Joshua Lederberg, and extended by Coxeter and Frucht, for the representation of cubic graphs that are Hamiltonian. Since the graphs are Hamiltonian, the vertices can be arranged in a cycle, which accounts for two edges...

: [−5,−2,−4,2,5,−2,2,5,−2,−5,4,2].

Algebraic properties

The Frucht graph is one of the two smallest cubic graphs possessing only a single graph automorphism

Graph automorphism

In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....

, the identity (that is, every vertex can be distinguished topologically from every other vertex). Such graphs are called asymmetric

Asymmetric graph

In graph theory, a branch of mathematics, an undirected graph is called an asymmetric graph if it has no nontrivial symmetries.Formally, an automorphism of a graph is a permutation p of its vertices with the property that any two vertices u and v are adjacent if and only if p and p are adjacent.The...

 (or identity) graphs. Frucht's theorem

Frucht's theorem

Frucht's theorem is a theorem in algebraic graph theory conjectured by Dénes Kőnig in 1936 and proved by Robert Frucht in 1939. It states that every finite group is the group of symmetries of a finite undirected graph...

 states that any group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

 can be realized as the group of symmetries of a graph, and a strengthening of this theorem also due to Frucht states that any group can be realized as the symmetries of a 3-regular graph; the Frucht graph provides an example of this realization for the trivial group

Trivial group

In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...

.

The characteristic polynomial of the Frucht graph is .
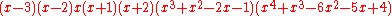