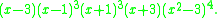Möbius–Kantor graph
Encyclopedia
In the mathematical
field of graph theory
, the Möbius–Kantor graph is a symmetric
bipartite
cubic graph
with 16 vertices and 24 edges named after August Ferdinand Möbius
and Seligmann Kantor. It can be defined as the generalized Petersen graph
G(8,3): that is, it is formed by the vertices of an octagon, connected to the vertices of an eight-point star in which each point of the star is connected to the points three steps away from it.
s with p sides each, having the property that the vertices of one polygon lie on the lines through the edges of the other polygon, and vice versa. If so, the vertices and edges of these polygons would form a projective configuration. For p = 4 there is no solution in the Euclidean plane, but found pairs of polygons of this type, for a generalization of the problem in which the points and edges belong to the complex projective plane. That is, in Kantor's solution, the coordinates of the polygon vertices are complex number
s. Kantor's solution for p = 4, a pair of mutually-inscribed quadrilaterals in the complex projective plane, is called the Möbius–Kantor configuration. supplies the following simple complex projective coordinates for the eight points of the Möbius–Kantor configuration:, (0,0,1), (ω, −1, 1), (−1, 0, 1),, (1,ω,0), (0,1,0), (0,−1,1),
where ω denotes the complex cube root of 1.
More abstractly, the Möbius–Kantor configuration can be described as a system of eight points and eight triples of points such that each point belongs to exactly three of the triples. Any two systems of this type are equivalent under some permutation
of the points; that is, the
Möbius–Kantor configuration is the unique projective configuration of type (8383). The Möbius–Kantor graph derives its name from being the Levi graph
of the Möbius–Kantor configuration. It has one vertex per point and one vertex per triple, with an edge connecting two vertices if they correspond to a point and to a triple that contains that point.
The solution to Möbius' problem of mutually inscribed polygons for values of p greater than four is also of interest. In particular, one possible solution for p = 5 is the Desargues configuration, a set of ten points and ten lines, three points per line and three lines per point, that does admit a Euclidean realization.
The Möbius configuration
is a three-dimensional analogue of the Möbius–Kantor configuration consisting of two mutually inscribed tetrahedra.
, the Möbius–Kantor graph can also be drawn in the plane with all edges unit length, although such a drawing will necessarily have some pairs of crossing edges.
The Möbius–Kantor graph cannot be embedded without crossings in the plane; it has crossing number
4, and is the smallest cubic graph with that crossing number . Additionally, it provides an example of a graph all of whose subgraphs' crossing numbers differ from it by two or more.
However, it is a toroidal graph
: it has an embedding in the torus
in which all faces are hexagons .
There is an even more symmetric embedding of Möbius–Kantor graph in the double torus
which is a regular map
, with six octagonal faces, in which all 96 symmetries of the graph can be realized as symmetries of the embedding; credits this embedding to . Its 96-element symmetry group
has a Cayley graph
that can itself be embedded on the double torus, and was shown by to be the unique group with genus
two. The Cayley graph on 96 vertices is a flag graph of the genus 2 regular map having Möbius–Kantor graph as a sekeleton. This means it can be obtained from the regular map as a skeleton of the dual of its barycentric subdivision. A sculpture by DeWitt Godfrey
and Duane Martinez showing the double torus embedding of the symmetries of the Möbius–Kantor graph was unveiled at the Technical Museum of Slovenia as part of the 6th Slovenian International Conference on Graph Theory in 2007.
The Möbius–Kantor graph admits an embedding into a triple torus
(genus 3 torus) that is a regular map
having four 12-gonal faces; .
, motivated by an investigation of potential chemical structures of carbon compounds, studied the family of all embeddings of the Möbius–Kantor graph onto 2-manifold
s; they showed that there are 759 inequivalent embeddings.
. It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the Möbius–Kantor graph is the unique cubic symmetric graph with 16 vertices, and the smallest cubic symmetric graph which is not also distance-transitive
. The Möbius–Kantor graph is also a Cayley graph
.
The generalized Petersen graph G(n,k) is vertex-transitive if and only if n = 10 and k =2 or if k2 ≡ ±1 (mod n) and is edge-transitive only in the following seven cases: (n,k) = (4,1), (5,2), (8,3), (10,2), (10,3), (12,5), or (24,5) . So the Möbius–Kantor graph is one of only seven symmetric Generalized Petersen graphs. Its symmetric double torus embedding is correspondingly one of only seven regular cubic maps in which the total number of vertices is twice the number of vertices per face . Among the seven symmetric generalized Petersen graphs are the cubical graph
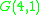, the Petersen graph
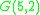, the dodecahedral graph 
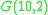, the Desargues graph
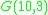and the Nauru graph
.
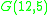The characteristic polynomial
of the Möbius–Kantor graph is equal to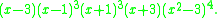
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Möbius–Kantor graph is a symmetric
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
bipartite
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
with 16 vertices and 24 edges named after August Ferdinand Möbius
August Ferdinand Möbius
August Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
and Seligmann Kantor. It can be defined as the generalized Petersen graph
Generalized Petersen graph
In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized...
G(8,3): that is, it is formed by the vertices of an octagon, connected to the vertices of an eight-point star in which each point of the star is connected to the points three steps away from it.
Möbius–Kantor configuration
asked whether there exists a pair of polygonPolygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s with p sides each, having the property that the vertices of one polygon lie on the lines through the edges of the other polygon, and vice versa. If so, the vertices and edges of these polygons would form a projective configuration. For p = 4 there is no solution in the Euclidean plane, but found pairs of polygons of this type, for a generalization of the problem in which the points and edges belong to the complex projective plane. That is, in Kantor's solution, the coordinates of the polygon vertices are complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. Kantor's solution for p = 4, a pair of mutually-inscribed quadrilaterals in the complex projective plane, is called the Möbius–Kantor configuration. supplies the following simple complex projective coordinates for the eight points of the Möbius–Kantor configuration:, (0,0,1), (ω, −1, 1), (−1, 0, 1),, (1,ω,0), (0,1,0), (0,−1,1),
where ω denotes the complex cube root of 1.
More abstractly, the Möbius–Kantor configuration can be described as a system of eight points and eight triples of points such that each point belongs to exactly three of the triples. Any two systems of this type are equivalent under some permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of the points; that is, the
Möbius–Kantor configuration is the unique projective configuration of type (8383). The Möbius–Kantor graph derives its name from being the Levi graph
Levi graph
In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for...
of the Möbius–Kantor configuration. It has one vertex per point and one vertex per triple, with an edge connecting two vertices if they correspond to a point and to a triple that contains that point.
The solution to Möbius' problem of mutually inscribed polygons for values of p greater than four is also of interest. In particular, one possible solution for p = 5 is the Desargues configuration, a set of ten points and ten lines, three points per line and three lines per point, that does admit a Euclidean realization.
The Möbius configuration
Möbius configuration
In geometry, the Möbius configuration is a certain configuration in Euclidean space consisting of two mutually inscribed tetrahedra: each vertex of one tetrahedron lies on a face plane of the other tetrahedron and vice versa...
is a three-dimensional analogue of the Möbius–Kantor configuration consisting of two mutually inscribed tetrahedra.
Relation to hypercube
The Möbius–Kantor graph is a subgraph of the four-dimensional hypercube graph, formed by removing eight edges from the hypercube . Since the hypercube is a unit distance graphUnit distance graph
In mathematics, and particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points by an edge whenever the distance between the two points is exactly one...
, the Möbius–Kantor graph can also be drawn in the plane with all edges unit length, although such a drawing will necessarily have some pairs of crossing edges.
Topology
Crossing number (graph theory)
In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...
4, and is the smallest cubic graph with that crossing number . Additionally, it provides an example of a graph all of whose subgraphs' crossing numbers differ from it by two or more.
However, it is a toroidal graph
Toroidal graph
In mathematics, a graph G is toroidal if it can be embedded on the torus. In other words, the graph's vertices can be placed on a torus such that no edges cross...
: it has an embedding in the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
in which all faces are hexagons .
There is an even more symmetric embedding of Möbius–Kantor graph in the double torus
Double torus
In mathematics, a genus-2 surface is a surface formed by the connected sum of two tori. That is to say, from each of two tori the interior of a disk is removed, and the boundaries of the two disks are identified , forming a double torus.This is the simplest case of the connected sum of n tori...
which is a regular map
Regular map (graph theory)
In mathematics, a regular map is a symmetric tessellation of a closed surface. More precisely, a regular map is a decomposition of a two-dimensional manifold such as a sphere, torus, or Klein bottle into topological disks, such that every flag can be transformed into any other flag by a symmetry...
, with six octagonal faces, in which all 96 symmetries of the graph can be realized as symmetries of the embedding; credits this embedding to . Its 96-element symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
has a Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
that can itself be embedded on the double torus, and was shown by to be the unique group with genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
two. The Cayley graph on 96 vertices is a flag graph of the genus 2 regular map having Möbius–Kantor graph as a sekeleton. This means it can be obtained from the regular map as a skeleton of the dual of its barycentric subdivision. A sculpture by DeWitt Godfrey
DeWitt Godfrey
DeWitt Godfrey is an American sculptor, best known for his large abstract constructions of banded steel installed in public sites. Godfrey was born in Houston, Texas and raised in Kalamazoo, Michigan; he earned a B.A. in Art from Yale University in 1982 and an M.F.A. in Sculpture from the...
and Duane Martinez showing the double torus embedding of the symmetries of the Möbius–Kantor graph was unveiled at the Technical Museum of Slovenia as part of the 6th Slovenian International Conference on Graph Theory in 2007.
The Möbius–Kantor graph admits an embedding into a triple torus
Triple torus
Triple torus or three-torus can refer to one of the two following concepts, both related to a torus.-Three-dimensional torus:The three-dimensional torus, or triple torus, is defined as the Cartesian product of three circles,...
(genus 3 torus) that is a regular map
Regular map (graph theory)
In mathematics, a regular map is a symmetric tessellation of a closed surface. More precisely, a regular map is a decomposition of a two-dimensional manifold such as a sphere, torus, or Klein bottle into topological disks, such that every flag can be transformed into any other flag by a symmetry...
having four 12-gonal faces; .
, motivated by an investigation of potential chemical structures of carbon compounds, studied the family of all embeddings of the Möbius–Kantor graph onto 2-manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s; they showed that there are 759 inequivalent embeddings.
Algebraic properties
The automorphism group of the Möbius–Kantor graph is a group of order 96. It acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Möbius–Kantor graph is a symmetric graphSymmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
. It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the Möbius–Kantor graph is the unique cubic symmetric graph with 16 vertices, and the smallest cubic symmetric graph which is not also distance-transitive
Distance-transitive graph
In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices v and w at any distance i, and any other two vertices x and y at the same distance, there is an automorphism of the graph that carries v to x and w to y.A distance transitive...
. The Möbius–Kantor graph is also a Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
.
The generalized Petersen graph G(n,k) is vertex-transitive if and only if n = 10 and k =2 or if k2 ≡ ±1 (mod n) and is edge-transitive only in the following seven cases: (n,k) = (4,1), (5,2), (8,3), (10,2), (10,3), (12,5), or (24,5) . So the Möbius–Kantor graph is one of only seven symmetric Generalized Petersen graphs. Its symmetric double torus embedding is correspondingly one of only seven regular cubic maps in which the total number of vertices is twice the number of vertices per face . Among the seven symmetric generalized Petersen graphs are the cubical graph
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
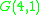, the Petersen graphPetersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
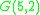, the dodecahedral graph 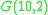, the Desargues graphDesargues graph
In the mathematical field of graph theory, the Desargues graph is a distance-transitive cubic graph with 20 vertices and 30 edges. It is named after Gérard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial...
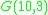and the Nauru graphNauru graph
In the mathematical field of graph theory, the Nauru graph is a symmetric bipartite cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru....
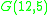.The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Möbius–Kantor graph is equal to