In graph theory

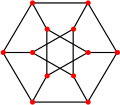
Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, the generalized Petersen graphs are a family of cubic graph

Cubic graph

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....

s formed by connecting the vertices of a regular polygon

Regular polygon

A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

 to the corresponding vertices of a star polygon. They include the Petersen graph

Petersen graph

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...

 and generalize one of the ways of constructing the Petersen graph. The generalized Petersen graph family was introduced in 1950 by H. S. M. Coxeter and these graphs were given their name in 1969 by Mark Watkins.

Definition and notation

In Watkins' notation, G(n,k) is a graph
with vertex set

{u₀, u₁, ..., u_n−1, v₀, v₁, ..., v_n−1}

and edge set

{u_i u_i+1, u_i v_i, v_i v_i+k: i = 0,...,n − 1}

where subscripts are to be read modulo n and k < n/2. Coxeter's notation for the same graph would be {n}+{n/k}, a combination of the Schläfli symbols for the regular n-gon

Regular polygon

A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

 and star polygon from which the graph is formed. Any generalized Petersen graph can also be constructed as a voltage graph

Voltage graph

In graph-theoretic mathematics, a voltage graph is a directed graph whose edges are labelled invertibly by elements of a group. It is formally identical to a gain graph, but it is generally used in topological graph theory as a concise way to specify another graph called the derived graph of the...

 from a graph with two vertices, two self-loops, and one other edge.

The Petersen graph itself is G(5,2) or {5}+{5/2}.

Examples

Among the generalized Petersen graphs are the n-prism G(n,1)
the Dürer graph

Dürer graph

In the mathematical field of graph theory, the Dürer graph is an undirected graph with 12 vertices and 18 edges. It is named after Albrecht Dürer, whose 1514 engraving Melencolia I includes a depiction of Dürer's solid, a convex polyhedron having the Dürer graph as its skeleton...

 G(6,2), the Möbius-Kantor graph
G(8,3), the dodecahedron G(10,2), the Desargues graph

Desargues graph

In the mathematical field of graph theory, the Desargues graph is a distance-transitive cubic graph with 20 vertices and 30 edges. It is named after Gérard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial...

 G(10,3) and the Nauru graph

Nauru graph

In the mathematical field of graph theory, the Nauru graph is a symmetric bipartite cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru....

 G(12,5).

Four generalized Petersen graphs – the 3-prism, the 5-prism, the Dürer graph, and G(7,2) – are among the seven graphs that are cubic

Cubic graph

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....

, 3-vertex-connected

K-vertex-connected graph

In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...

, and well-covered

Well-covered graph

In graph theory, a well-covered graph is an undirected graph in which every minimal vertex cover has the same size as every other minimal vertex cover. Well-covered graphs were defined and first studied by .-Definitions:...

 (meaning that all of their maximal independent set

Maximal independent set

In graph theory, a maximal independent set or maximal stable set is an independent set that is not a subset of any other independent set. That is, it is a set S such that every edge of the graph has at least one endpoint not in S and every vertex not in S has at least one neighbor in S...

s have equal size).

Properties

This family of graphs possesses a number of interesting properties. For example,

1. G(n,k) is vertex-transitive
   Vertex-transitive graph
   In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
   
    (meaning that it has symmetries that take any vertex to any other vertex) if and only if n = 10 and k =2 or if k² ≡ ±1 (mod n).
2. It is edge-transitive
   Edge-transitive graph
   In the mathematical field of graph theory, an edge-transitive graph is a graph G such that, given any two edges e1 and e2 of G, there is anautomorphism of G that maps e1 to e2....
   
    (having symmetries that take any edge to any other edge) only in the following seven cases: (n,k) = (4,1), (5,2), (8,3), (10,2), (10,3), (12,5), (24,5). These seven graphs are therefore the only symmetric
   Symmetric graph
   In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
   
    generalized Petersen graphs.
3. It is bipartite
   Bipartite graph
   In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
   
    if and only if n is even and k is odd.
4. It is a Cayley graph
   Cayley graph
   In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
   
    if and only if k² ≡ 1 (mod n).
5. It is hypohamiltonian
   Hypohamiltonian graph
   In the mathematical field of graph theory, a graph G is said to be hypohamiltonian if G does not itself have a Hamiltonian cycle but every graph formed by removing a single vertex from G is Hamiltonian.-History:...
   
    when n is congruent to 5 modulo 6 and k is 2, n−2, (n+1)/2, or (n−1)/2 (all four of these choice of k lead to isomorphic graphs). It is also non-Hamiltonian when n is divisible by four, at least equal to 8, and k is n/2. In all other cases it has a Hamiltonian cycle. When n is congruent to 3 modulo 6 and k is 2, G(n,k) has exactly three Hamiltonian cycles. For G(n,2), the number of Hamiltonian cycles can be computed by a formula that depends on the congruence class of n modulo six and involves the Fibonacci number
   Fibonacci number
   In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
   
   s.

The Petersen graph itself is the only generalized Petersen graph that is not 3-edge-colorable

Edge coloring

In graph theory, an edge coloring of a graph is an assignment of “colors” to the edges of the graph so that no two adjacent edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several...

.

Every generalized Petersen graph is a unit distance graph

Unit distance graph

In mathematics, and particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points by an edge whenever the distance between the two points is exactly one...

.