Voltage graph
Encyclopedia
In graph-theoretic mathematics
, a voltage graph is a directed graph
whose edges are labelled invertibly by elements of a group
. It is formally identical to a gain graph
, but it is generally used in topological graph theory
as a concise way to specify another graph
called the derived graph of the voltage graph.
Typical choices of the groups used for voltage graphs include the two-element group ℤ2 (for defining the bipartite double cover
of a graph), free group
s (for defining the universal cover
of a graph), d-dimensional integer lattice
s ℤd (viewed as a group under vector addition, for defining periodic structures in d-dimensional Euclidean space
), and finite cyclic group
s ℤn for n > 2. When Π is a cyclic group, the voltage graph may be called a cyclic-voltage graph.
Note that the voltages of a voltage graph need not satisfy Kirchhoff's voltage law, that the sum of voltages around a closed path is 0 (the identity element of the group), although this law does hold for the derived graphs described below. Thus, the name may be somewhat misleading. It results from the origin of voltage graphs as dual to the current graphs of topological graph theory
.
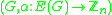is the graph 
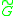whose vertex set is 
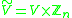and whose edge set is 
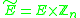, where the endpoints of an edge (e, k) such that e has tail v and head w are 
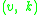and 
.
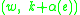Although voltage graphs are defined for digraphs, they may be extended to undirected graphs by replacing each undirected edge by a pair of oppositely ordered directed edges and by requiring that these edges have labels that are inverse to each other in the group structure. In this case, the derived graph will also have the property that its directed edges form pairs of oppositely oriented edges, so the derived graph may itself be interpreted as being an undirected graph.
The derived graph is a covering graph
of the given voltage graph. If no edge label of the voltage graph is the identity element, then the group elements associated with the vertices of the derived graph provide a coloring
of the derived graph with a number of colors equal to the group order. An important special case is the bipartite double cover
, the derived graph of a voltage graph in which all edges are labeled with the non-identity element of a two-element group. Because the order of the group is two, the derived graph in this case is guaranteed to be bipartite
.
Polynomial time algorithm
s are known for determining whether the derived graph of a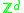
-voltage graph contains any directed cycles.
of a group Π, with a given set Γ of generators, may be defined as the derived graph for a Π-voltage graph having one vertex and |Γ| self-loops, each labeled with one of the generators in Γ.
The Petersen graph
is the derived graph for a ℤ5-voltage graph in the shape of a dumbbell with two vertices and three edges: one edge connecting the two vertices, and one self-loop on each vertex. One self-loop is labeled with 1, the other with 2, and the edge connecting the two vertices is labeled 0. More generally, the same construction allows any generalized Petersen graph
GP(n,k) to be constructed as a derived graph of the same dumbbell graph with labels 1, 0, and k in the group ℤn.
The vertices and edges of any periodic tesellation of the plane may be formed as the derived graph of a finite graph, with voltages in ℤ2.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a voltage graph is a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
whose edges are labelled invertibly by elements of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. It is formally identical to a gain graph
Gain graph
A gain graph is a graph whose edges are labelled "invertibly", or "orientably", by elements of a group G. This means that, if an edge e in one direction has label g , then in the other direction it has label g −1...
, but it is generally used in topological graph theory
Topological graph theory
In mathematics topological graph theory is a branch of graph theory. It studies the embedding of graphs in surfaces, spatial embeddings of graphs, and graphs as topological spaces. It also studies immersions of graphs....
as a concise way to specify another graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
called the derived graph of the voltage graph.
Typical choices of the groups used for voltage graphs include the two-element group ℤ2 (for defining the bipartite double cover
Bipartite double cover
In graph theoretic mathematics, the bipartite double cover of an undirected graph G is a bipartite covering graph of G, with twice as many vertices as G. It can be constructed as the tensor product of graphs G × K2...
of a graph), free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s (for defining the universal cover
Covering graph
In the mathematical discipline of graph theory, a graph C is a covering graph of another graph G if there is a covering map from the vertex set of C to the vertex set of G...
of a graph), d-dimensional integer lattice
Integer lattice
In mathematics, the n-dimensional integer lattice , denoted Zn, is the lattice in the Euclidean space Rn whose lattice points are n-tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. Zn is the simplest example of a root lattice...
s ℤd (viewed as a group under vector addition, for defining periodic structures in d-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
), and finite cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s ℤn for n > 2. When Π is a cyclic group, the voltage graph may be called a cyclic-voltage graph.
Definition
Formal definition of a Π-voltage graph, for a given group Π:- Begin with a digraph G. (The direction is solely for convenience in notation.)
- A Π-voltage on an arc of G is a label of the arc by an element x of Π. For instance, in the case where Π = ℤn, the label is a number i (mod n).
- A Π-voltage assignment is a function
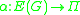that labels each arc of G with a Π-voltage. - A Π-voltage graph is a pair
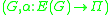such that G is a digraph and α is a voltage assignment. - The voltage group of a voltage graph
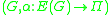is the group Π from which the voltages are assigned.
Note that the voltages of a voltage graph need not satisfy Kirchhoff's voltage law, that the sum of voltages around a closed path is 0 (the identity element of the group), although this law does hold for the derived graphs described below. Thus, the name may be somewhat misleading. It results from the origin of voltage graphs as dual to the current graphs of topological graph theory
Topological graph theory
In mathematics topological graph theory is a branch of graph theory. It studies the embedding of graphs in surfaces, spatial embeddings of graphs, and graphs as topological spaces. It also studies immersions of graphs....
.
The derived graph
The derived graph of a voltage graph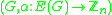 is the graph 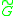whose vertex set is 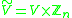and whose edge set is 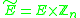, where the endpoints of an edge (e, k) such that e has tail v and head w are 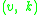and 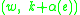.Although voltage graphs are defined for digraphs, they may be extended to undirected graphs by replacing each undirected edge by a pair of oppositely ordered directed edges and by requiring that these edges have labels that are inverse to each other in the group structure. In this case, the derived graph will also have the property that its directed edges form pairs of oppositely oriented edges, so the derived graph may itself be interpreted as being an undirected graph.
The derived graph is a covering graph
Covering graph
In the mathematical discipline of graph theory, a graph C is a covering graph of another graph G if there is a covering map from the vertex set of C to the vertex set of G...
of the given voltage graph. If no edge label of the voltage graph is the identity element, then the group elements associated with the vertices of the derived graph provide a coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
of the derived graph with a number of colors equal to the group order. An important special case is the bipartite double cover
Bipartite double cover
In graph theoretic mathematics, the bipartite double cover of an undirected graph G is a bipartite covering graph of G, with twice as many vertices as G. It can be constructed as the tensor product of graphs G × K2...
, the derived graph of a voltage graph in which all edges are labeled with the non-identity element of a two-element group. Because the order of the group is two, the derived graph in this case is guaranteed to be bipartite
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
.
Polynomial time algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s are known for determining whether the derived graph of a
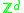-voltage graph contains any directed cycles.Examples
Any Cayley graphCayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of a group Π, with a given set Γ of generators, may be defined as the derived graph for a Π-voltage graph having one vertex and |Γ| self-loops, each labeled with one of the generators in Γ.
The Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
is the derived graph for a ℤ5-voltage graph in the shape of a dumbbell with two vertices and three edges: one edge connecting the two vertices, and one self-loop on each vertex. One self-loop is labeled with 1, the other with 2, and the edge connecting the two vertices is labeled 0. More generally, the same construction allows any generalized Petersen graph
Generalized Petersen graph
In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized...
GP(n,k) to be constructed as a derived graph of the same dumbbell graph with labels 1, 0, and k in the group ℤn.
The vertices and edges of any periodic tesellation of the plane may be formed as the derived graph of a finite graph, with voltages in ℤ2.