
Hypohamiltonian graph
Encyclopedia
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a graph G is said to be hypohamiltonian if G does not itself have a Hamiltonian cycle but every graph formed by removing a single vertex from G is Hamiltonian.
History
Hypohamiltonian graphs were first studied by . cites and as additional early papers on the subject; another early work is by .sums up much of the research in this area with the following sentence: “The articles dealing with those graphs ... usually exhibit new classes of hypohamiltonian or hypotraceable graphs showing that for certain orders n such graphs indeed exist or that they possess strange and unexpected properties.”
Applications
Hypohamiltonian graphs arise in integer programmingInteger programming
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming, which is also known as mixed integer programming.Integer programming is NP-hard...
solutions to the traveling salesman problem: certain kinds of hypohamiltonian graphs define facets
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
of the traveling salesman polytope, a shape defined as the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the set of possible solutions to the traveling salesman problem, and these facets may be used in cutting-plane method
Cutting-plane method
In mathematical optimization, the cutting-plane method is an umbrella term for optimization methods which iteratively refine a feasible set or objective function by means of linear inequalities, termed cuts...
s for solving the problem. observes that the computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
of determining whether a graph is hypohamiltonian, although unknown, is likely to be high, making it difficult to find facets of these types except for those defined by small hypohamiltonian graphs; fortunately, the smallest graphs lead to the strongest inequalities for this application.
Concepts closely related to hypohamiltonicity have also been used by to measure the fault tolerance
Fault-tolerant system
Fault-tolerance or graceful degradation is the property that enables a system to continue operating properly in the event of the failure of some of its components. A newer approach is progressive enhancement...
of network topologies
Network topology
Network topology is the layout pattern of interconnections of the various elements of a computer or biological network....
for parallel computing
Parallel computing
Parallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...
.
Properties
Every hypohamiltonian graph must be 3-vertex-connected, as the removal of any two vertices leaves a Hamiltonian path, which is connected. There exist n-vertex hypohamiltonian graphs in which the maximum degree is n/2, and in which there are approximately n2/4 edges.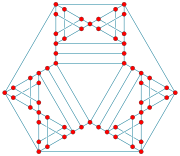
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
, but several examples are now known, the smallest of which has 42 vertices. Every planar hypohamiltonian graph has at least one vertex with only three incident edges.
If a 3-regular graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
is Hamiltonian, its edges can be colored
Edge coloring
In graph theory, an edge coloring of a graph is an assignment of “colors” to the edges of the graph so that no two adjacent edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several...
with three colors: use alternating colors for the edges on the Hamiltonian cycle (which must have even length by the handshaking lemma
Handshaking lemma
In graph theory, a branch of mathematics, the handshaking lemma is the statement that every finite undirected graph has an even number of vertices with odd degree...
) and a third color for all remaining edges. Therefore, all snarks
Snark (graph theory)
In the mathematical field of graph theory, a snark is a connected, bridgeless cubic graph with chromatic index equal to 4. In other words, it is a graph in which every vertex has three neighbors, and the edges cannot be colored by only three colors without two edges of the same color meeting at a...
, bridgeless cubic graphs that require four edge colors, must be non-Hamiltonian, and many known snarks are hypohamiltonian. Every hypohamiltonian snark is bicritical: removing any two vertices leaves a subgraph the edges of which can be colored with only three colors. A three-coloring of this subgraph can be simply described: after removing one vertex, the remaining vertices contain a Hamiltonian cycle. After removing a second vertex, this cycle becomes a path, the edges of which may be colored by alternating between two colors. The remaining edges form a matching and may be colored with a third color.
The color classes of any 3-coloring of the edges of a 3-regular graph form three matchings such that each edge belongs to exactly one of the matchings.
Hypohamiltonian snarks do not have a partition into matchings of this type, but conjectures that the edges of any hypohamiltonian snark may be used to form six matchings such that each edge belongs to exactly two of the matchings. This is a special case of the Berge–Fulkerson conjecture that any snark has six matchings with this property.
Hypohamiltonian graphs cannot be bipartite: in a bipartite graph, a vertex can only be deleted to form a Hamiltonian subgraph if it belongs to the larger of the graph's two color classes. However, every bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
occurs as an induced subgraph of some hypohamiltonian graph.
Examples
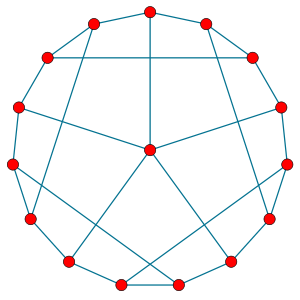
The smallest hypohamiltonian graph is the Petersen graphPetersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
. More generally, the generalized Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
GP(n,2) is hypohamiltonian when n is 5 (mod 6); the Petersen graph is the instance of this construction with n = 5.
found another infinite class of cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
s in which the number of vertices is 4 (mod 6). Lindgren's construction consists of a cycle of length 3 (mod 6) and a single central vertex; the central vertex is connected to every third vertex of the cycle by edges he calls spokes, and the vertices two positions away from each spoke endpoint are connected to each other. Again, the smallest instance of Lindgren's construction is the Petersen graph.
Additional infinite families are given by , , and .
Enumeration
Václav ChvátalVáclav Chvátal
Václav Chvátal is a professor in the Department of Computer Science and Software Engineering at Concordia University in Montreal, Canada, where he holds theCanada Research Chair in Combinatorial Optimization....
proved in 1973 that for all sufficiently large n there exists a hypohamiltonian graph with n vertices. Taking into account subsequent discoveries, “sufficiently large” is now known to mean that such graphs exist for all n ≥ 18. A complete list of hypohamiltonian graphs with at most 17 vertices is known: they are the 10-vertex Petersen graph, a 13-vertex graph and a 15-vertex graph found by computer searches of , and four 16-vertex graphs. There exist at least thirteen 18-vertex hypohamiltonian graphs. By applying the flip-flop method of to the Petersen graph and the flower snark
Flower snark
In the mathematical field of graph theory, the flower snarks form an infinite family of snarks introduced by Rufus Isaacs in 1975.As snarks, the flower snarks are a connected, bridgeless cubic graphs with chromatic index equal to 4...
, it is possible to show that the number of hypohamiltonian graphs, and more specifically the number of hypohamiltonian snarks, grows as an exponential function of the number of vertices.
Generalizations
Graph theorists have also studied hypotraceable graphs, graphs that do not contain a Hamiltonian path but such that every subset of n − 1 vertices may be connected by a path. Analogous definitions of hypohamiltonicity and hypotraceability for directed graphDirected graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
s have been considered by several authors.
An equivalent definition of hypohamiltonian graphs is that their longest cycle has length n − 1 and that the intersection of all longest cycles is empty. investigate graphs with the same property that the intersection of longest cycles is empty but in which the longest cycle length is shorter than n − 1. defines the cyclability of a graph as the largest number k such that every k vertices belong to a cycle; the hypohamiltonian graphs are exactly the graphs that have cyclability n − 1. Similarly, define a graph to be ƒ-fault hamiltonian if the removal of at most ƒ vertices leaves a Hamiltonian subgraph. study the graphs with cyclability n − 2.

