
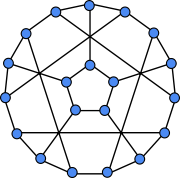
Snark (graph theory)
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a snark is a connected
Connectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
, bridgeless
Bridge (graph theory)
In graph theory, a bridge is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle....
cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
with chromatic index equal to 4. In other words, it is a graph in which every vertex has three neighbors, and the edges cannot be colored by only three colors without two edges of the same color meeting at a point. In order to avoid trivial cases, snarks are often restricted to have girth at least 5.
Writing in The Electronic Journal of Combinatorics, Miroslav Chladný states that
History
P. G. TaitPeter Guthrie Tait
Peter Guthrie Tait FRSE was a Scottish mathematical physicist, best known for the seminal energy physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory, which contributed to the eventual formation of topology as a mathematical...
initiated the study of snarks in 1880, when he proved that the four color theorem
Four color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
is equivalent to the statement that no snark is planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
. The first known snark was the Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
, discovered in 1898. In 1946, Croatian
Croats
Croats are a South Slavic ethnic group mostly living in Croatia, Bosnia and Herzegovina and nearby countries. There are around 4 million Croats living inside Croatia and up to 4.5 million throughout the rest of the world. Responding to political, social and economic pressure, many Croats have...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Danilo Blanuša
Danilo Blanuša
Danilo Blanuša was a Croatian mathematician, physicist, engineer and a professor at the University of Zagreb. He was Serb and he was born in Austro-Ugarska monarchy ....
discovered two more snarks, both on 18 vertices, now named the Blanuša snarks
Blanuša snarks
In the mathematical field of graph theory, the Blanuša snarks are two 3-regular graphs with 18 vertices and 27 edges. They were discovered by Croatian mathematician Danilo Blanuša in 1946 and are named after him. When discovered, only one snark was known—the Petersen graph.As snarks, the Blanuša...
. The fourth known snark was found two years later by Bill Tutte, under the pseudonym Blanche Descartes
Blanche Descartes
Blanche Descartes was a collaborative pseudonym used by the English mathematicians R. Leonard Brooks, Arthur Harold Stone, Cedric Smith, and W. T. Tutte. The four mathematicians met in 1935 as undergraduate students at Trinity College, Cambridge, where they joined the Trinity Mathematical Society...
, and was a graph of order 210. In 1973, George Szekeres
George Szekeres
George Szekeres AM was a Hungarian-Australian mathematician.-Early years:Szekeres was born in Budapest, Hungary as Szekeres György and received his degree in chemistry at the Technical University of Budapest. He worked six years in Budapest as an analytical chemist. He married Esther Klein in 1936...
found the fifth known snark — the Szekeres snark
Szekeres snark
In the mathematical field of graph theory, the Szekeres snark is a snark with 50 vertices and 75 edges. It was the fifth known snark, discovered by George Szekeres in 1973....
. In 1975, Rufus Isaacs
Rufus Isaacs (game theorist)
Rufus Philip Isaacs was a game theorist especially prominent in the 1950s and 1960s with his work on differential games.-Biography:...
generalized Blanuša's method to construct two infinite families of snarks : the flower snark
Flower snark
In the mathematical field of graph theory, the flower snarks form an infinite family of snarks introduced by Rufus Isaacs in 1975.As snarks, the flower snarks are a connected, bridgeless cubic graphs with chromatic index equal to 4...
and the BDS or Blanuša–Descartes–Szekeres snark, a family that includes the two Blanuša snarks, the Descartes snark and the Szekeres snark. Isaacs also discovered a 30-vertices snark that does not belong to the BDS family and that is not a flower snark: the double-star snark
Double-star snark
In the mathematical field of graph theory, the double-star snark is a snark with 30 vertices and 45 edges.In 1975, Rufus Isaacs introduced two infinite families of snarks—the flower snark and the BDS snark, a family that includes the two Blanuša snarks, the Descartes snark and the Szekeres snark...
.
Snarks were so named by the American mathematician Martin Gardner
Martin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
in 1976, after the mysterious and elusive object of the poem The Hunting of the Snark
The Hunting of the Snark
The Hunting of the Snark is usually thought of as a nonsense poem written by Lewis Carroll in 1874, when he was 42 years old...
by Lewis Carroll
Lewis Carroll
Charles Lutwidge Dodgson , better known by the pseudonym Lewis Carroll , was an English author, mathematician, logician, Anglican deacon and photographer. His most famous writings are Alice's Adventures in Wonderland and its sequel Through the Looking-Glass, as well as the poems "The Hunting of the...
.
Properties
All snarks are non-Hamiltonian, and many known snarks are hypohamiltonianHypohamiltonian graph
In the mathematical field of graph theory, a graph G is said to be hypohamiltonian if G does not itself have a Hamiltonian cycle but every graph formed by removing a single vertex from G is Hamiltonian.-History:...
: the removal of any single vertex leaves a Hamiltonian subgraph. A hypohamiltonian snark must be bicritical: the removal of any two vertices leaves a 3-edge-colorable subgraph.
It is conjectured (the cycle double cover conjecture) that in every bridgeless graph one can find a collection of cycles covering each edge twice, or equivalently that the graph can be embedded
Graph embedding
In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...
onto a surface in such a way that all faces of the embedding are simple cycles. Snarks form the difficult case for this conjecture: if it is true for snarks, it is true for all graphs. In this connection, Branko Grünbaum
Branko Grünbaum
Branko Grünbaum is a Croatian-born mathematician and a professor emeritus at the University of Washington in Seattle. He received his Ph.D. in 1957 from Hebrew University of Jerusalem in Israel....
conjectured that it was not possible to embed any snark onto a surface in such a way that all faces are simple cycles and such that every two faces either are disjoint or share only a single edge; however, a counterexample to Grünbaum's conjecture was found by Martin Kochol.
Snark theorem
W. T. TutteW. T. Tutte
William Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...
conjectured that every snark has the Petersen graph as a minor
Minor (graph theory)
In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....
. That is, he conjectured that the smallest snark, the Petersen graph, may be formed from any other snark by contracting some edges and deleting others. Equivalently (because the Petersen graph has maximum degree three) every snark has a subgraph that can be formed from the Petersen graph by subdividing some of its edges
Homeomorphism (graph theory)
In graph theory, two graphs G and G' are homeomorphic if there is an isomorphism from some subdivision of G to some subdivision of G'...
. This conjecture is a strengthened form of the four color theorem, because any graph containing the Petersen graph as a minor must be nonplanar. In 2001, Robertson
Neil Robertson (mathematician)
G. Neil Robertson is a mathematician working mainly in topological graph theory, currently a distinguished professor at the Ohio State University. He earned his Ph.D. in 1969 at the University of Waterloo under his doctoral advisor William Tutte. According to the criteria of the Erdős Number...
, Sanders
Daniel P. Sanders
Daniel P. Sanders is known for his work a new efficient proof of proving the Four color theorem . He was formerly a guest professor of the department of computer science at Columbia University.Sanders received his Ph.D...
, Seymour, and Thomas
Robin Thomas (mathematician)
Robin Thomas is a mathematician working in graph theory at the Georgia Institute of Technology.Thomas received his doctorate in 1985 from Charles University in Prague, Czechoslovakia , under the supervision of Jaroslav Nešetřil...
announced a proof of this conjecture, and the result is now known as the snark theorem. See the Hadwiger conjecture
Hadwiger conjecture (graph theory)
In graph theory, the Hadwiger conjecture states that, if all proper colorings of an undirected graph G use k or more colors, then one can find k disjoint connected subgraphs of G such that each subgraph is connected by an edge to each other subgraph...
for other problems and results relating graph coloring to graph minors.
Tutte also conjectured a generalization of the snark theorem to arbitrary graphs: every bridgeless graph with no Petersen minor has a nowhere zero 4-flow
Nowhere-zero flows
In graph theory, nowhere-zero flows are a special type of network flow which is related to coloring planar graphs. Let G = be a directed graph and let M be an abelian group...
. That is, the edges of the graph may be assigned a direction, and a number from the set {1, 2, 3}, such that the sum of the incoming numbers minus the sum of the outgoing numbers at each vertex is divisible by four. As Tutte showed, for cubic graphs such an assignment exists if and only if the edges can be colored by three colors, so the conjecture follows from the snark theorem in this case. However, this conjecture remains open for graphs that need not be cubic.
List of snarks
- Petersen graphPetersen graphIn the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
(10 vertices; discovered in 1898) - Tietze's graphTietze's graphIn the mathematical field of graph theory, the Tietze's graph is an undirected cubic graph with 12 vertices and 18 edges, formed by applying a Y-Δ transform to the Petersen graph and thereby replacing one of its vertices by a triangle....
(12 vertices but with a girth of 3, generally not considered as a snark) - Blanuša snarksBlanuša snarksIn the mathematical field of graph theory, the Blanuša snarks are two 3-regular graphs with 18 vertices and 27 edges. They were discovered by Croatian mathematician Danilo Blanuša in 1946 and are named after him. When discovered, only one snark was known—the Petersen graph.As snarks, the Blanuša...
(two with 18 vertices; discovered in 1946) - Descartes snarkDescartes snarkIn the mathematical field of graph theory, a Descartes snark is an undirected graph with 210 vertices and 315 edges. It is a snark, first discovered by William Tutte in 1948 under the pseudonym Blanche Descartes....
(210 vertices; discovered by Bill Tutte in 1948) - Double-star snarkDouble-star snarkIn the mathematical field of graph theory, the double-star snark is a snark with 30 vertices and 45 edges.In 1975, Rufus Isaacs introduced two infinite families of snarks—the flower snark and the BDS snark, a family that includes the two Blanuša snarks, the Descartes snark and the Szekeres snark...
(30 vertices) - Szekeres snarkSzekeres snarkIn the mathematical field of graph theory, the Szekeres snark is a snark with 50 vertices and 75 edges. It was the fifth known snark, discovered by George Szekeres in 1973....
(50 vertices; discovered in 1973) - Watkins snarkWatkins snarkIn the mathematical field of graph theory, the Watkins snark is a snark with 50 vertices and 75 edges. It was discovered by John J. Watkins in 1989.As a snark, the Watkins graph is a connected, bridgeless cubic graph with chromatic index equal to 4...
(50 vertices; discovered in 1989) - Flower snarkFlower snarkIn the mathematical field of graph theory, the flower snarks form an infinite family of snarks introduced by Rufus Isaacs in 1975.As snarks, the flower snarks are a connected, bridgeless cubic graphs with chromatic index equal to 4...
(infinite family on 20, 28, 36, 44... vertices; discovered in 1975)
External links
- Alen Orbanić, Tomaž Pisanski, Milan Randić, and Brigite Servatius (preprint). "Blanuša Double". Institute for Mathematics, Physics and Mechanics in Ljubljana, Slovenia.

