Random graph
Encyclopedia
In mathematics
, a random graph is a graph
that is generated by some random process. The theory of random graphs lies at the intersection between graph theory
and probability theory
, and studies the properties of typical random graphs.
s on graphs. Most commonly studied is the one proposed by Edgar Gilbert
, denoted G(n,p), in which every possible edge occurs independently with probability p. A closely related model, the Erdős–Rényi model
denoted G(n,M), assigns equal probability to all graphs with exactly M edges. The latter model can be viewed as a snapshot at a particular time (M) of the random graph process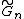
, which is a stochastic process
that starts with n vertices and no edges, and at each step adds one new edge chosen uniformly from the set of missing edges.
If instead we start with an infinite set of vertices, and again let every possible edge occur independently with probability p, then we get an object G called an infinite random graph. Except in the trivial cases when p is 0 or 1, such a G almost surely
has the following property:
It turns out that if the vertex set is countable then there is, up to
isomorphism
, only a single graph with this property, namely the Rado graph
. Thus any countably infinite random graph is almost surely the Rado graph, which for this reason is sometimes called simply the random graph. However, the analogous result is not true for uncountable graphs, of which there are many (nonisomorphic) graphs satisfying the above property.
Another model, which generalizes Gilbert's random graph model, is the random dot-product model. A random dot-product graph associates with each vertex a real vector. The probability of an edge uv between any vertices u and v is some function of the dot product
u • v of their respective vectors.
The network probability matrix
models random graphs through edge probabilities, which represent the probability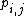
that a given edge 
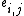exists for a specified time period. This model is extensible to directed and undirected; weighted and unweighted; and static or dynamic graphs.
For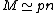
the two most widely used models, G(n,M) and G(n,p), are almost interchangeable.
Random regular graphs form a special case, with properties that may differ from random graphs in general.
. In studying such questions, researchers often concentrate on the asymptotic behavior of random graphs—the values that various probabilities converge to as n grows very large. Percolation theory
characterizes the connectedness of random graphs, especially infinitely large ones.
Percolation is related to the robustness of the graph (called also network). Given a random graph of n nodes and an average degree. Next we remove randomly a fraction 1-p of nodes and leave only a fraction p. There exists a critical percolation threshold pc=1/ below which the network becomes fragmented while above pc a giant connected component exists
.
(threshold functions, evolution of G~)
Random graphs are widely used in the probabilistic method
, where one
tries to prove the existence of graphs with certain properties. The existence of
a property on a random graph can often imply, via the famous Szemerédi regularity lemma
, the existence of that property on almost all graphs.
is a tree
or arborescence
that is formed by a stochastic process
. Types of random trees include uniform spanning tree, random minimal spanning tree
, random binary tree
, treap
, rapidly-exploring random tree
, Brownian tree
, and random forest
.
networks depend on nodes in other networks. This dependency is enhanced by the
developments in modern technology. Such dependencies may lead to cascading failures
between the networks and a relatively small damage can lead to a catastrophic
breakdown of the system. Blackouts are a fascinating demonstration of the important
role played by the dependencies between networks. A recent study developed a
framework to study the cascading failures in an interdependent networks system
in their 1959 paper "On Random Graphs" and independently by Gilbert in his paper "Random graphs".
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a random graph is a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
that is generated by some random process. The theory of random graphs lies at the intersection between graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
and probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, and studies the properties of typical random graphs.
Random graph models
A random graph is obtained by starting with a set of n vertices and adding edges between them at random. Different random graph models produce different probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s on graphs. Most commonly studied is the one proposed by Edgar Gilbert
Edgar Gilbert
Edgar Nelson Gilbert was an American mathematician and coding theorist, a longtime researcher at Bell Laboratories whose accomplishments include the Gilbert–Varshamov bound in coding theory, the Gilbert–Elliott model of bursty errors in signal transmission, and the Erdős–Rényi model for random...
, denoted G(n,p), in which every possible edge occurs independently with probability p. A closely related model, the Erdős–Rényi model
Erdos–Rényi model
In graph theory, the Erdős–Rényi model, named for Paul Erdős and Alfréd Rényi, is either of two models for generating random graphs, including one that sets an edge between each pair of nodes with equal probability, independently of the other edges...
denoted G(n,M), assigns equal probability to all graphs with exactly M edges. The latter model can be viewed as a snapshot at a particular time (M) of the random graph process
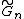, which is a stochastic processStochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
that starts with n vertices and no edges, and at each step adds one new edge chosen uniformly from the set of missing edges.
If instead we start with an infinite set of vertices, and again let every possible edge occur independently with probability p, then we get an object G called an infinite random graph. Except in the trivial cases when p is 0 or 1, such a G almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
has the following property:
- Given any
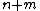elements 
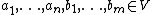, there is a vertex 
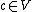that is adjacent to each of 
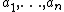and is not adjacent to any of 
.
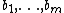It turns out that if the vertex set is countable then there is, up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
, only a single graph with this property, namely the Rado graph
Rado graph
In the mathematical field of graph theory, the Rado graph, also known as the random graph or the Erdős–Renyi graph, is the unique countable graph R such that for any finite graph G and any vertex v of G, any embedding of G − v as an induced subgraph of R can be extended to an...
. Thus any countably infinite random graph is almost surely the Rado graph, which for this reason is sometimes called simply the random graph. However, the analogous result is not true for uncountable graphs, of which there are many (nonisomorphic) graphs satisfying the above property.
Another model, which generalizes Gilbert's random graph model, is the random dot-product model. A random dot-product graph associates with each vertex a real vector. The probability of an edge uv between any vertices u and v is some function of the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
u • v of their respective vectors.
The network probability matrix
Network Probability Matrix
The network probability matrix describes the probability structure of a network based on the historical presence or absence of edges in a network. For example, individuals in a social network are not connected to other individuals with uniform random probability. The probability structure is much...
models random graphs through edge probabilities, which represent the probability
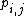that a given edge 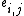exists for a specified time period. This model is extensible to directed and undirected; weighted and unweighted; and static or dynamic graphs.For
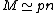the two most widely used models, G(n,M) and G(n,p), are almost interchangeable.Random regular graphs form a special case, with properties that may differ from random graphs in general.
Properties of random graphs
The theory of random graphs studies typical properties of random graphs, those that hold with high probability for graphs drawn from a particular distribution. For example, we might ask for a given value of n and p what the probability is that G(n,p) is connectedConnection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
. In studying such questions, researchers often concentrate on the asymptotic behavior of random graphs—the values that various probabilities converge to as n grows very large. Percolation theory
Percolation theory
In mathematics, percolation theory describes the behavior of connected clusters in a random graph. The applications of percolation theory to materials science and other domains are discussed in the article percolation.-Introduction:...
characterizes the connectedness of random graphs, especially infinitely large ones.
Percolation is related to the robustness of the graph (called also network). Given a random graph of n nodes and an average degree
.
(threshold functions, evolution of G~)
Random graphs are widely used in the probabilistic method
Probabilistic method
The probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the...
, where one
tries to prove the existence of graphs with certain properties. The existence of
a property on a random graph can often imply, via the famous Szemerédi regularity lemma
Szemerédi regularity lemma
In mathematics, the Szemerédi regularity lemma states that every large enough graph can be divided into subsets of about the same size so that the edges between different subsets behave almost randomly. introduced a weaker version of this lemma, restricted to bipartite graphs, in order to prove ...
, the existence of that property on almost all graphs.
Random trees
A random treeRandom tree
In mathematics and computer science, a random tree is a tree or arborescence that is formed by a stochastic process. Types of random trees include:...
is a tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
or arborescence
Arborescence (graph theory)
In graph theory, an arborescence is a directed graph in which, for a vertex u called the root and any other vertex v, there is exactly one directed path from u to v....
that is formed by a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
. Types of random trees include uniform spanning tree, random minimal spanning tree
Random minimal spanning tree
In mathematics, random minimal spanning tree, or random MST, is a model for a random spanning tree of a graph . It might be compared against the uniform spanning tree, a different model for a random tree which has been researched much more extensively...
, random binary tree
Random binary tree
In computer science and probability theory, a random binary tree refers to a binary tree selected at random from some probability distribution on binary trees...
, treap
Treap
In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys...
, rapidly-exploring random tree
Rapidly-exploring random tree
A Rapidly-exploring random tree is a data structure and algorithm designed for efficiently searching nonconvex, high-dimensional search spaces. The tree is constructed in such a way that any sample in the space is added by connecting it to the closest sample already in the tree.RRTs, developed by...
, Brownian tree
Brownian tree
A Brownian tree, whose name is derived from Robert Brown via Brownian motion, is a form of computer art that was briefly popular in the 1990s, when home computers started to have sufficient power to simulate Brownian motion...
, and random forest
Random forest
Random forest is an ensemble classifier that consists of many decision trees and outputs the class that is the mode of the class's output by individual trees. The algorithm for inducing a random forest was developed by Leo Breiman and Adele Cutler, and "Random Forests" is their trademark...
.
Interdependent Graphs
Interdependent graphs or networks is a system of coupled networks where nodes of one or morenetworks depend on nodes in other networks. This dependency is enhanced by the
developments in modern technology. Such dependencies may lead to cascading failures
between the networks and a relatively small damage can lead to a catastrophic
breakdown of the system. Blackouts are a fascinating demonstration of the important
role played by the dependencies between networks. A recent study developed a
framework to study the cascading failures in an interdependent networks system
History
Random graphs were first defined by Paul Erdős and Alfréd RényiAlfréd Rényi
Alfréd Rényi was a Hungarian mathematician who made contributions in combinatorics, graph theory, number theory but mostly in probability theory.-Life:...
in their 1959 paper "On Random Graphs" and independently by Gilbert in his paper "Random graphs".
See also
- Bose–Einstein condensation: a network theory approach
- Cavity methodCavity methodThe Cavity method is a mathematical method due to M. Mezard, Giorgio Parisi and Miguel Angel Virasoro in 1985 to solve some mean field type of models in statistical physics, specially adapted to disordered systems. It has been used to compute properties of ground states in many condensed matter and...
- Complex networks
- Graph theoryGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
- Network scienceNetwork scienceNetwork science is a new and emerging scientific discipline that examines the interconnections among diverse physical or engineered networks, information networks, biological networks, cognitive and semantic networks, and social networks. This field of science seeks to discover common principles,...
- PercolationPercolationIn physics, chemistry and materials science, percolation concerns the movement and filtering of fluids through porous materials...
- Semilinear responseSemilinear Response-Applications:The original motivation for introducing SLRT was the study of mesosopic conductance.The term SLRT has been coined inwhere it has been applied to the calculation of energy absorption by metallic grains....