
Random minimal spanning tree
Encyclopedia
In mathematics
, random minimal spanning tree, or random MST, is a model (actually two related models) for a random spanning tree
of a graph (see also minimal spanning tree). It might be compared against the uniform spanning tree, a different model for a random tree which has been researched much more extensively. For additional types of random tree, see random tree
.
. To define the random MST on G, make G into a weighted graph by choosing weights randomly, uniformly
between 0 and 1 independently
for each edge. Now pick the MST from this weighted graph i.e. the spanning tree
with the lowest total weight. Almost surely
, there would be only one i.e. there would be not be two distinct spanning trees with identical total weight. This tree (denote it by T) is also a spanning tree for the unweighted graph G. This is the random MST.
The most important case, and the one that will be discussed in this page, is that the graph G is a part of a lattice in Euclidean space
. For example, take the vertex set to be all the points in the plane
(x,y) with x and y both integer
s between 1 and some N. Make this into a graph by putting an edge between every two points with distance 1. This graph will be denoted by
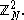
Mainly we will think about N as large and be interested in asymptotic properties as N goes to infinity.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, random minimal spanning tree, or random MST, is a model (actually two related models) for a random spanning tree
Spanning tree
Spanning tree can refer to:* Spanning tree , a tree which contains every vertex of a more general graph* Spanning tree protocol, a protocol for finding spanning trees in bridged networks...
of a graph (see also minimal spanning tree). It might be compared against the uniform spanning tree, a different model for a random tree which has been researched much more extensively. For additional types of random tree, see random tree
Random tree
In mathematics and computer science, a random tree is a tree or arborescence that is formed by a stochastic process. Types of random trees include:...
.
First model
Let G be a finite connected graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
. To define the random MST on G, make G into a weighted graph by choosing weights randomly, uniformly
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
between 0 and 1 independently
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
for each edge. Now pick the MST from this weighted graph i.e. the spanning tree
Spanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
with the lowest total weight. Almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
, there would be only one i.e. there would be not be two distinct spanning trees with identical total weight. This tree (denote it by T) is also a spanning tree for the unweighted graph G. This is the random MST.
The most important case, and the one that will be discussed in this page, is that the graph G is a part of a lattice in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. For example, take the vertex set to be all the points in the plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
(x,y) with x and y both integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s between 1 and some N. Make this into a graph by putting an edge between every two points with distance 1. This graph will be denoted by
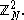
Mainly we will think about N as large and be interested in asymptotic properties as N goes to infinity.

