Erdos–Rényi model
Encyclopedia
In graph theory
, the Erdős–Rényi model, named for Paul Erdős
and Alfréd Rényi
, is either of two models for generating random graph
s, including one that sets an edge between each pair of nodes with equal probability, independently
of the other edges. It can be used in the probabilistic method
to prove the existence of graphs satisfying various properties, or to provide a rigorous definition of what it means for a property to hold for almost all
graphs.
The behavior of random graphs are often studied in the case where n, the number of vertices, tends to infinity. Although p and M can be fixed in this case, they can also be functions depending on n. For example, the statement "almost every graph in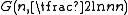
is connected" means "as n tends to infinity, the probability that a graph on n vertices with edge probability 
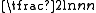is connected tends to 1".
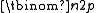, and by the law of large numbers
any graph in G(n,p) will almost surely have approximately this many edges (provided the expected number of edges tends to infinity). Therefore a rough heuristic is that if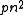
tends to infinity, then G(n,p) should behave similarly to G(n,M) with 
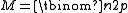as n increases.
For many graph properties, this is the case. If P is any graph property which is monotone
with respect to the subgraph ordering (meaning that if A is a subgraph of B and A satisfies P, then B will satisfy P as well), then the statements "P holds for almost all graphs in G(n, p)" and "P holds for almost all graphs in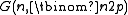
" are equivalent (provided 
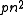tends to infinity). For example, this holds if P is the property of being connected
, or if P is the property of containing a Hamiltonian cycle
. However, this will not necessarily hold for non-monotone properties (e.g. the property of having an even number of edges).
In practice, the G(n, p) model is the one more commonly used today, in part due to the ease of analysis allowed by the independence of the edges.
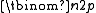edges. The distribution of the degree of any particular vertex is binomial:
where n is the total number of vertices in the graph. Since
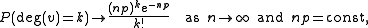
this distribution is Poisson
for large n and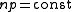
.
In a 1960 paper, Erdős and Rényi described the behavior of G(n, p) very precisely for various values of p. Their results included that:
Thus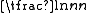
is a sharp threshold for the connectedness of G(n, p).
Further properties of the graph can be described almost precisely as n tends to infinity. For example, there is a k(n) (approximately equal to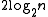
) such that the largest clique
in G(n, 0.5) has almost surely either size k(n) or k(n) + 1.
Thus, even though finding the size of the largest clique in a graph is NP-complete
, the size of the largest clique in a "typical" graph (according to this model) is very well understood.
one examines a finite or infinite graph and removes edges randomly. Thus the Erdős–Rényi process is in fact percolation on the complete graph
. As percolation theory has much of its roots in physics
, much of the research done was on the lattices
in Euclidean spaces. The transition at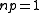
from giant component to small component has analogs for these graphs, but for lattices the transition point is difficult to determine. Physicists often refer to study of the complete graph as a mean field theory
. Thus the Erdős–Rényi process is the mean-field case of percolation.
Some significant work was also done on percolation on random graphs. From a physicist's point of view this would still be a mean-field model, so the justification of the research is often formulated in terms of the robustness of the graph, viewed as a communication network. Given a random graph of n >> 1 nodes with an average degree <k>. Remove randomly a fraction 1 − p' of nodes and leave only a fraction p' from the network. There exists a critical percolation threshold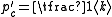 
below which the network becomes fragmented while above 
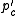a giant connected component of order n exists. The relative size of the giant component, 
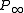, is given by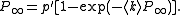
.
A model for interacting ER networks was developed recently by Buldyrev et al..
in a 1959 paper which studied the connectivity threshold mentioned above. The G(n, M) model was introduced by Erdős and Rényi in their 1959 paper. As with Gilbert, their first investigations were as to the connectivity of G(n, M), with the more detailed analysis following in 1960.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Erdős–Rényi model, named for Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
and Alfréd Rényi
Alfréd Rényi
Alfréd Rényi was a Hungarian mathematician who made contributions in combinatorics, graph theory, number theory but mostly in probability theory.-Life:...
, is either of two models for generating random graph
Random graph
In mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
s, including one that sets an edge between each pair of nodes with equal probability, independently
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
of the other edges. It can be used in the probabilistic method
Probabilistic method
The probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the...
to prove the existence of graphs satisfying various properties, or to provide a rigorous definition of what it means for a property to hold for almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
graphs.
Definition
There are two closely related variants of the Erdős–Rényi (ER) random graph model.- In the G(n, M) model, a graph is chosen uniformly at random from the collection of all graphs which have n nodes and M edges. For example, in the G(3, 2) model, each of the three possible graphs on three vertices and two edges are included with probability 1/3.
- In the G(n, p) model, a graph is constructed by connecting nodes randomly. Each edge is included in the graph with probability p independent from every other edge. Equivalently, all graphs with n nodes and M edges have equal probability of
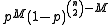. The parameter p in this model can be thought of as a weighting function; as p increases from 0 to 1, the model becomes more and more likely to include graphs with more edges and less and less likely to include graphs with fewer edges. In particular, the case p = 0.5 corresponds to the case where all 
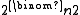graphs on n vertices are chosen with equal probability.
The behavior of random graphs are often studied in the case where n, the number of vertices, tends to infinity. Although p and M can be fixed in this case, they can also be functions depending on n. For example, the statement "almost every graph in
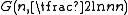is connected" means "as n tends to infinity, the probability that a graph on n vertices with edge probability 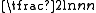is connected tends to 1".Comparison between the two models
The expected number of edges in G(n,p) is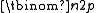, and by the law of large numbersLaw of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
any graph in G(n,p) will almost surely have approximately this many edges (provided the expected number of edges tends to infinity). Therefore a rough heuristic is that if
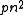tends to infinity, then G(n,p) should behave similarly to G(n,M) with 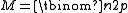as n increases.For many graph properties, this is the case. If P is any graph property which is monotone
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
with respect to the subgraph ordering (meaning that if A is a subgraph of B and A satisfies P, then B will satisfy P as well), then the statements "P holds for almost all graphs in G(n, p)" and "P holds for almost all graphs in
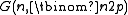" are equivalent (provided 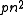tends to infinity). For example, this holds if P is the property of being connectedConnectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
, or if P is the property of containing a Hamiltonian cycle
Hamiltonian path
In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle in an undirected graph that visits each vertex exactly once and also returns to the starting vertex...
. However, this will not necessarily hold for non-monotone properties (e.g. the property of having an even number of edges).
In practice, the G(n, p) model is the one more commonly used today, in part due to the ease of analysis allowed by the independence of the edges.
Properties of G(n, p)
With the notation above, a graph in G(n, p) has on average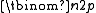 edges. The distribution of the degree of any particular vertex is binomial:
where n is the total number of vertices in the graph. Since
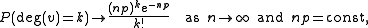
this distribution is Poisson
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
for large n and
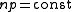.In a 1960 paper, Erdős and Rényi described the behavior of G(n, p) very precisely for various values of p. Their results included that:
- If
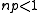, then a graph in G(n, p) will almost surely have no connected components of size larger than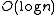 
- If
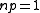, then a graph in G(n, p) will almost surely have a largest component whose size is of order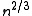 
- If
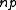tends to a constant c > 1, then a graph in G(n, p) will almost surely have a unique giant componentGiant componentIn network theory, a giant component is a connected component of a given random graph that contains a constant fraction of the entire graph's vertices....
containing a positive fraction of the vertices. No other component will contain more than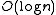
vertices.
- If
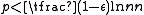, then a graph in G(n, p) will almost surely contain isolated vertices, and thus be disconnected. - If
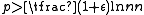, then a graph in G(n, p) will almost surely be connected.
Thus
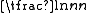is a sharp threshold for the connectedness of G(n, p).Further properties of the graph can be described almost precisely as n tends to infinity. For example, there is a k(n) (approximately equal to
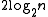) such that the largest cliqueClique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
in G(n, 0.5) has almost surely either size k(n) or k(n) + 1.
Thus, even though finding the size of the largest clique in a graph is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
, the size of the largest clique in a "typical" graph (according to this model) is very well understood.
Relation to percolation
In percolation theoryPercolation theory
In mathematics, percolation theory describes the behavior of connected clusters in a random graph. The applications of percolation theory to materials science and other domains are discussed in the article percolation.-Introduction:...
one examines a finite or infinite graph and removes edges randomly. Thus the Erdős–Rényi process is in fact percolation on the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
. As percolation theory has much of its roots in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, much of the research done was on the lattices
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
in Euclidean spaces. The transition at
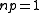from giant component to small component has analogs for these graphs, but for lattices the transition point is difficult to determine. Physicists often refer to study of the complete graph as a mean field theoryMean field theory
Mean field theory is a method to analyse physical systems with multiple bodies. A many-body system with interactions is generally very difficult to solve exactly, except for extremely simple cases . The n-body system is replaced by a 1-body problem with a chosen good external field...
. Thus the Erdős–Rényi process is the mean-field case of percolation.
Some significant work was also done on percolation on random graphs. From a physicist's point of view this would still be a mean-field model, so the justification of the research is often formulated in terms of the robustness of the graph, viewed as a communication network. Given a random graph of n >> 1 nodes with an average degree <k>. Remove randomly a fraction 1 − p
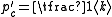below which the network becomes fragmented while above 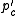a giant connected component of order n exists. The relative size of the giant component, 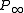, is given by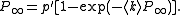Caveats
Both of the two major assumptions of the G(n, p) model (that edges are independent and that each edge is equally likely) may be inappropriate for modeling real-life phenomena. In particular, an Erdős–Rényi graph does not have heavy tails, as is the case in many real networks. Moreover, it has low clustering, unlike many social networks. For popular modeling alternatives, see Barabási–Albert model and Watts and Strogatz modelWatts and Strogatz model
The Watts and Strogatz model is a random graph generation model that produces graphs with small-world properties, including short average path lengths and high clustering. It was proposed by Duncan J. Watts and Steven Strogatz in their joint 1998 Nature paper...
.
A model for interacting ER networks was developed recently by Buldyrev et al..
History
The G(n, p) model was first introduced by Edgar GilbertEdgar Gilbert
Edgar Nelson Gilbert was an American mathematician and coding theorist, a longtime researcher at Bell Laboratories whose accomplishments include the Gilbert–Varshamov bound in coding theory, the Gilbert–Elliott model of bursty errors in signal transmission, and the Erdős–Rényi model for random...
in a 1959 paper which studied the connectivity threshold mentioned above. The G(n, M) model was introduced by Erdős and Rényi in their 1959 paper. As with Gilbert, their first investigations were as to the connectivity of G(n, M), with the more detailed analysis following in 1960.
See also
- Rado graphRado graphIn the mathematical field of graph theory, the Rado graph, also known as the random graph or the Erdős–Renyi graph, is the unique countable graph R such that for any finite graph G and any vertex v of G, any embedding of G − v as an induced subgraph of R can be extended to an...
, the graph formed by extending the G(n, p) model to graphs with a countably infinite number of vertices. Unlike in the finite case, the result of this infinite random process is always (with probability 1Almost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
) the same graph, up to isomorphism.